アナログコンピュータのアプリケーション
自作のアナログコンピュータを使って様々な問題を解析し、その過程と結果を記録しています。
注意
スケーリングに関しては、特記なき限り以下の表記と設定を使用する。
- 原従属変数yに対する演算変数を\(Y\)、電圧換算係数を\(a_{Y}\)とする。
- 演算時間を\(\tau\)、その換算係数を\(a_\tau\)、陽に現れる独立変数に対する演算変数を\(T\)、その換算係数を\(a_T\)とする。
- マシンユニットは10Vとする。
詳細は演算の理論を参照。
|
|
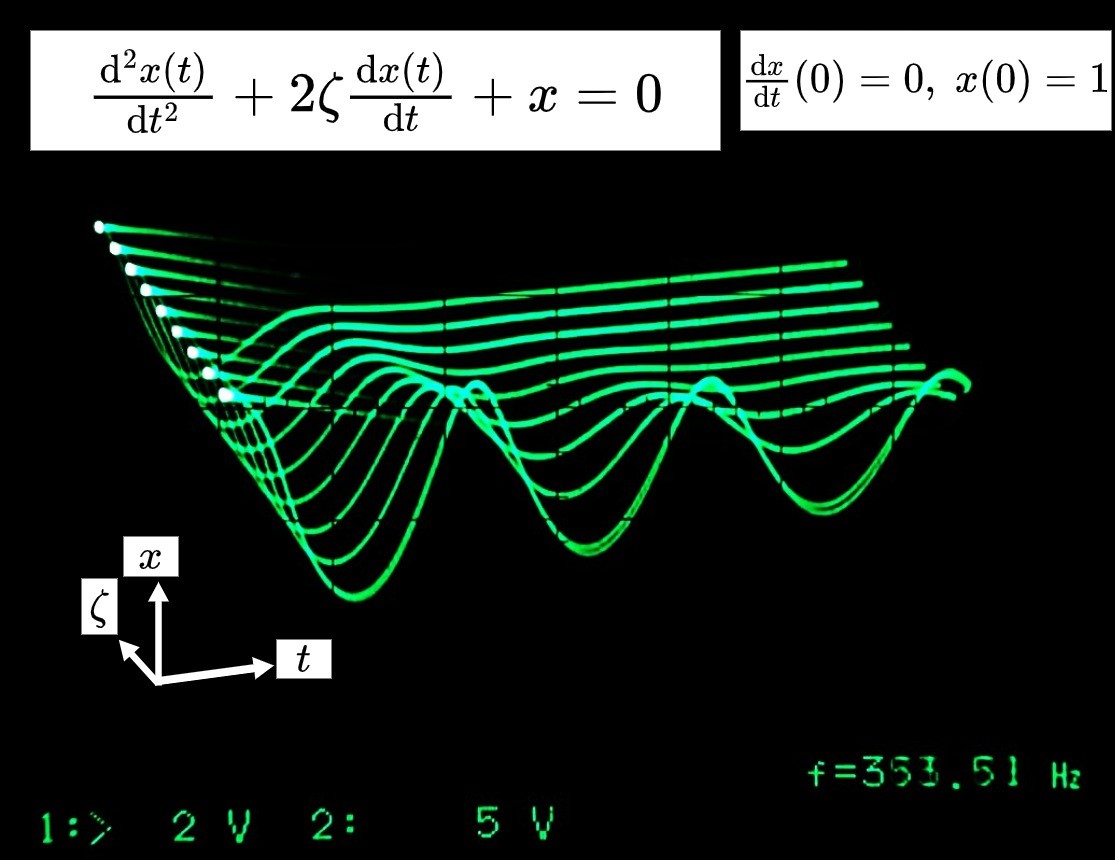
速度に比例する抵抗力が働く線形振動子マス-ばね-ダンパ系のように、減衰項を有する2階線形常微分方程式で表される力学系の挙動を確かめる |
|
|
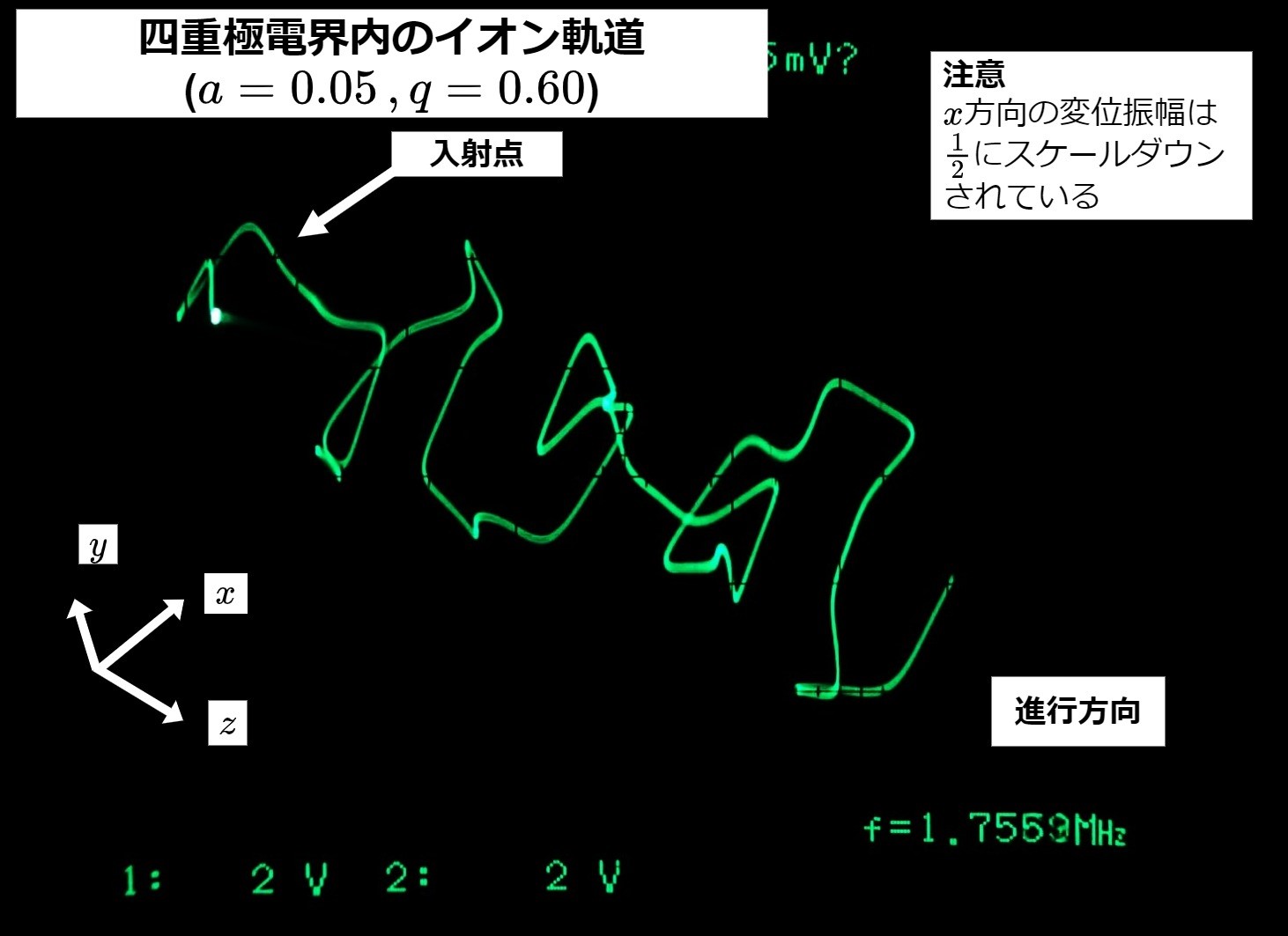
四重極電界内におけるイオン軌道四重極質量分析計(QMS)の質量分離部におけるイオンの運動方程式は、Mathieuの微分方程式と呼ばれる形になる |
|
|
2重振り子のシミュレーション非線形常微分方程式で表される2質点カオス力学系のふるまいを可視化する。 |
|
|
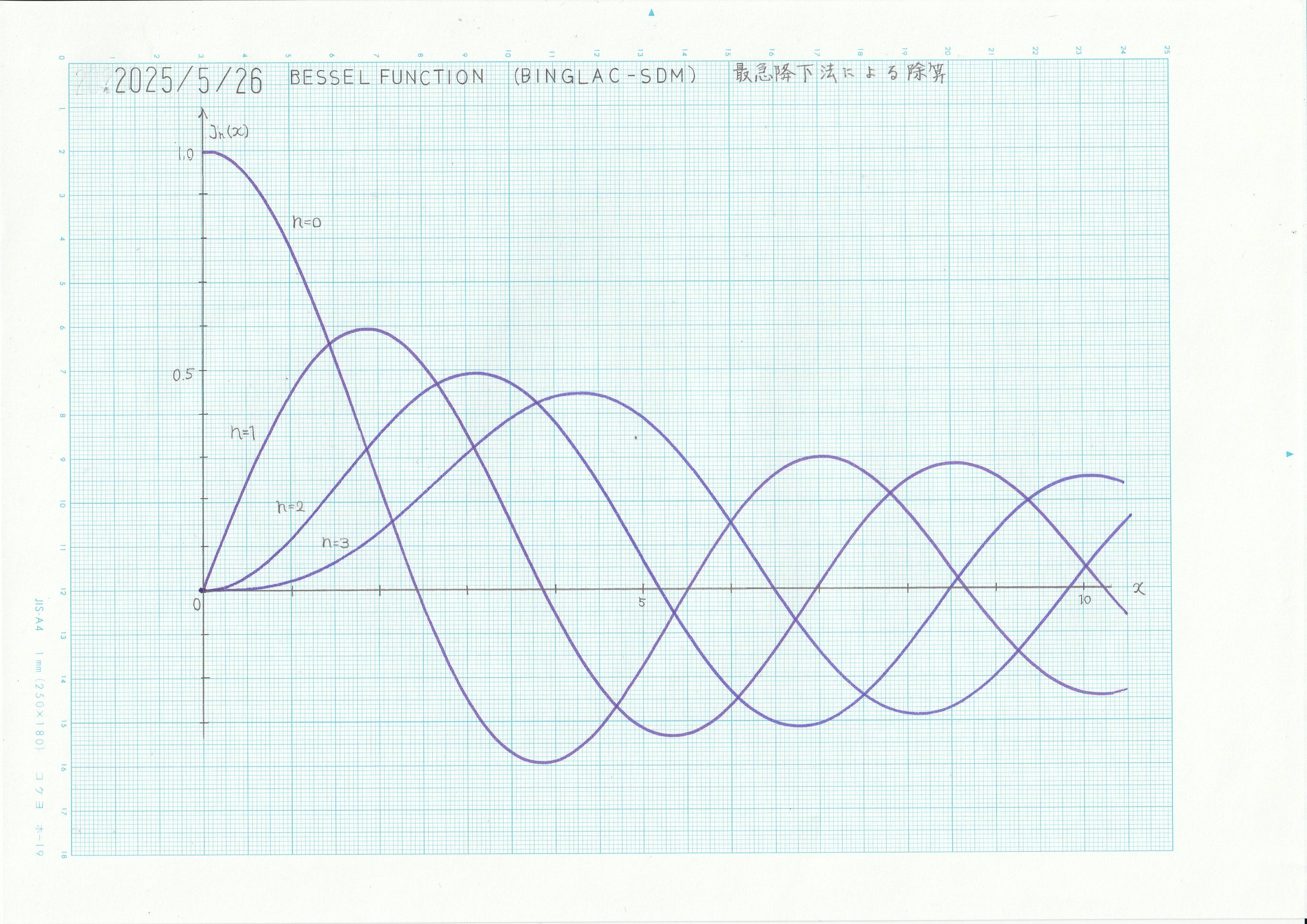
第1種ベッセル関数ベッセルの微分方程式は、円筒座標系においてラプラス方程式やヘルムホルツ方程式を変数分離する際に登場する。 |
|
|
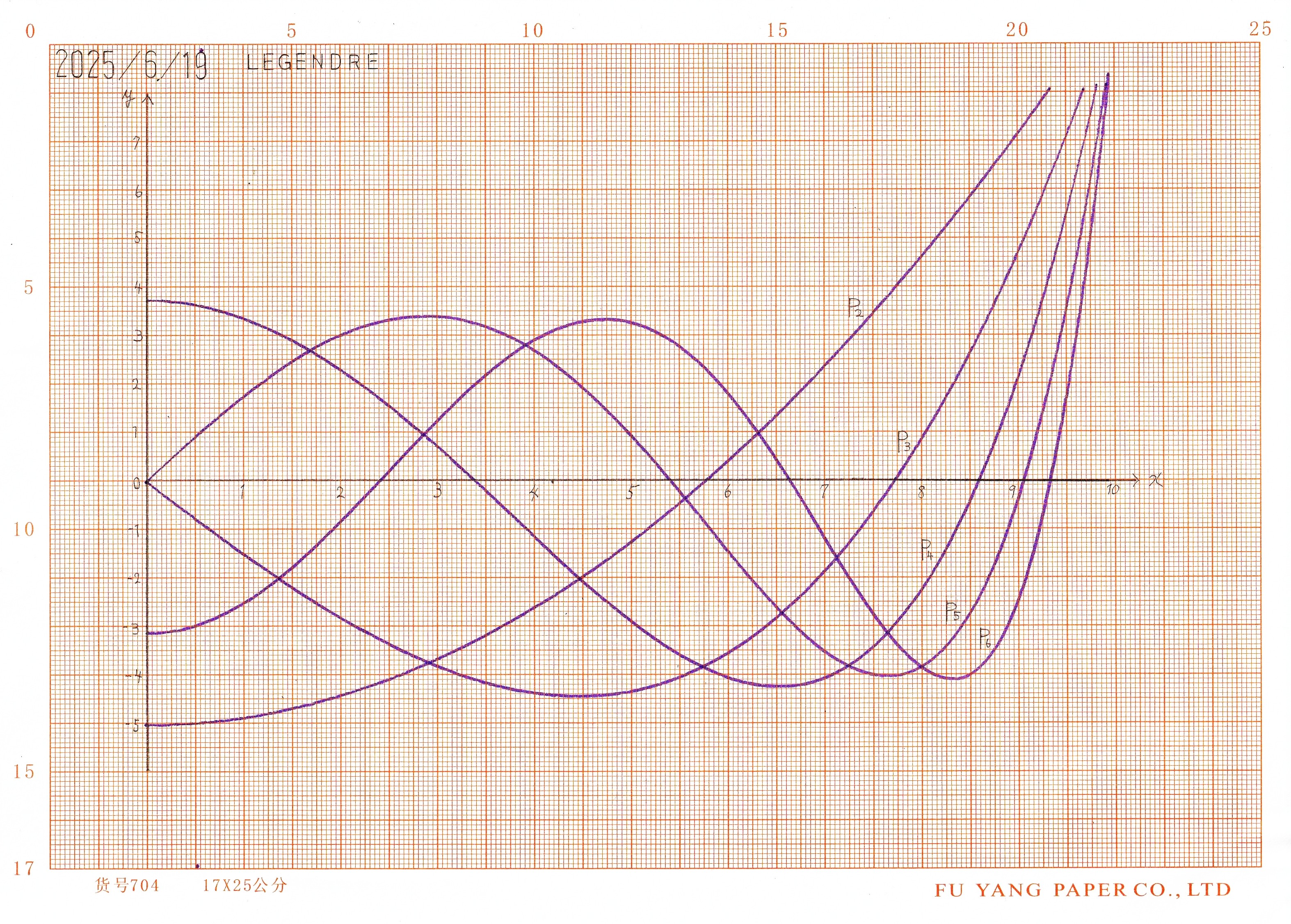
ルジャンドルの微分方程式媒介変数法(Hausnerの方法)により特異点を除去して演算する。 |
|
|
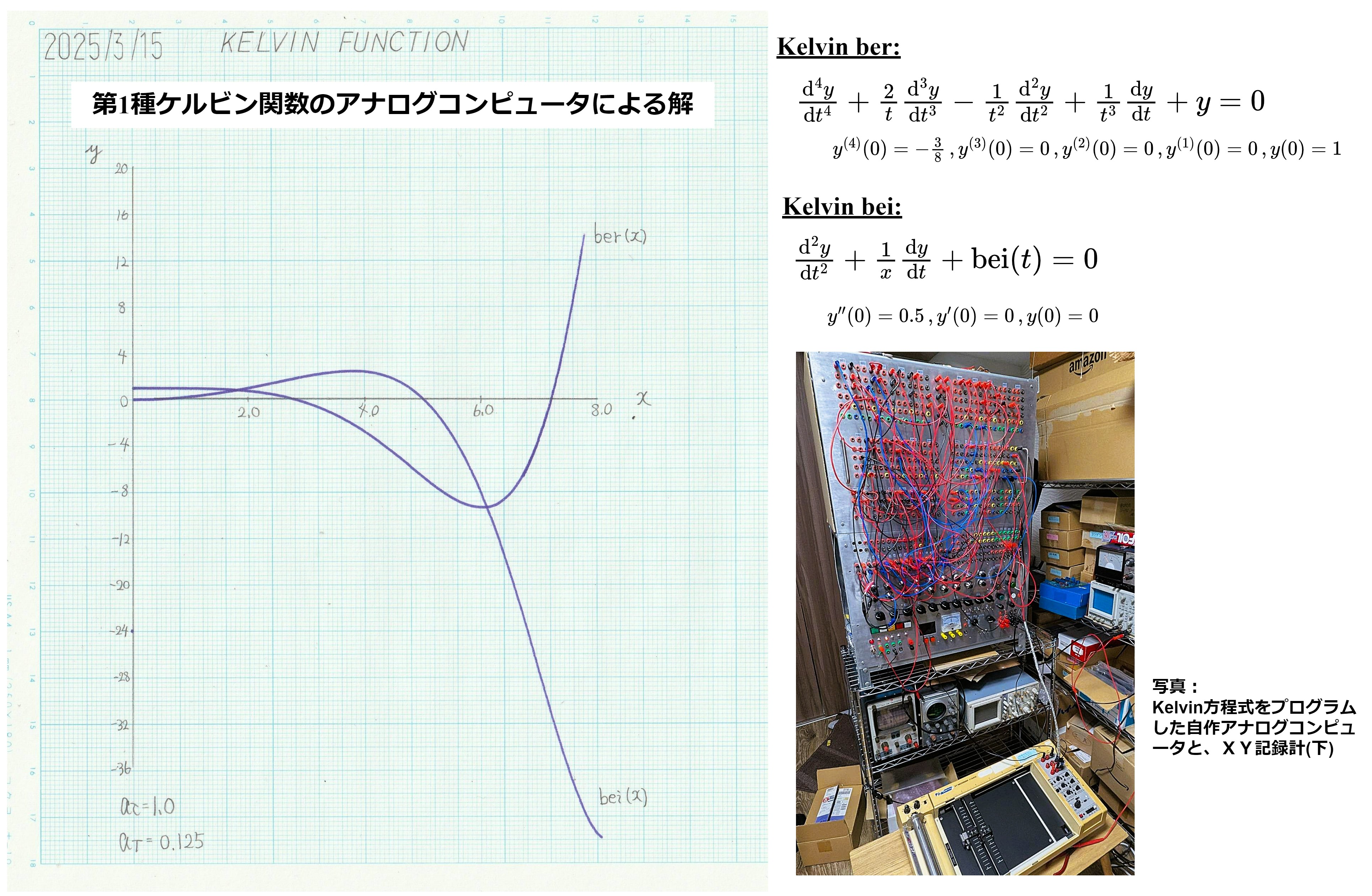
第1種ケルビン関数係数に極がある4階常微分方程式を解き、ber(x)・bei(x)のグラフを得る |
|
|
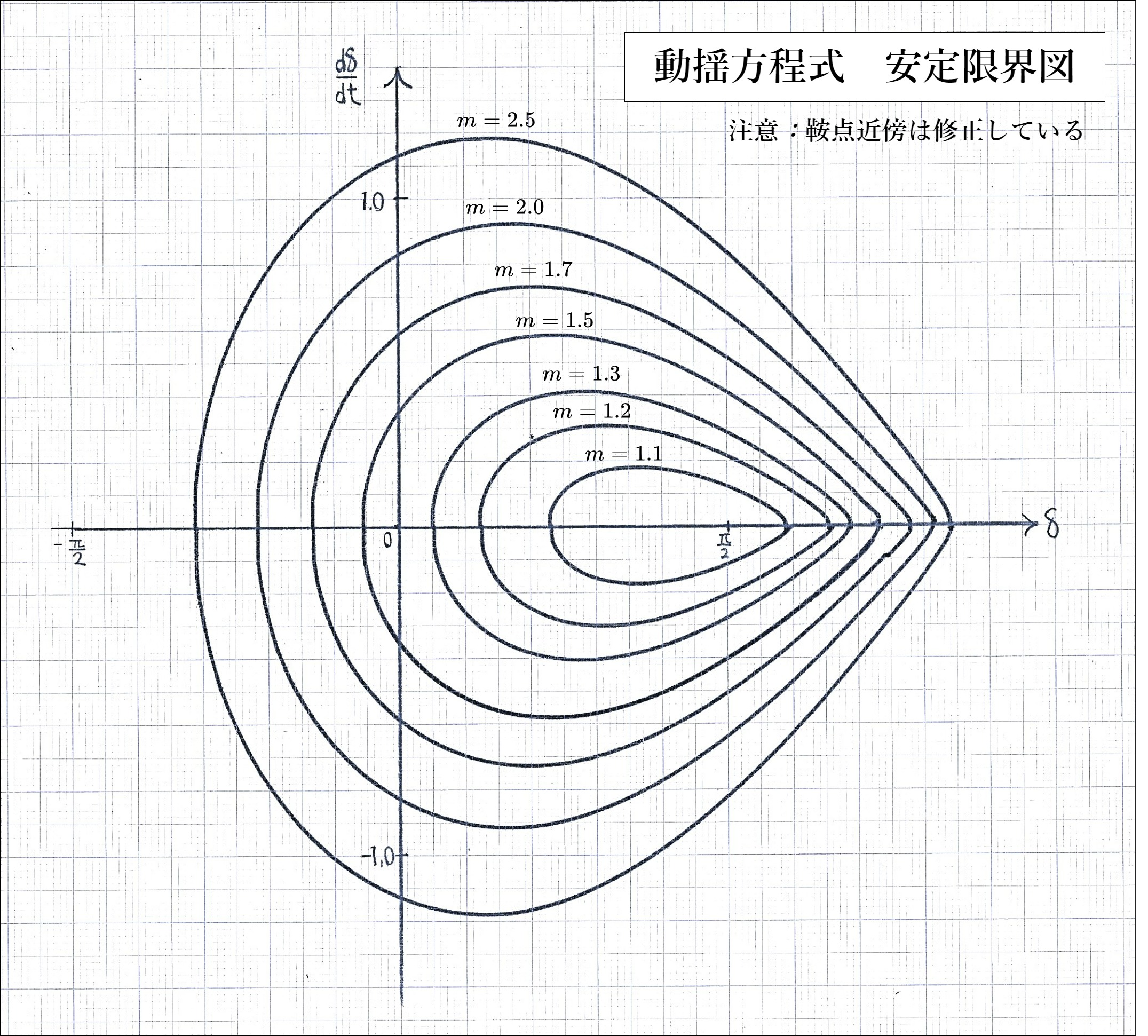
一機無限大母線系統の過渡安定度電力動揺方程式をアナログコンピュータで解く |
|
|
水素原子のシュレディンガー方程式動径方向の波動関数・分布関数のグラフをアナログコンピュータで求める |
|
|
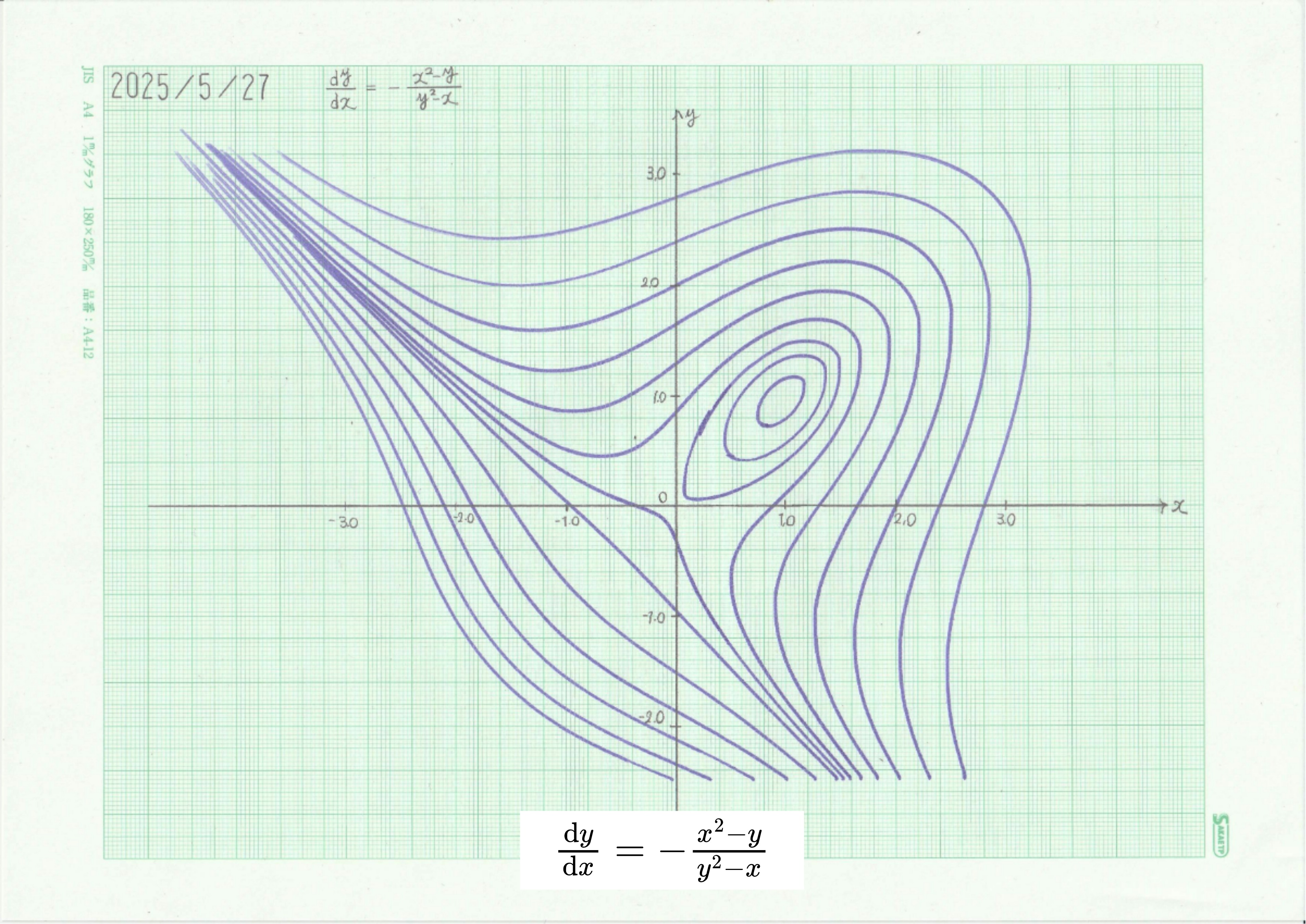
dy/dx=P(x,y)/Q(x,y)で表される微分方程式演算独立変数として媒介変数 \(t\) を導入し、連立微分方程式に直すことで簡単に解が得られる。相平面上での積分曲線を描き、安定性についても考察する。 |
|
|
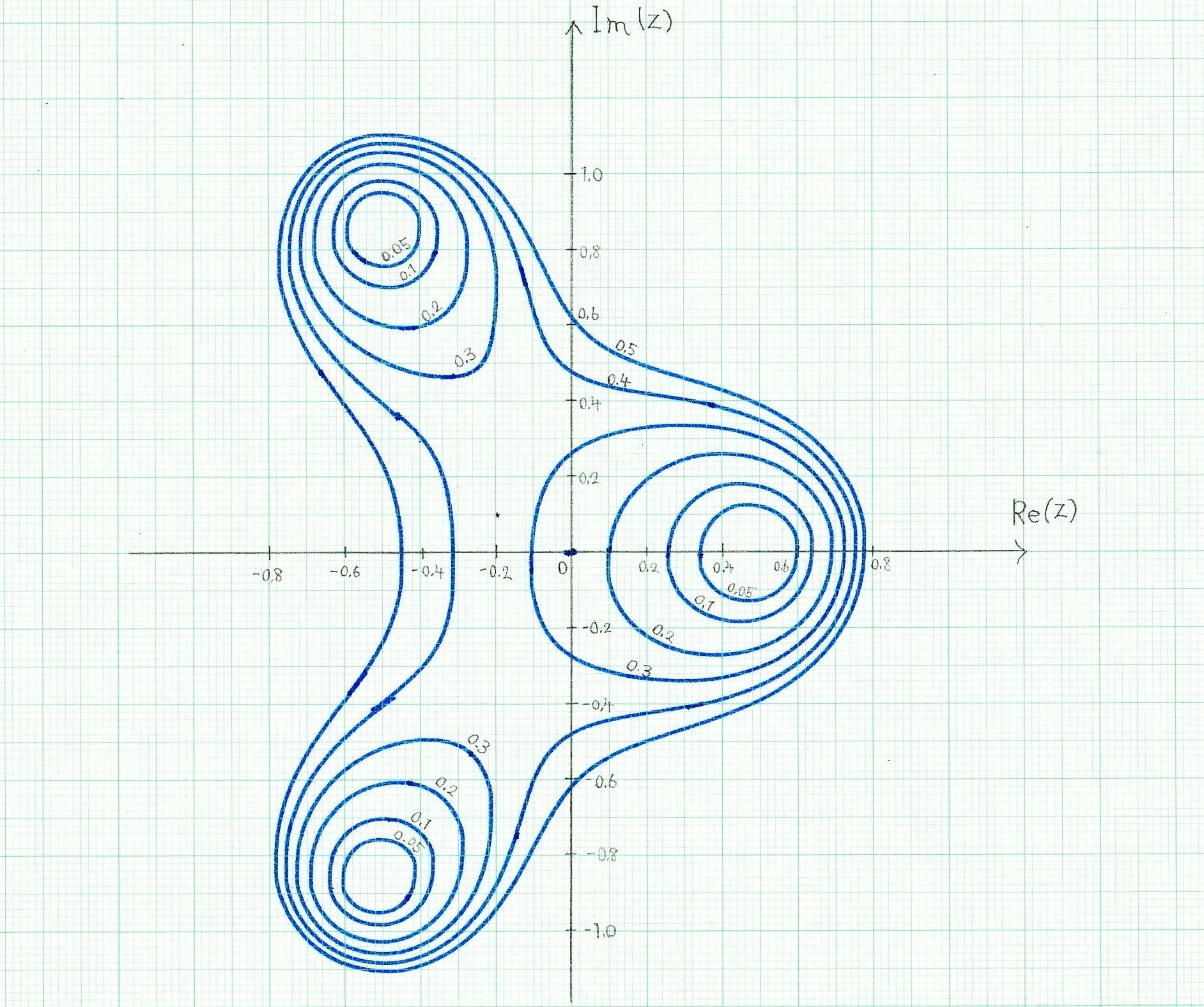
複素関数と等位線・高次多項式の複素根複素関数の取り扱いと、複素求根の手法(アイソグラフのしくみ)を説明する。 |
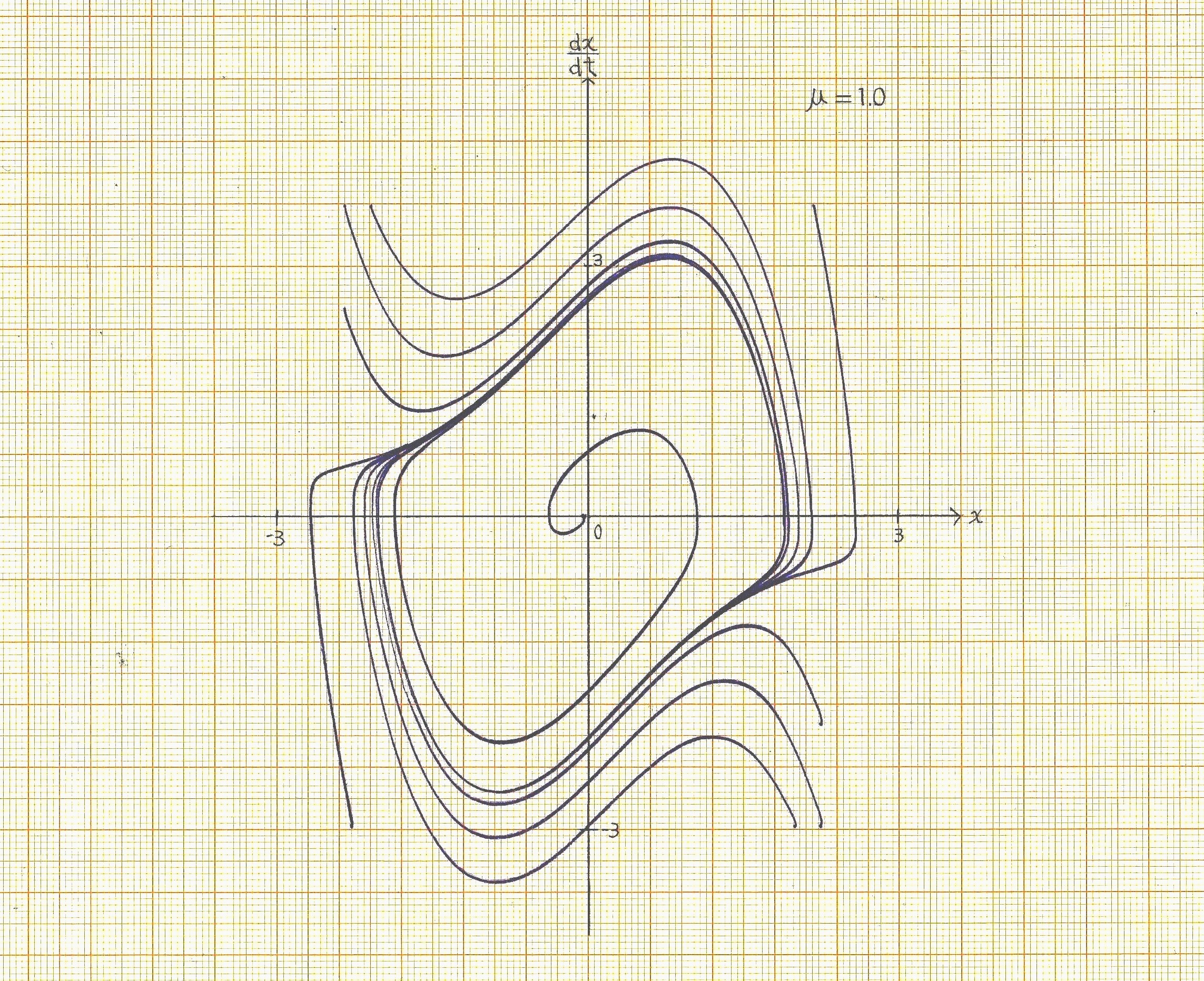 |
ファンデルポール方程式自励振動系のシミュレーション |
|
|
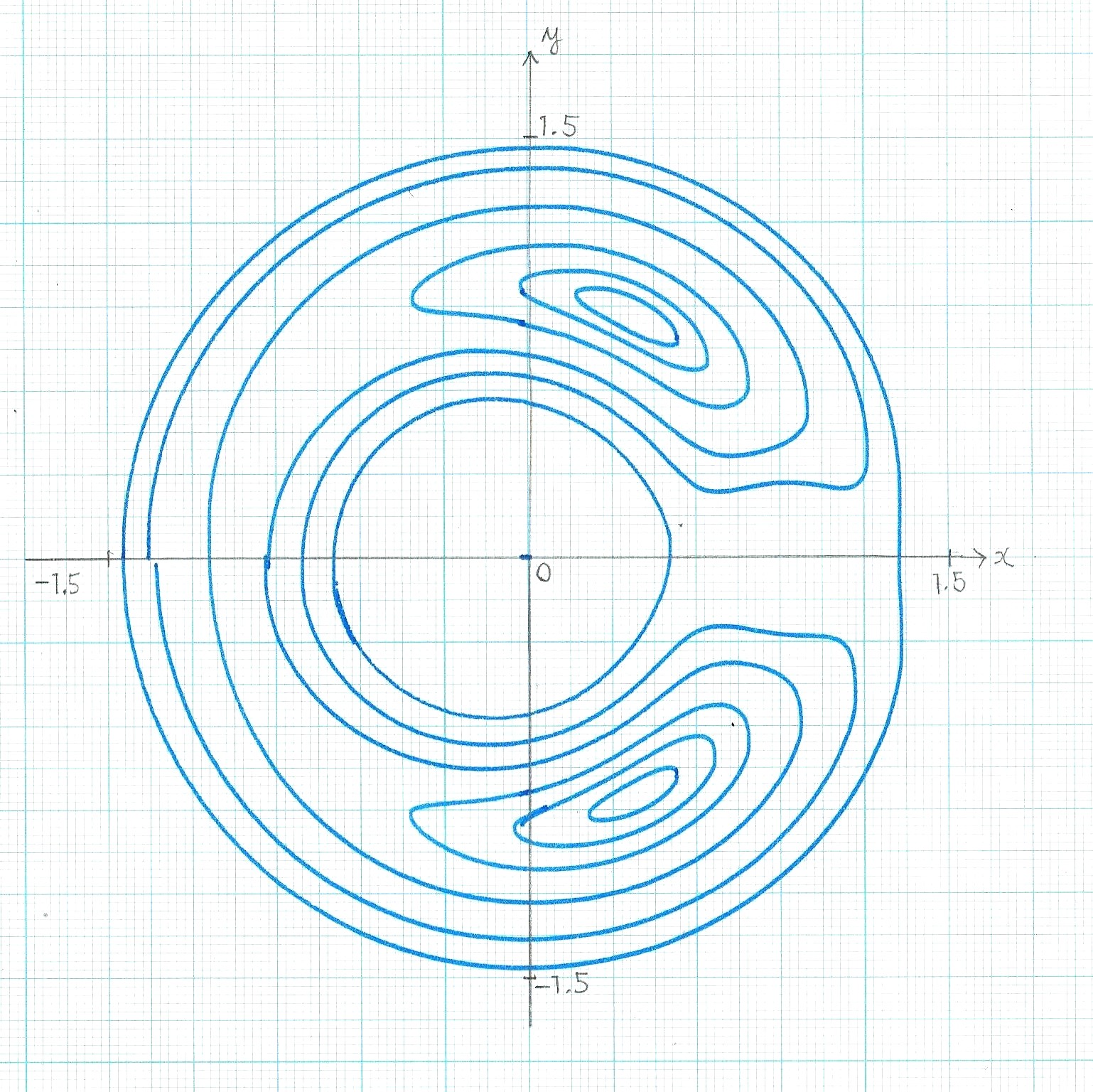
円制限3体問題円制限3体問題をアナログコンピュータ解く。陰伏代数方程式で表されるゼロ速度曲線も描出する。 |
|
|
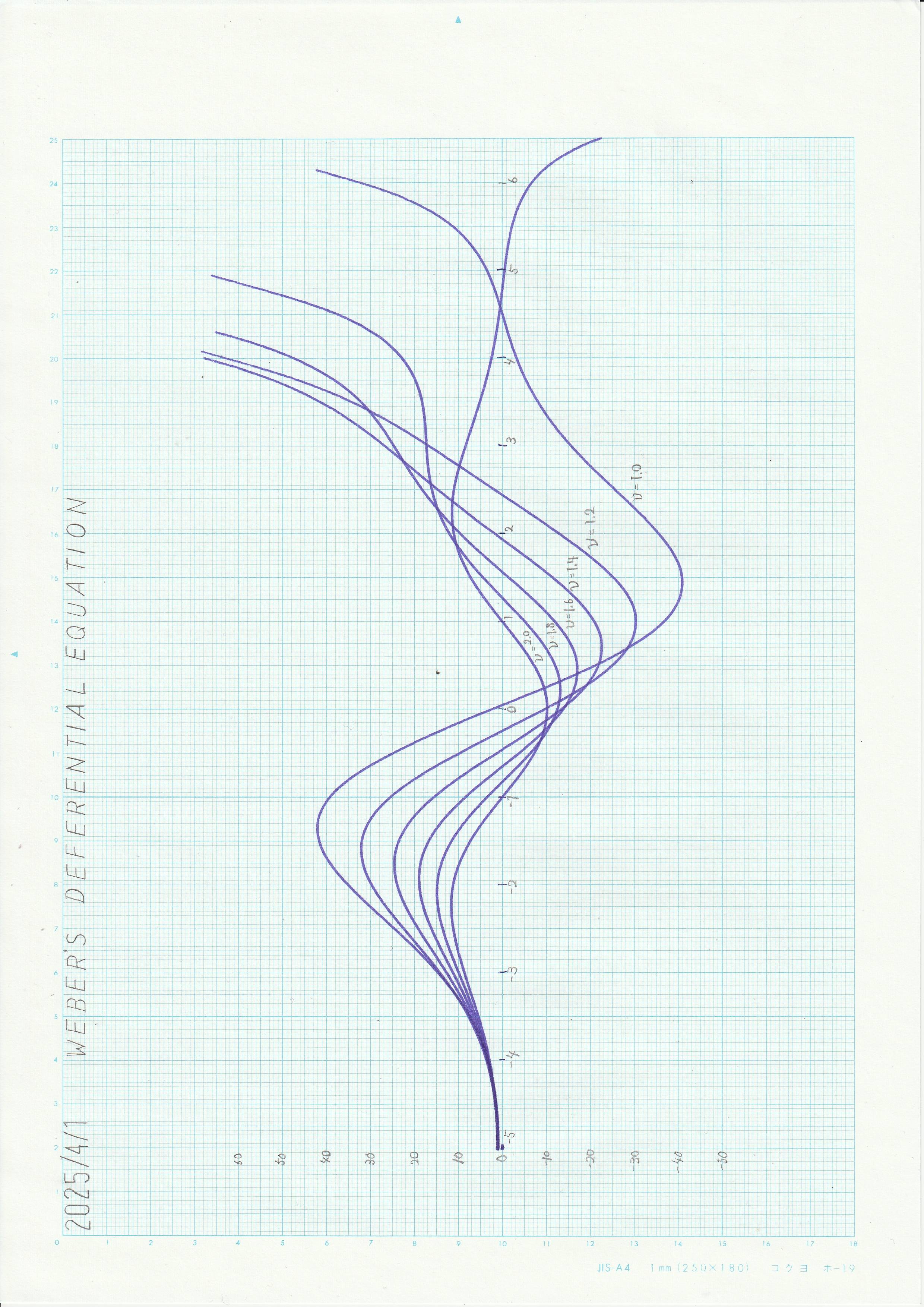
Weberの微分方程式と放物柱関数Weberの微分方程式は、放物柱座標でのヘルムホルツ方程式を変数分離する際に登場する |
|
|
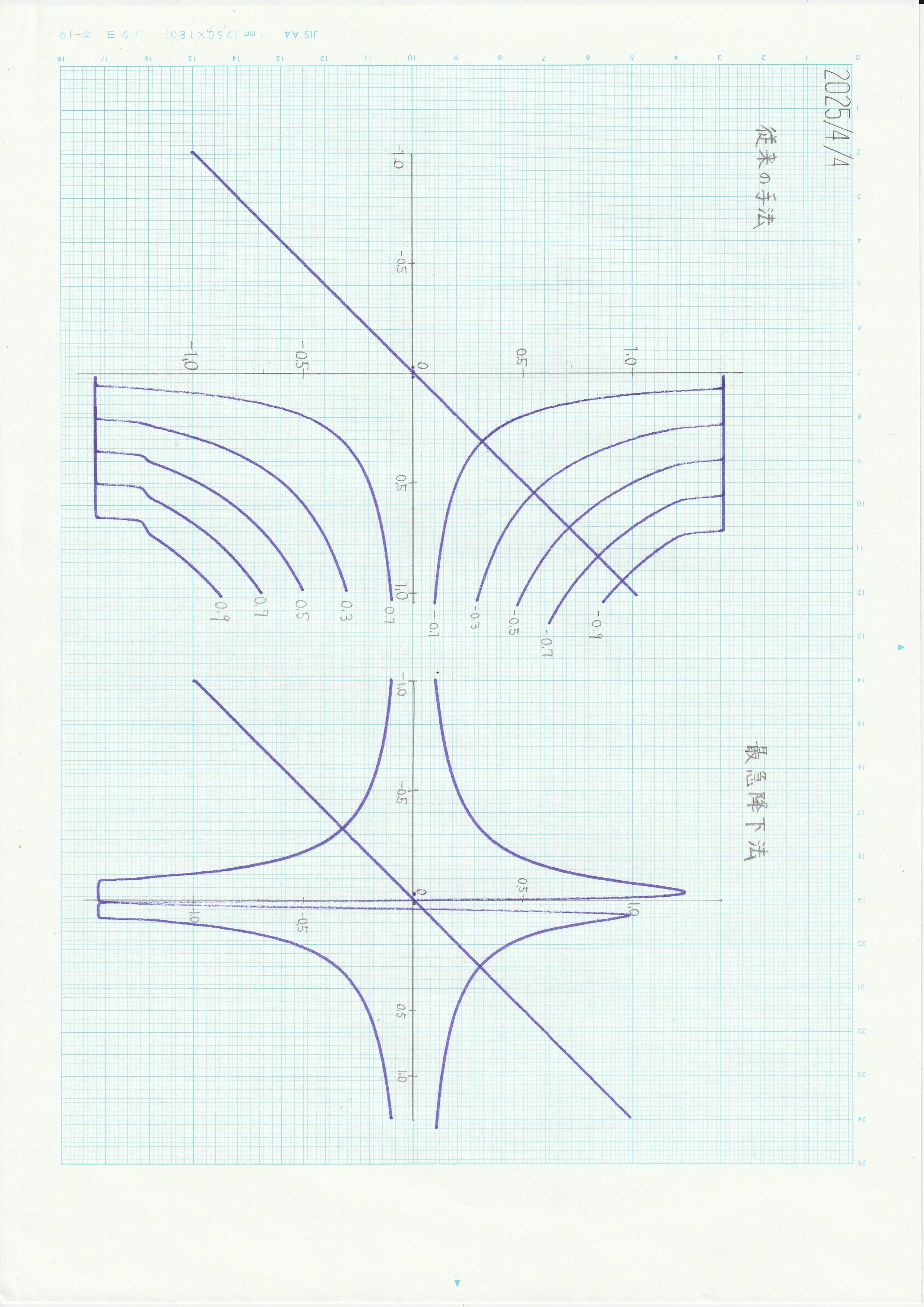
最急降下法による除算係数に極のある式(tan関数やsinc関数など)を陽表的に表すことができる。 |
|
|
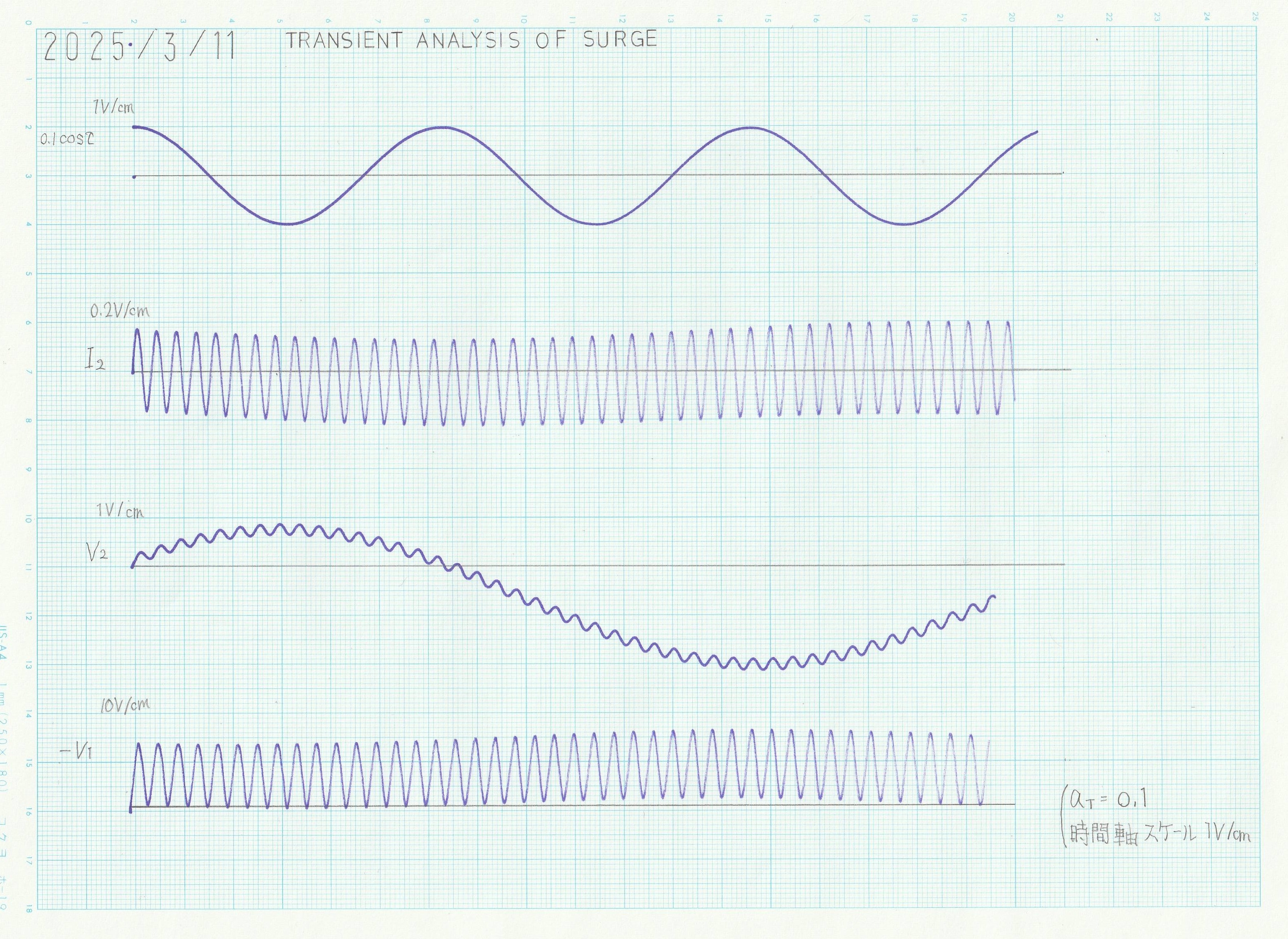
送電系統における開閉サージの過渡解析連立常微分方程式で表現される連成線形振動の影響を調べる |
|
|
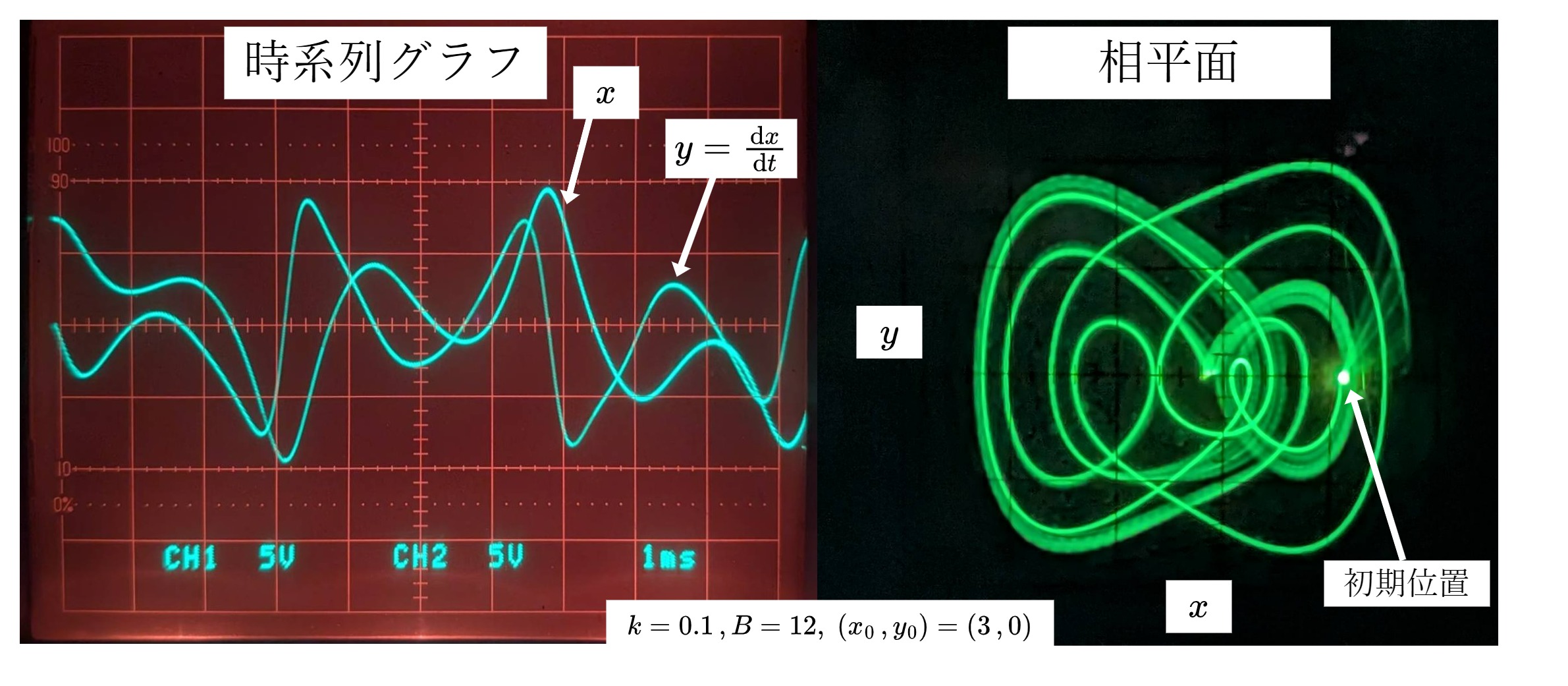
非線形インダクタンスを含む共振回路いわゆる"鉄共振回路"である。周期外力と非線形項により相平面にカオスアトラクタ(上田アトラクタ・ジャパニーズアトラクタ)が生じる |
|
|
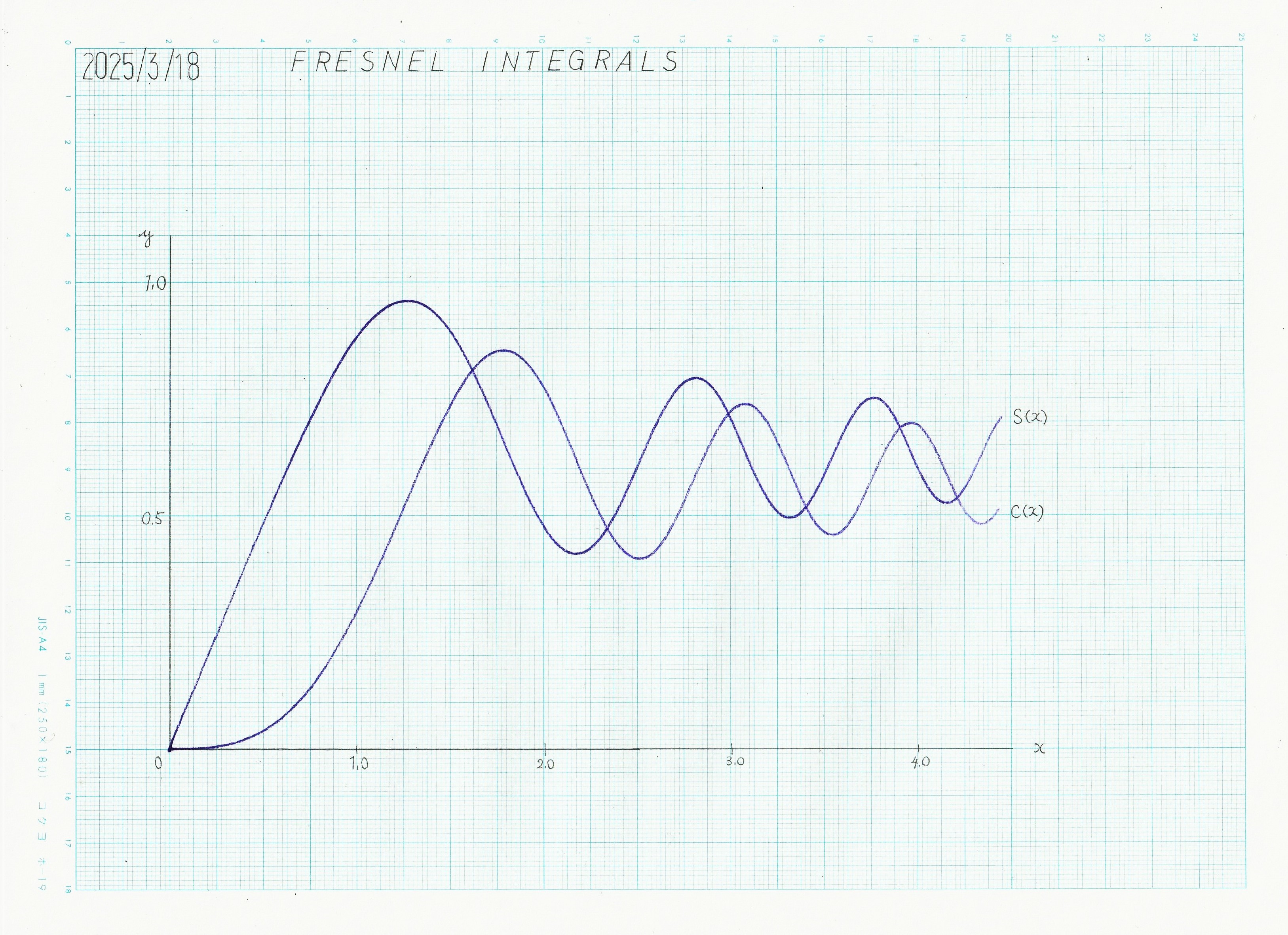
フレネル回折のシミュレーション解析的には実行不能なフレネル積分をアナログコンピュータで演算する (フレネル回折の方は失敗) |
|
|
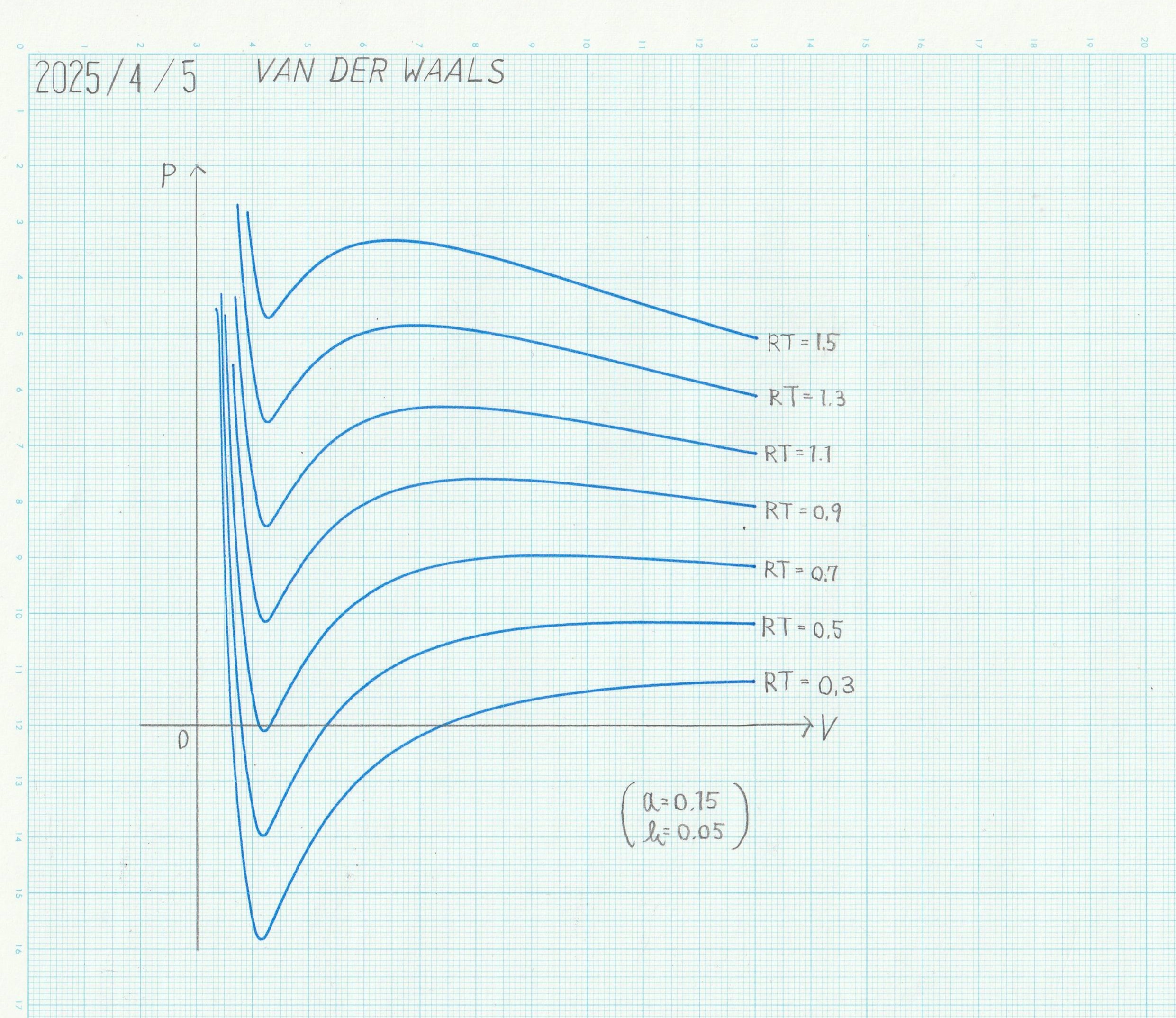
ファンデルワールスの式理想気体の状態方程式を例に、代数方程式を陰関数法で解く方法を解説する。 |
|
|
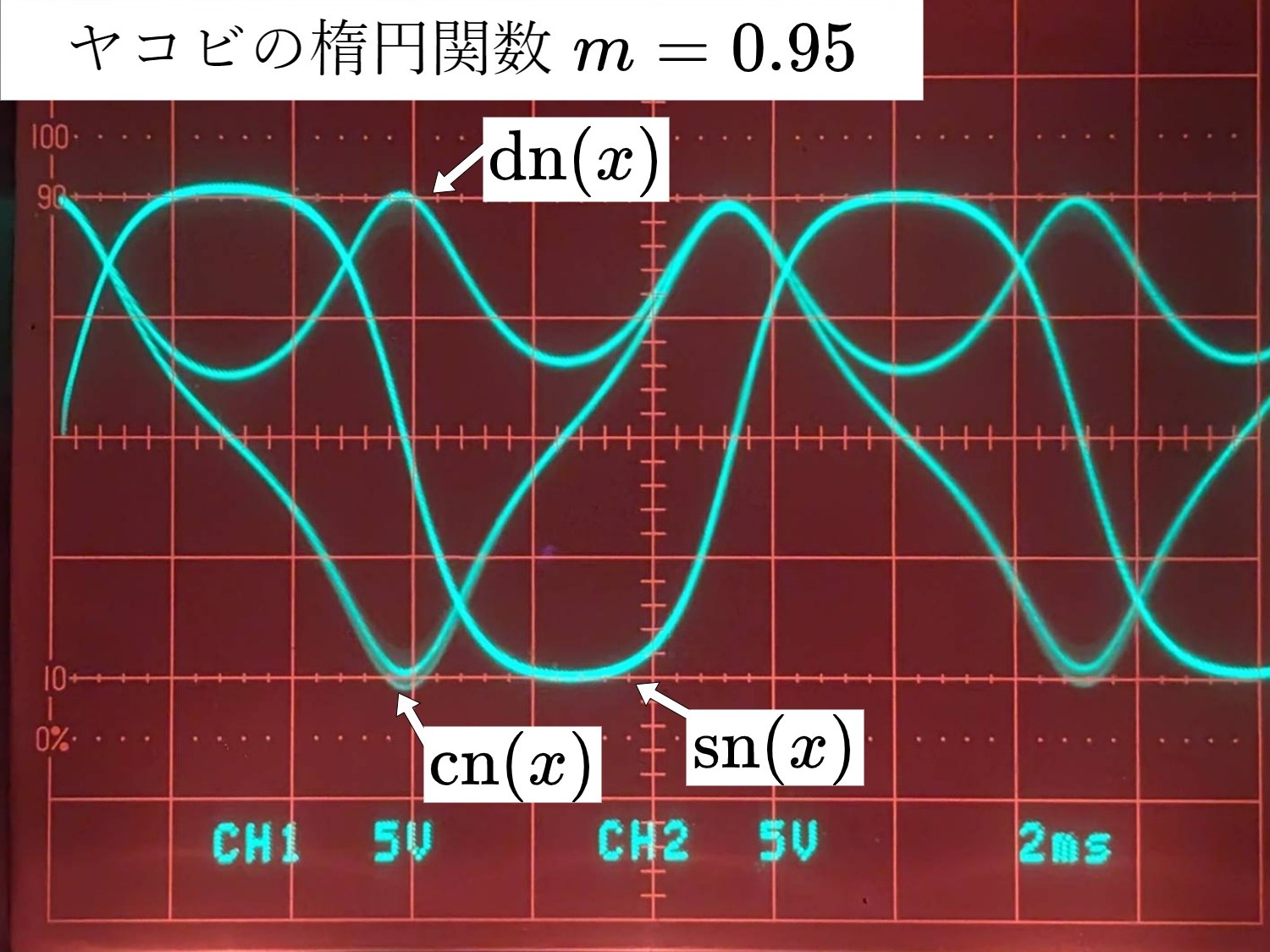
楕円積分とヤコビの楕円関数連立非線形微分方程式から楕円関数を生成する |
|
|
ローレンツ方程式の変種Edward N. Lorenz. "Irregularity: a fundamental property of the atmosphere" (1984) にあるカオスアトラクタ |
|
|
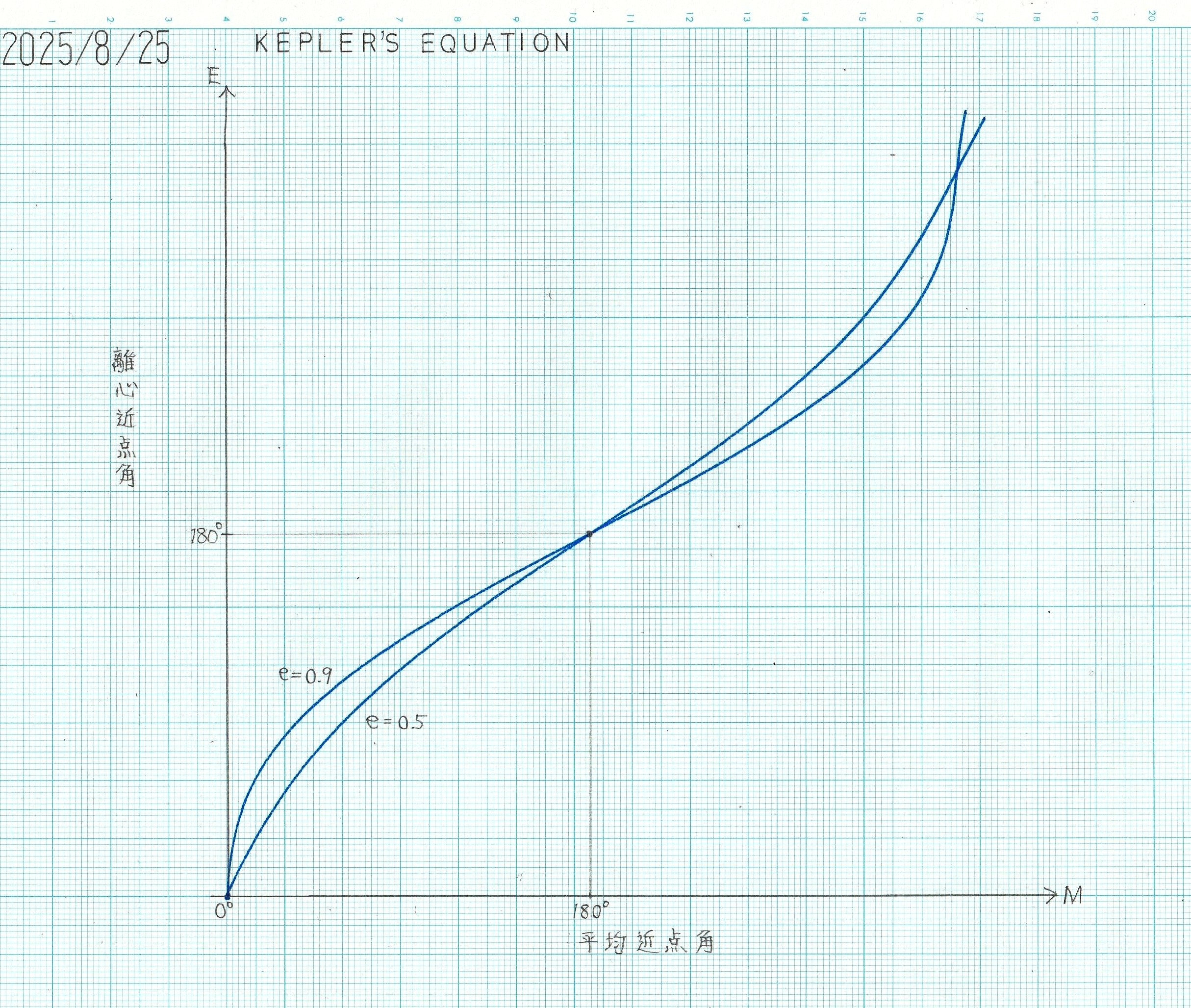
ケプラー方程式解析的に解けない非線形方程式として有名なケプラー方程式を工夫して解く |
|
|
ラザフォード散乱のシミュレーションガイガー=マースデンの実験で確かめられた、アルファ粒子の金原子核による後方散乱のシミュレーション |
|
|
Halvorsen アトラクタ式の形に対称性がある1階3元常微分方程式で表されるカオスアトラクタ |
|
|
Aizawa アトラクタ(Langford アトラクタ)謎の多いカオスアトラクタ |
|
|
multi-wing ローレンツアトラクタの変種ローレンツアアトラクタに修正を加え翼の数が増えたアトラクタを2種シミュレーションする。 [Zenghui Wang et al 2009.]/[Simin Yu et al 2008.] |
|
|
最適経済負荷配分出力の計算数理計画法の問題をアナログコンピュータで扱う |
|
|
(準備中)
|