複素関数と等位線・高次多項式の複素根
目次
1.複素関数の絶対値(の2乗)の等位線と最急降下曲線
複素数変数のn次多項式関数
\[\sum_{k=0}^{n}{a_{k}z^{k}}\qquad(\,z\in\mathbb{C}^{1},\,n\in{\mathbb{N},\,a_{n}\in{\mathbb{R}}}\,)\tag{1}\]
の根を求めたいときや、複素関数としての性質を調べたいとき、その絶対値 \(|f(z)|\) もしくはその2乗 を \(z\) 平面上にプロットすることは有意義なことである。その場合は、複素数から実数へ写す関数となるわけだから、2実変数関数と同様の扱いが可能になる。
今回は、複素変数高次多項式の絶対値(の2乗)の等位線 (Level Line, Contour Line) 及びそれに直交する曲線(最急降下曲線)をアナログコンピュータで描出することを目標とする。
2.1 複素関数
複素数 \(z=x+i\,y\;(x,y\in\mathbb{R}^{1})\) についての関数 \(w\) は正則であり、
\[w(z)\equiv{u(x,y)+i\,v(x,y)\quad(u,v\in{\mathbb{C}^{1}})}\tag{2}\]
このとき、その絶対値の2乗を新たに関数 \(f\,:\,\mathbb{C}\to\mathbb{R}_{\geq{0}}\) として定める。
\[|w(z)|^2={w(z)\,\overline{w(z)}}=u^2+v^2\equiv{f(x,y)}\tag{3}\]
2.2 等位線
実数値関数\(g\,{:}\mathbb{C}^{1}\to\mathbb{R}^{1}\) \(z\) を平面上にプロットしたときの等位線(等値集合)\(L_{C}\)は、任意定数 \(C\,(\geq{0})\) を用いて
\[L_{C}\equiv\{(x,y)\in\mathbb{R}^{2}|g(x,y)=C\}\tag{4}\]
として定義される。
2.3 勾配ベクトル
実数値関数\(g\,{:}\mathbb{C}^{1}\to\mathbb{R}^{1}\) \(z\) は実部・虚部が連続で1階微分可能とする。\(g(z)\neq{0}\) を満たす全てのz平面上の点で勾配
\[\nabla{g}\equiv\,\biggl(\frac{\partial{g}}{\partial{x}},\frac{\partial{g}}{\partial{y}}\biggr)\in\mathbb{R}^{2}\tag{5}\]
を定義できる。ここで、形式的に複素勾配ベクトル
\[\nabla{g}_{\mathbb{C}}\equiv\,\biggl(\frac{\partial{g}}{\partial{x}}+i\frac{\partial{g}}{\partial{y}}\biggr)\in\mathbb{C}^{1}\tag{6}\]
を導入し、ウィルティンガー微分
\[\frac{\partial}{\partial{z}}=\frac{1}{2}\left(\frac{\partial}{\partial{x}}-i\frac{\partial}{\partial{y}}\right)\quad\frac{\partial}{\partial{\overline{z}}}=\frac{1}{2}\left(\frac{\partial}{\partial{x}}+i\frac{\partial}{\partial{y}}\right)\tag{7}\]
を \(g\) について用いると
\begin{eqnarray}\frac{\partial{g}}{\partial{\overline{z}}}&=&\frac{1}{2}\left(\frac{\partial{f}}{\partial{x}}+i\frac{\partial{g}}{\partial{y}}\right)\\\\\therefore\;2\frac{\partial{f}}{\partial{\overline{z}}}&=&\left(\frac{\partial{f}}{\partial{x}}+i\frac{\partial{f}}{\partial{y}}\right)\tag{8}\end{eqnarray}
なので、(6),(8)より、\(f\) の複素勾配ベクトルは
\[\nabla{g}_{\mathbb{C}}=2\frac{\partial{g}}{\partial{\overline{z}}}=\frac{\partial}{\partial{\overline{z}}}\left\{w(z)\overline{w(z)}\right\}\tag{9}\]
と表される。
\(w(z)\) は正則であるから、たとえばその絶対値の2乗 \(f\) は連続かつ \(\mathbb{R}^2\) 上で1階微分可能であり、
2.4 最急降下曲線
実数値関数 \(g\,{:}\mathbb{C}^{1}\to\mathbb{R}^{1}\) (実部・虚部は連続で1階微分可能)に対して、ある区間 \(I\subset\mathbb{R}\) 上の連続で微分可能な曲線 \(\gamma(t):I\to\mathbb{C}^{1}\) がすべての \(t\subset{I}\)に対して
\[\frac{\mathrm{d}\gamma}{\mathrm{d}t}=-\nabla_{\mathbb{C}}{g(\gamma(t))}\tag{10}\]
を満たすとき、\(\gamma\)を \(g\)に関する最急降下曲線と定義する。
その曲線は初期条件として任意の \(z_0\) が与えられれば一意に定まる。\(\gamma\) は、初期値から出発して、常に\(g(z)\) の勾配ベクトルの逆方向に動く点の軌跡である。関数 \(g\) の値が最も早く減少する方向に接ベクトルを持つ曲線ともいえる。
また、等位線と最急降下曲線は互いに直交する。(証明は簡単であるが省略)
2.5 最急降下曲線及び等位線が満たす微分方程式
今までの議論では複素関数 \(w(z)\) は単に正則であるという条件であったが、より厳しい条件を課し、実数係数の\(n\)次多項式関数であるとする。
\[w(z)\equiv\sum_{k=0}^{n}{a_{k}z^{k}}\qquad(\,n\in{\mathbb{N},\,a_{n}\in{\mathbb{R}}}\,)\tag{11}\]
その場合、 \(f=|w(z)|^2\) も実数係数の多項式関数となるので勾配が定義可能である。\(f(z)=u^2(x,y)+i\,v^2(x,y)\) の複素勾配ベクトルは
\begin{eqnarray}\nabla_{C}{f(z)}&=&\frac{\partial}{\partial{\overline{z}}}\left\{w(z)\overline{w(z)}\right\}\\\\ &=&\,\frac{\partial}{\partial{\overline{z}}}\left\{w(z)w(\overline{z})\right\}\\\\ &=&\,w(z)\,\frac{\partial{w(\overline{z})}}{\partial{\overline{z}}}\\\\ &=&\,w(z)\,\overline{\frac{\partial{w(z)}}{\partial{z}}}\tag{12}\end{eqnarray}
ゆえに、最急降下曲線が満たす微分方程式は、
\begin{eqnarray}\frac{\mathrm{d}z}{\mathrm{d}t}&=&-\nabla_{\mathbb{C}}f\\\\&=&-\,w(z)\,\overline{\frac{\partial{w(z)}}{\partial{z}}}\tag{13}\end{eqnarray}
となる。等位線は最急降下曲線と直交するということなので、式(13)の右辺に \(i\) もしくは \(-i\) を掛けると等位線が満たす微分方程式が求まる。
\[\frac{\mathrm{d}z}{\mathrm{d}t}=\pm\,{i}\,w(z)\,\overline{\frac{\partial{w(z)}}{\partial{z}}}\tag{14}\]
※ 複素多項式関数 \(w(z)\) の等位線及び最急降下曲線の定義には、\(g\) として絶対値の2乗の関数 \(f=w(z)\overline{w(z)}\)を用いることが多いが、絶対値そのもの \(|w(z)|\) を使う手法もある。後者は演算器の数を節約できるが、前者の描く等位線や最急降下曲線と必ずしも一致するとはかぎらない。しかし、\(w(z)\) の根の探索と表示のうえで困ることは無いので、どちらを使っても構わない。
2.6 等位線の演算方程式
等位線の式(15)の右辺の係数として正を選び、実部と虚部に分離すると、
\begin{eqnarray}\frac{\mathrm{d}z}{\mathrm{d}t}&=&{i}\,\biggl\{\mathrm{Re}\bigl(w\bigr)+i\,\mathrm{Im}\bigl(w\bigr)\biggr\}\,\biggl\{\mathrm{Re}\Bigl(\frac{\mathrm{d}z}{\mathrm{d}t}\Bigr)- i\,\mathrm{Im}\Bigl(\frac{\mathrm{d}z}{\mathrm{d}t}\Bigr)\biggr\}\\\\ &=&{i}\,\Biggl[\mathrm{Re}\bigl(w\bigr)\mathrm{Re}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)+ \mathrm{Im}\bigl(w\bigr)\mathrm{Im}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)+ i\,\biggl\{-\mathrm{Re}\bigl(w\bigr)\mathrm{Im}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr) +\mathrm{Im}\bigl(w\bigr)\mathrm{Re}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)\biggl\}\Biggr]\\\\ &=&\mathrm{Re}\bigl(w\bigr)\mathrm{Im}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)- \mathrm{Im}\bigl(w\bigr)\mathrm{Re}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)+ i\,\biggl\{\mathrm{Re}\bigl(w\bigr)\mathrm{Re}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)+ \mathrm{Im}\bigl(w\bigr)\mathrm{Im}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)\biggl\}\tag{15}\end{eqnarray}
以上のことから、\(\mathrm{Re}\Bigl(\frac{\mathrm{d}z}{\mathrm{d}t}\Bigr)\) を入力とし、\(\mathrm{Re}\bigl(w\bigr)\) を出力とする積分器と、\(\mathrm{Im}\Bigl(\frac{\mathrm{d}z}{\mathrm{d}t}\Bigr)\) を入力とし、\(\mathrm{Im}\bigl(w\bigr)\)を出力とする積分器の2つを用意し、(16)式を用いて帰還ループを閉じてあげれば、演算回路が完成することとなる。すなわち等位線のほうの原方程式は
\begin{cases}\displaystyle\mathrm{Re}\biggl(\frac{\mathrm{d}z}{\mathrm{d}t}\biggr)=\mathrm{Re}\bigl(w\bigr)\mathrm{Im}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)- \mathrm{Im}\bigl(w\bigr)\mathrm{Re}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)\\\\\displaystyle\mathrm{Im}\biggl(\frac{\mathrm{d}w}{\mathrm{d}z}\biggr)=\mathrm{Re}\bigl(w\bigr)\mathrm{Re}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)+ \mathrm{Im}\bigl(w\bigr)\mathrm{Im}\Bigl(\frac{\mathrm{d}w}{\mathrm{d}z}\Bigr)\tag{16}\end{cases}
最急降下曲線のほうも同様の計算で導くことができるが、ここでは省略する。
いずれの場合も、\(\mathrm{Re}\bigl(w\bigr)\)、\(\mathrm{Im}\bigl(w\bigr)\) などの演算信号は \(z\in\mathbb{C}^{1}\) についての多項式であるから、\(z\) のべき乗 \(z,\,z^2,\,z^3\,...\) を実部と虚部のペアで生成する必要がある。
複素数の2乗については、乗算器が加算器に比べ豊富にある場合は
\begin{cases}\mathrm{Re}\bigl(z^2\bigr)=\mathrm{Re}\bigl(z\bigr)^2-\mathrm{Im}\bigl(z\bigr)^2\\\\\mathrm{Re}\bigl(z^2\bigr)=2\mathrm{Re}\bigl(z\bigr)\,\mathrm{Im}\bigl(z\bigr)\tag{17}\end{cases}
の関係を直接実装すればいいが、乗算器より加算器が多い場合は、実部の方を因数分解して乗算器を1つ減らすほうがよいだろう。(そのかわり加算器の数は増える。)
当然ながら、式の形によってはスケーリングを施す必要が出てくる。特に加算器の出力には注意すべきである。飽和しやすい信号は、微分値 \({\mathrm{d}w}/{\mathrm{d}z}\) の実部・虚部であり、優先的にスケールダウンすること。その後段にある乗算器や加算器もそれに伴いスケーリング係数が掛けられることになるが、最後に積分器 \(\mathrm{d}z/\mathrm{d}t\) に入力する際に辻褄を併せればよい。(その積分器入力ゲインが等高線描画の速度を決定する。)
また、等高線を描画する範囲が\(z\)のマシンユニット範囲ギリギリにまで及ぶ場合、\(z^2\), \(z^3\)も飽和する恐れがある。その際も同様にスケールダウンし、後段で辻褄合わせをおこなうこと。
2.7 等位線の値を陽に定めるとき
(16)の式を演算回路に直せば等位線は描かれるが、描きたい等位線の値 \(w(z)\overline{w(z)}=C\) を直接指定することができない(Cの値を直接与えるのではなく、絶対値の2乗がCとなるz平面上の座標点を積分器の初期条件として与える必要がある)ので、与える初期条件が少しでもずれると描かれた等位線も。さらに、何らかの理由で積分器の誤差が大きくなると、等位線の描くループが複素平面上で1周しても閉じないこともありえる。
それらを解決するために、常に\(G(z)=w(z)\overline{w(z)}-C\) の値が0に等しくなるよう演算回路全体のゲインを補正する項を導入する方法が考案されている。[1]
\(K\) を正のゲインとして、微分方程式は以下のようになる。
\[\frac{\mathrm{d}z}{\mathrm{d}t}=\bigl\{\pm\,{i}-2KG(z)\bigr\}\,w(z)\,\overline{\frac{\partial{w(z)}}{\partial{z}}}\tag{18}\]
(14)式のかわりにこの式を演算方程式とすれば、多少初期位置がずれたとしても、軌道はゲイン \(K\) の時定数で\(C\)の等位線に「吸着」し、定常誤差も小さくできる。ただし、必要となる演算器の数が多くなることが難点である。ゲイン\(K\)が大きいほど正しい軌道への収束も早くなるが、あまりにも大きすぎると回路が不安定になる。
2.8 演算結果
以下の4次関数
\[w(z)=0.25z^4-0.06z^3+0.05z^2+0.1z-0.1\tag{19}\]
\[\frac{\mathrm{d}w(z)}{\mathrm{d}z}=z^3-0.18z^2+0.1z+0.1\tag{20}\]
を(16)式に則って演算し、等位線を描いた結果は以下のようになった。
図1 (19)式の \(w(z)\overline{w(z)}\) の等位線(左:厳密解 右:アナログ計算機解)
\(C\) の値を直接定めることができないため初期位置を精度よく与えることに労力を注ぐ必要がなり、誤差も生じやすいが、それでも厳密解によく一致している。工夫できる点として、等位線が半周したら、積分器に入力する信号の符号を変えてもう半周を描画する方法を採れば、累積誤差が小さくなり、ある程度精度のよい結果が得られる。
同様の方法で最急降下曲線を演算した結果を図2に示す。
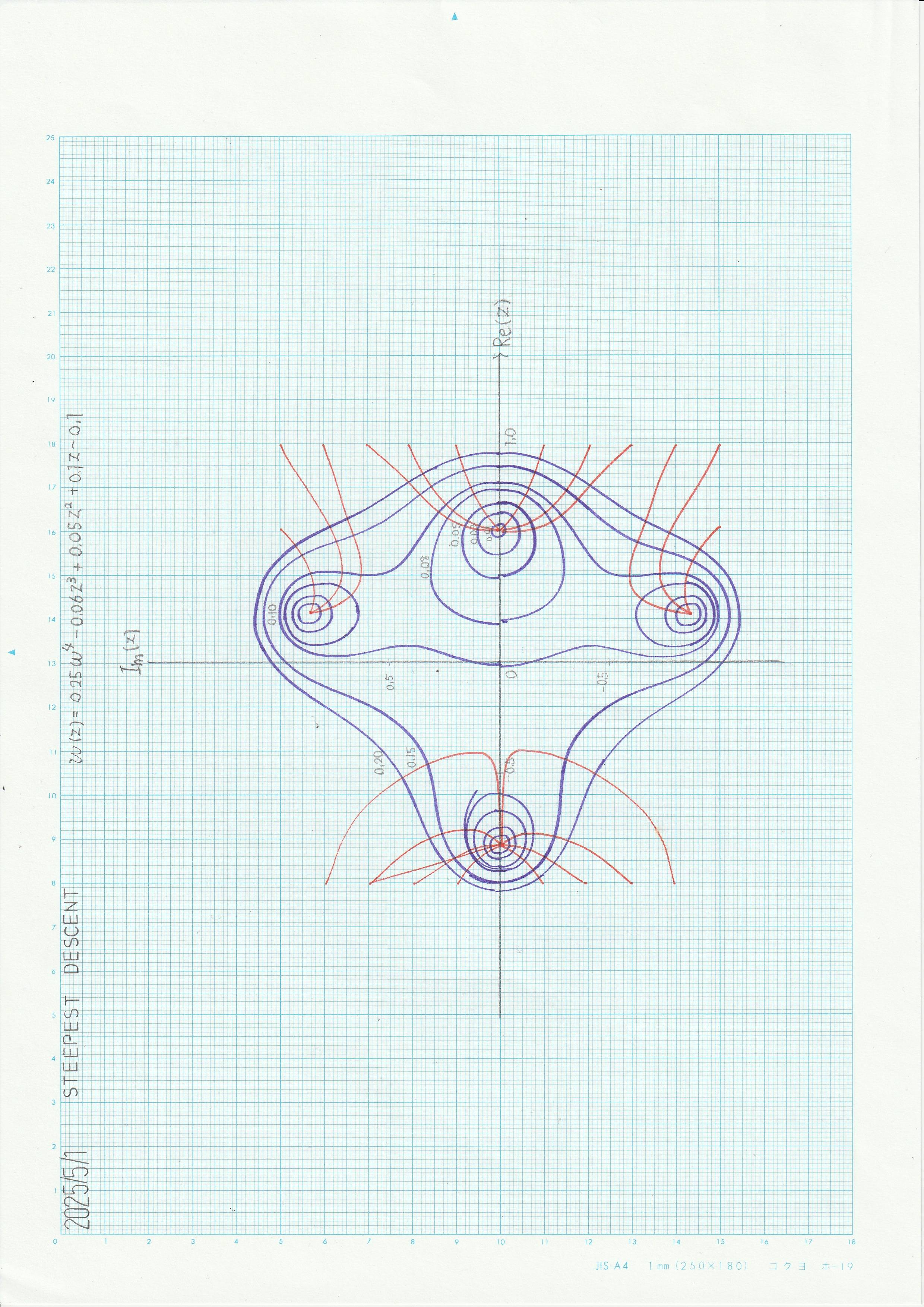
図2 (19)式の等位線と最急降下曲線
つぎに、\(C\) の値を陽に与え、誤差を補正する方法(式(18))を用いて次の3次関数
\[w(z)=z^3+0.5z^2+0.5z-0.5\tag{21}\]
\[\frac{\mathrm{d}w(z)}{\mathrm{d}z}=3z^2+z+0.5\tag{22}\]
の等位線を描いた結果と、その演算回路を示す。

図3 (19)式の \(w(z)\overline{w(z)}\) の等位線(左:厳密解 右:アナログ計算機解)
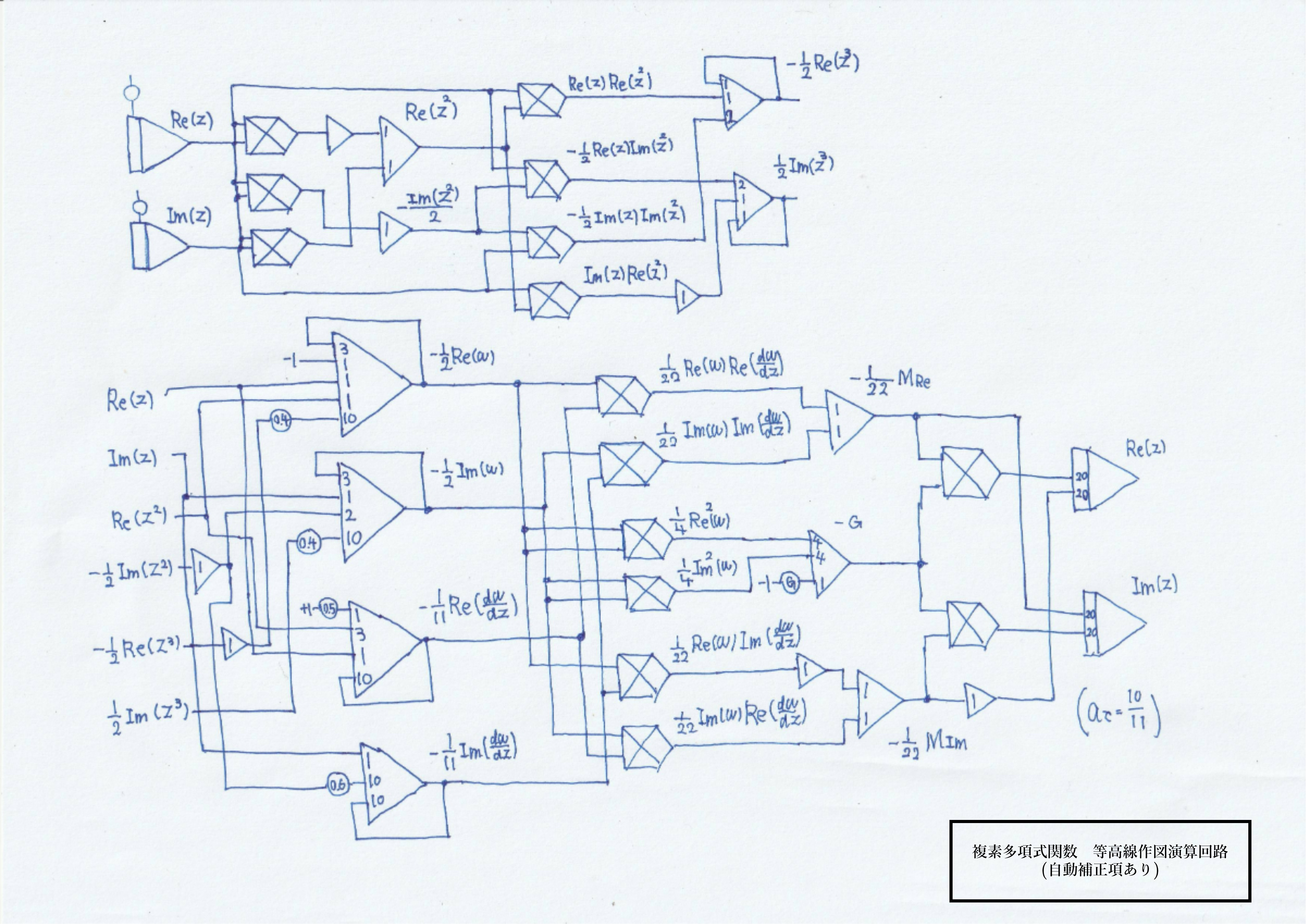
図4 図3の演算回路
図6から、後者の手法の方が精度が極めて良いことがわかる。なにより、初期値とその点の絶対値をいちいち計算しなくて良いことがありがたい。
参考までに、文献[1] (1965年) に掲載されている、当時の低速型アナログ計算機(乗算器はサーボ式乗算器である)を用いた6次関数のプロットを引用しておく。
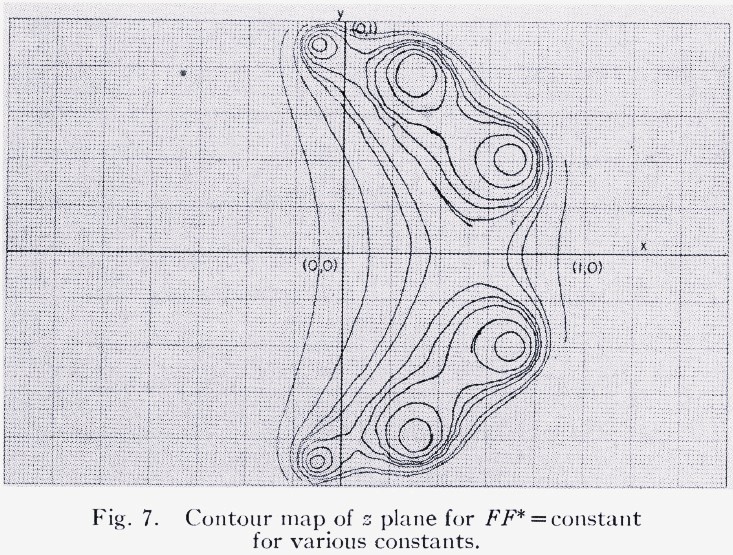
図5 文献[1] Fig.7より 6次関数の等高線の演算結果
軌道が歪んでいるのは、当時の演算増幅器のゲイン不足・オフセット誤差が効いていることが原因と思われる。
※注意事項※
(1) 上記のように等位線描画回路は複雑であるから、結線間違いを犯しやすいので十分注意する。正しい演算を行うと、根付近の軌道は実関数系 y(x) で考えた時の中心点(渦点)になるはずであるが、根に湧き出しや吸い込みが発生したならば、十中八九、回路中で実部と虚部のゲイン差が生じて減衰・発散項が現れていると考えてよい。その場合、丁寧に各演算器の入力ゲインを見直すと間違いが見つかるだろう。軌道上で明らかに不自然な不連続点が生じた場合、演算回路のどこかで飽和が発生している可能性が高い。また、根に近い部分では絶対値が極めて小さく(SN比が悪く)なり、軌道に歪が生じることもある。スケーリング係数は臨機応変に変更することが賢明であろう。
(2) 今回のように最急降下曲線や等位線を描画するほかに、等位線描画回路に減衰項をあえて付与し、初期点から等位面に沿って根へ落ちていく軌道を描画する求根手法も存在する。
(3) 最急降下曲線の演算回路として、通常のデカルト座標系(Cartesian coordinate system)を用いた手法を説明したが、極座標系(polar coordinate system)を採用したものも考案されている。後者については文献[5]のp276~p277などに詳しい。
2.アイソグラフ
高次多項式の複素根を求める方法として、アイソグラフと呼ばれる手法もある。
関数\(w(z)\,(z\in{\mathbb{C}})\) が実数係数の多項式関数であるとする。
\[w(z)=\sum_{k=0}^{n}{a_{k}z^{k}}\qquad(\,n\in{\mathbb{N},\,a_{n}\in{\mathbb{N}}}\,)\tag{23}\]
変数 \(z\) を
\[z=r\,e^{i\theta}\quad{(\,r\gt{0)}\,}\tag{24}\]
と極座標表示すると、
\begin{eqnarray}w(z)&=&\sum_{k=0}^{n}{a_{k}\,r^{k}e^{i\,k\theta}}\\\\&=&\sum_{k=0}^{n}{a_{k}\,r^{k}\left\{\cos{(k\theta)}+i\,\sin{(k\theta)}\right\}}\\\\&=&\sum_{k=0}^{n}{a_{k}\,r^{k}\cos{(k\theta)}}+i\sum_{k=0}^{n}{a_{k}\,r^{k}\sin{(k\theta)}}\tag{25}\end{eqnarray}
ここで、絶対値\(r\) を係数器で設定する定数とし、偏角 \(\theta\) を演算独立変数とみなせば、関数 \(w\) の実部と虚部
\[\mathrm{Re}(w)=\sum_{k=0}^{n}{a_{k}\,r^{k}\cos{(k\theta)}}\,,\quad\mathrm{Im}(w){\sum_{k=0}^{n}{a_{k}\,r^{k}\cos{(k\theta)}}}\tag{26}\]
を演算することは容易である。(sinやcosは2階微分方程式を解くサークルテスト回路で生成できる。)
上記2信号をXYモードのオシロスコープやXYレコーダに入力して描く軌跡を観察し、 \(0\lt\theta\lt2\pi\) の範囲で原点を通過するのなら、その点の写像元の \(z\) が多項式関数 \(w\) の根であることが分かる。よって、その点の偏角 \(\theta\) を、計時もしくは別個で \(\mathrm{Re}(w)-t\) グラフ、\(\mathrm{Im}(w)-t\)グラフを得ることで調べ、既知の \(r\) とあわせて複素根を求めることができるというものである。
1節と同じ4次方程式について、写像先の軌跡と時系列グラフを求めた結果を次に示す。
図6 アイソグラフ
3.参考文献
[1] A. Hausner. "Analog Computer Techniques for Problems in Complex Variables," in IEEE Transactions on Electronic Computers, vol. EC-14, no. 6, pp. 898-908, 1965.
[2] Byron O. Marshall, "The Electronic Isograph for Roots of Polynomials," J. Appl. Phys. 1 April 1950; 21 (4): 307–312. https://doi.org/10.1063/1.1699660
[3] A. Hausner. “Machines for Solving Algebraic Equations.” Mathematical Tables and Other Aids to Computation, vol. 1, no. 9, 1945, pp. 337–53. https://www.jstor.org/stable/2002339
[4] 佐々木 彬夫, 小沢 保知.「ハイブリッド・アイソグラフ」情報処理学会 ,13巻, 2号 ,1972. https://ipsj.ixsq.nii.ac.jp/records/8249
[5] 山下 英夫. 「電子計算機 アナログ計算機編」第2版, オーム社, 1959.