楕円積分とヤコビの楕円関数
目次
1.導出
1.1 第1種不完全楕円積分
楕円の周長を求める際に出現する積分が第2種不完全楕円積分であり、被積分関数についてその逆数をとった積分が第1種不完全楕円積分である。積分範囲が\([0.2\pi]\)のとき完全楕円積分という。
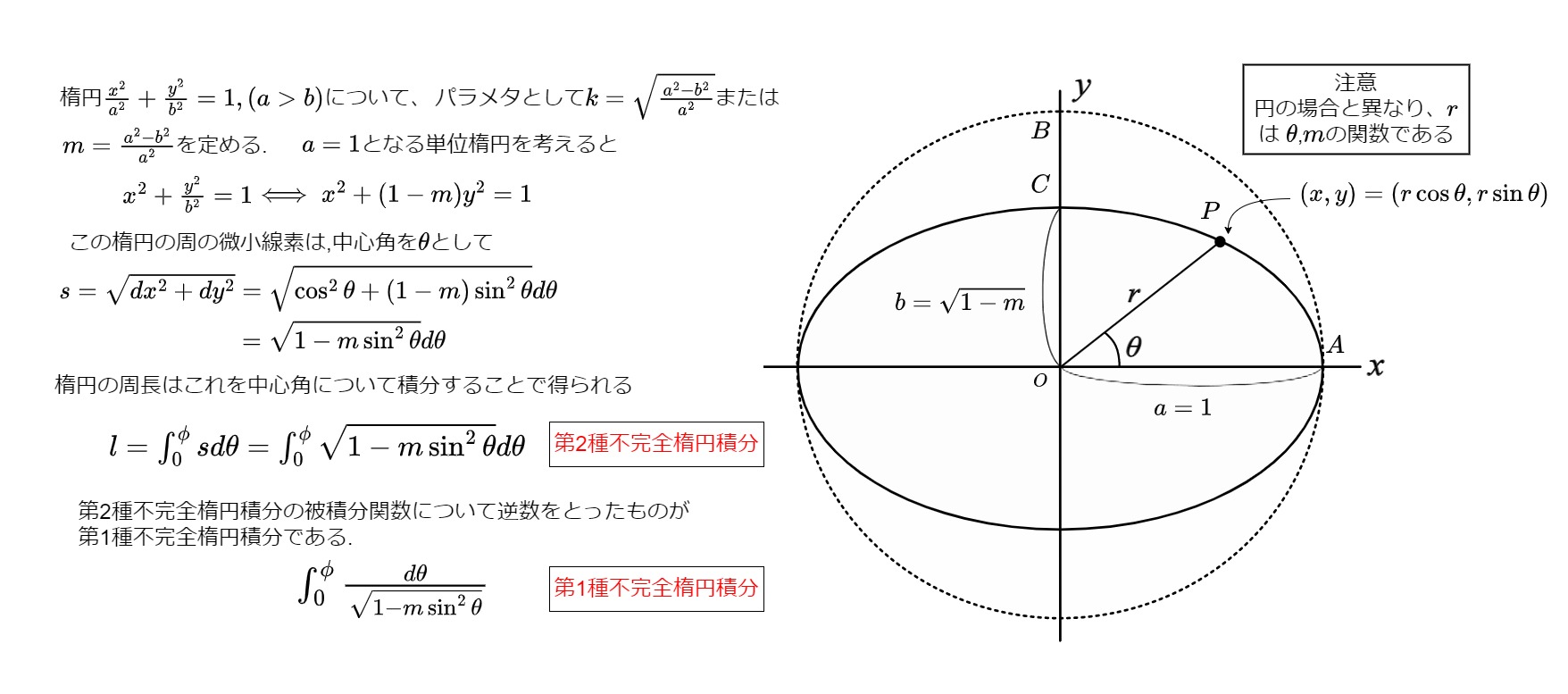
図 1
1.2 ヤコビの楕円関数
ヤコビの楕円関数は第1種不完全楕円積分の逆関数として定義できる。母数(の2乗)を\(0\leq m\leq 1\)として
\[u=\int_0^{\phi}{\frac{\mathrm{d}\theta}{\sqrt{1-m\sin{\theta}}}}\tag{1}\]
とおくと、
\[\mathrm{sn}\;{u}=\sin{\phi}\tag{2}\]
\[\mathrm{cn}\;{u}=\cos{\phi}\tag{3}\]
\[\mathrm{dn}\;{u}=\sqrt{1-m\sin^2{\phi}}\tag{4}\]
\(\mathrm{sn}\)は奇関数、\(\mathrm{cn}\)、\(\mathrm{dn}\)は偶関数である。
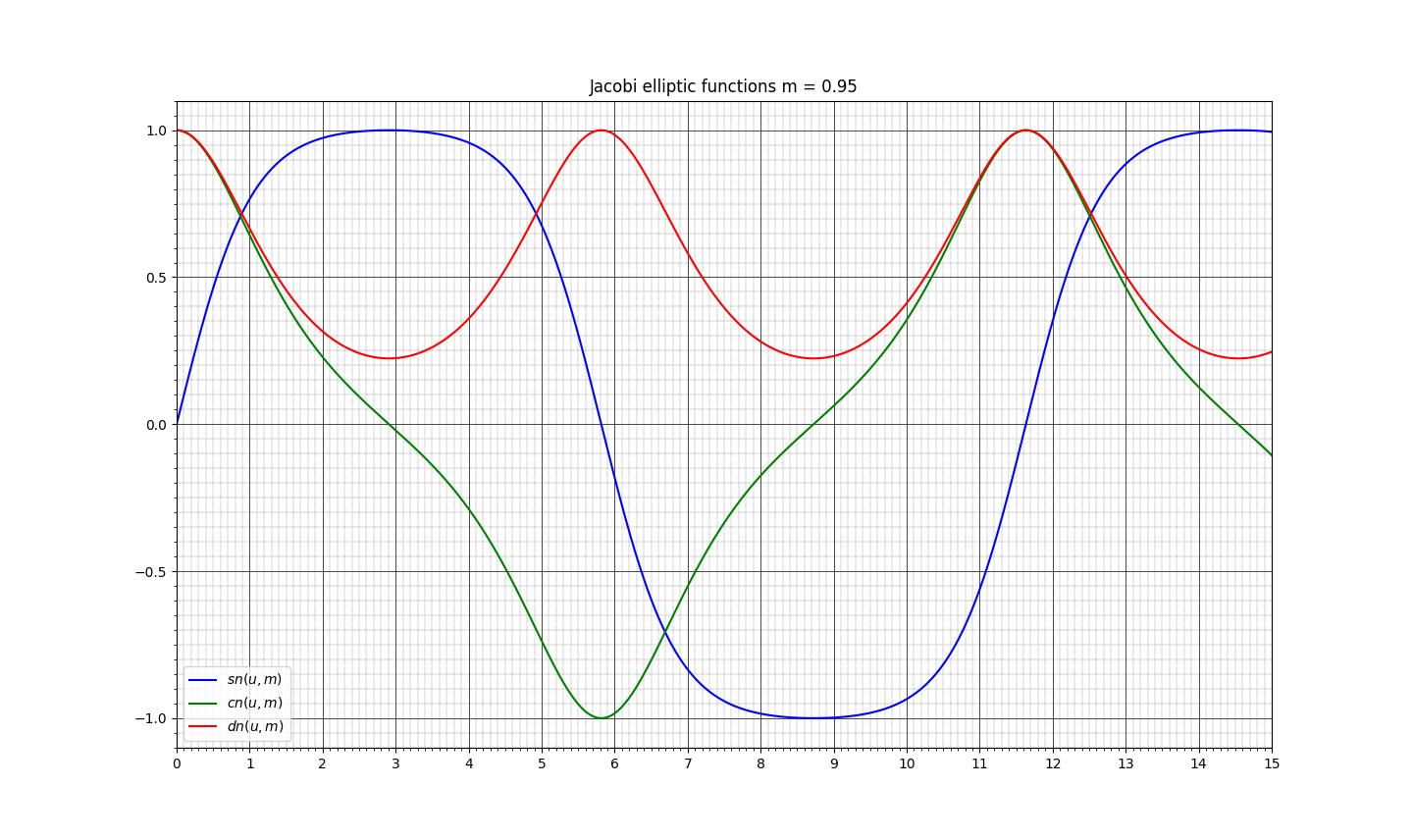
図2 実変数の場合のヤコビの楕円関数のグラフ
また、
\[\mathrm{cn}\;{u}=\sqrt{1-\mathrm{sn}^2\;{u}}\tag{5}\]
\[\mathrm{sn}^2\;{u}+\mathrm{cn}^2\;{u}=1\tag{6}\]
\[m\mathrm{sn}^2\;{u}+\mathrm{dn}^2\;{u}=1\tag{7}\]
なる関係が成り立つ。sn、cn、dnの導関数は以下のような3元連立の非線形微分方程式を構成する。
\begin{cases}
\displaystyle\frac{\mathrm{d}}{dz} \operatorname{sn}(z) = \operatorname{cn}(z, m) \operatorname{dn}(z, m), \\\\\displaystyle\frac{\mathrm{d}}{\mathrm{d}z} \operatorname{cn}(z) = -\operatorname{sn}(z, m) \operatorname{dn}(z, m), \\\\
\displaystyle\frac{\mathrm{d}}{\mathrm{d}z} \operatorname{dn}(z) = -m \;\operatorname{sn}(z, m) \operatorname{cn}(z, m).\tag{8}
\end{cases}
上式に基づきアナログコンピュータでsn、cn、dnを生成することは容易である。また、定義から値域の絶対値が1を超えないことは明らかであるので、電圧換算は不要である。
2.アナログコンピュータプログラム
(8)式をもとに演算回路をつくる。
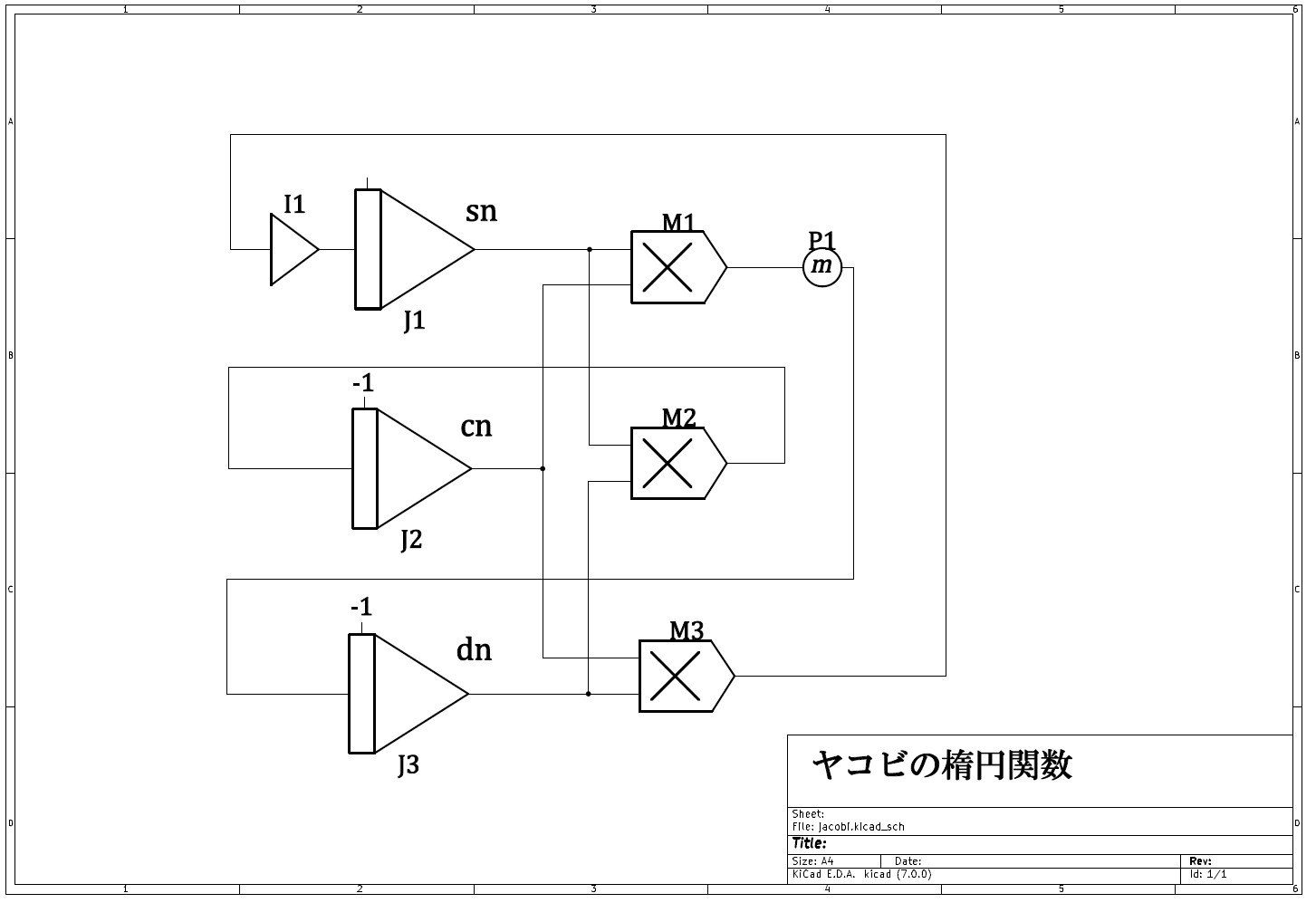
図3 ブロックダイヤグラム
3.結果
\(m=0.95\)の場合の、高速繰り返しモードおよび低速モードにおける演算結果を示す。
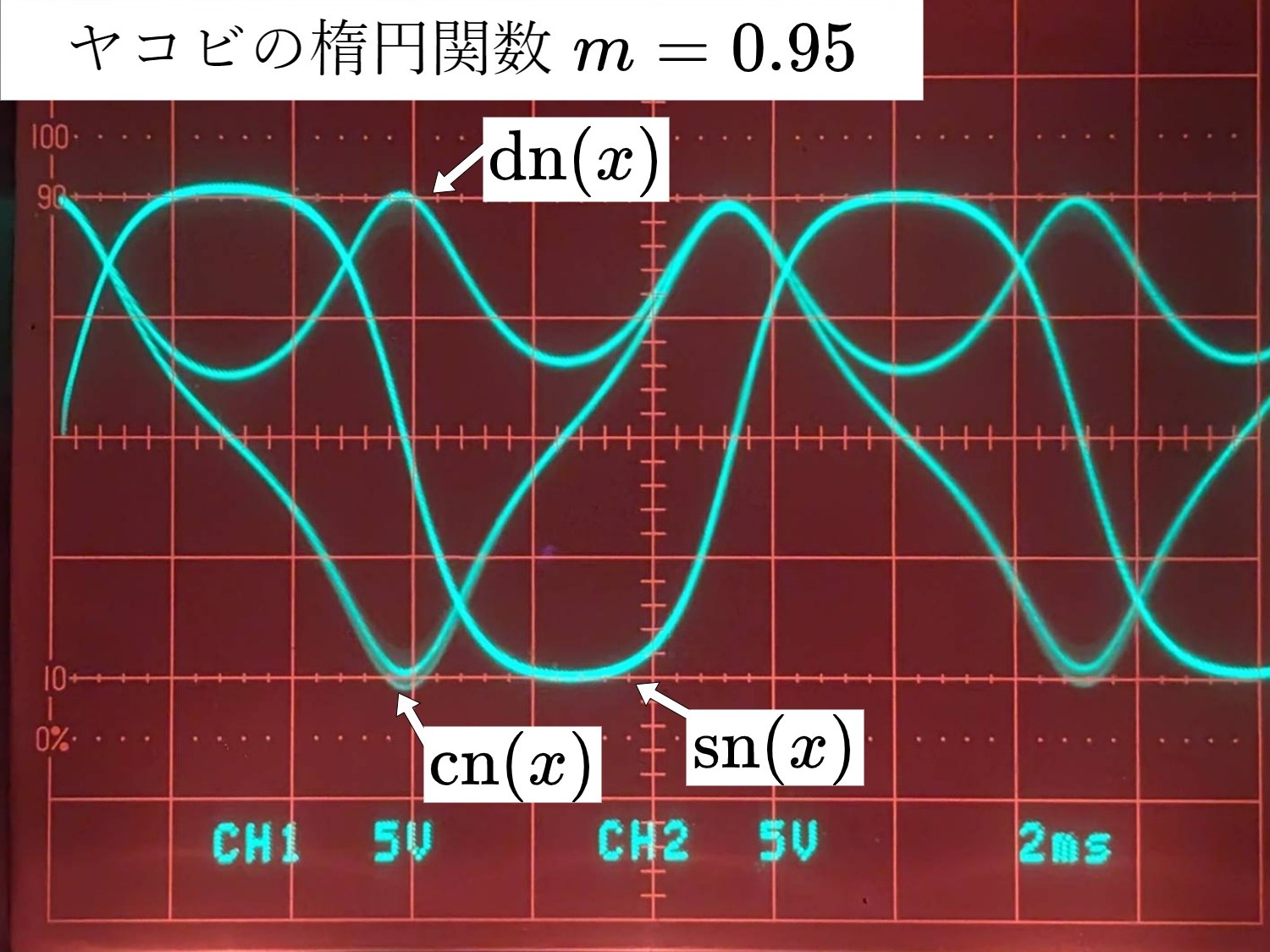
図4 高速繰り返しモードにおける演算結果
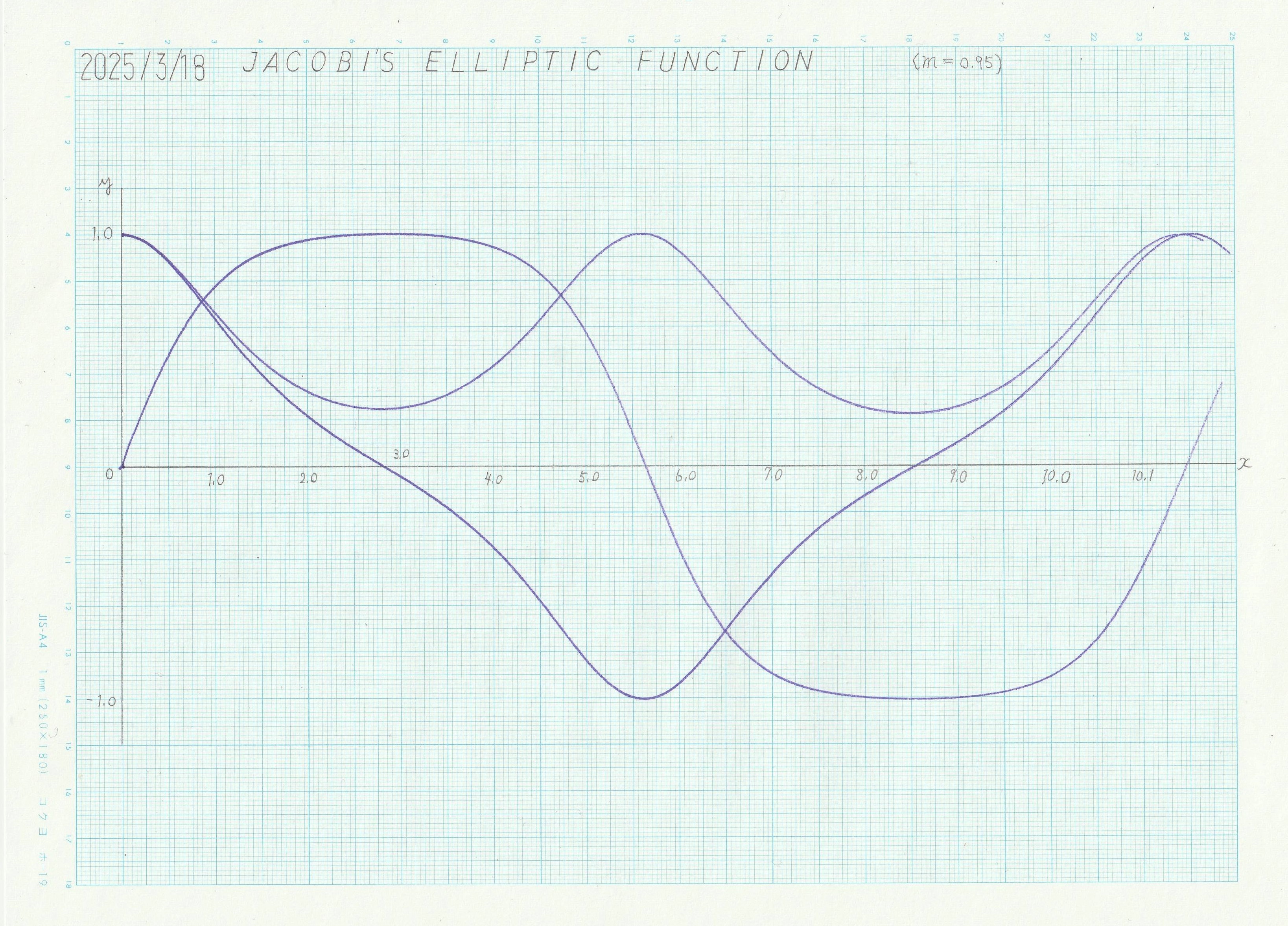
図5 低速モードにおける演算結果
これらは図2のグラフに極めてよく一致している。
次に、高速繰り返しモードで母数 \(m\) を複数の異なる値で演算して同時に表示させた。演算信号周波数は数十kHz程度である。
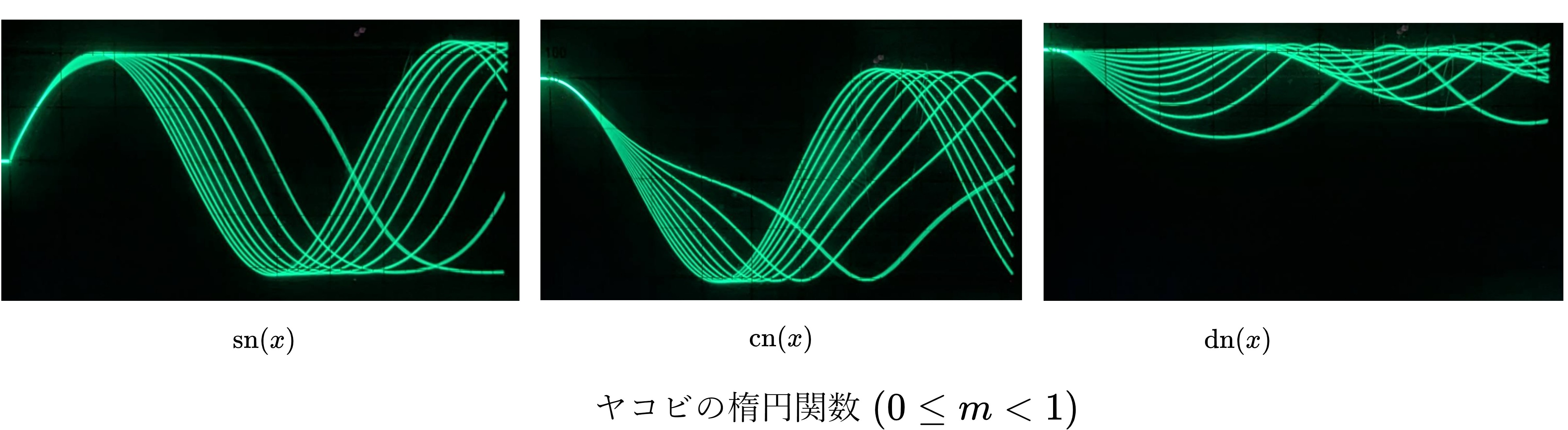
図6
\(m\)の間隔はおよそ0.1である。\(m\)の値が大きくなるにつれ、周期は激しく増大する。\(\mathrm{sn}(x)\)は、\(m\rightarrow{0}\)で\(\sin(x)\)に、\(m\rightarrow{1}\)で\(\tanh(x)\)に漸近する。\(m\rightarrow{0}\)のとき\(\mathrm{cn}(x)\)は\(\cos(x)\)へ、\(\mathrm{dn}(x)\)は、\(y=1\)に近づくが、いずれも\(m\rightarrow{1}\)で\(\mathrm{sech(x)=1/\cosh(x)}\)に漸近する。
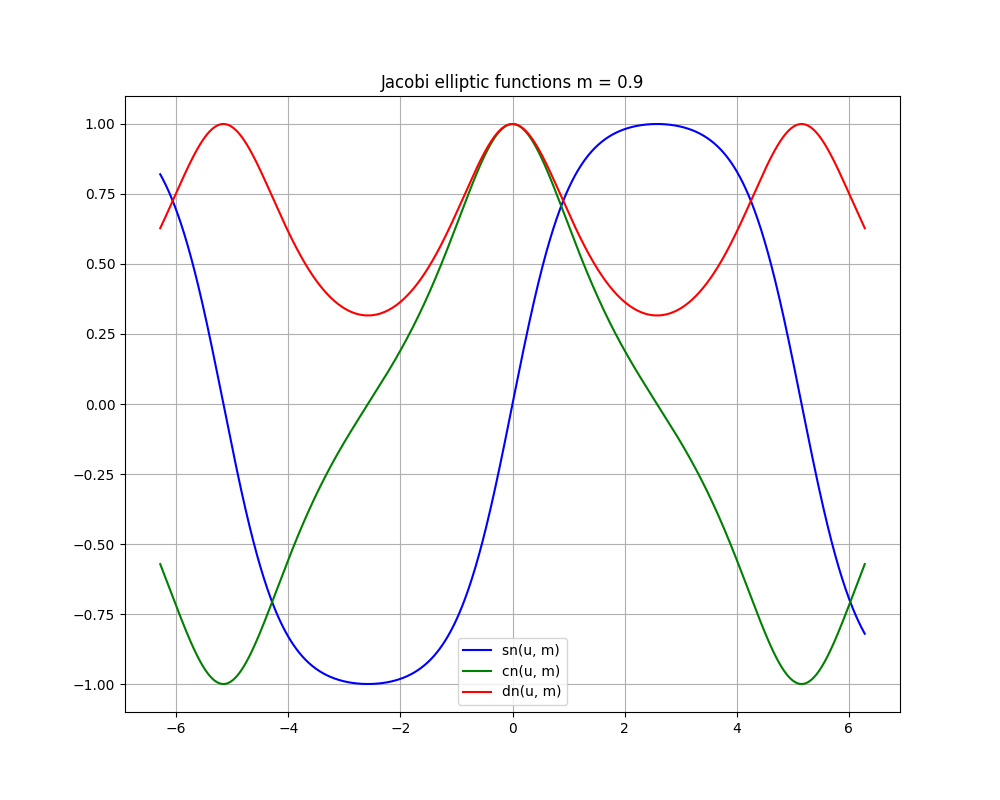
参考までに、scipyの特殊関数モジュールで計算した、異なる母数でのヤコビの楕円関数のグラフを次に示す。
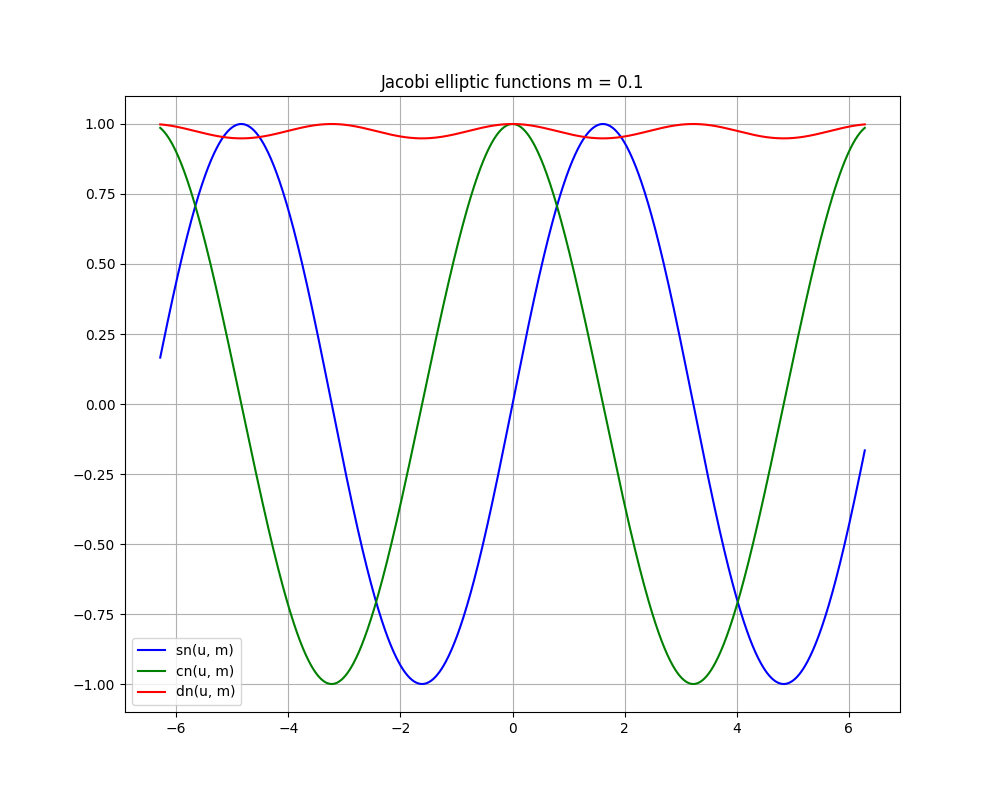
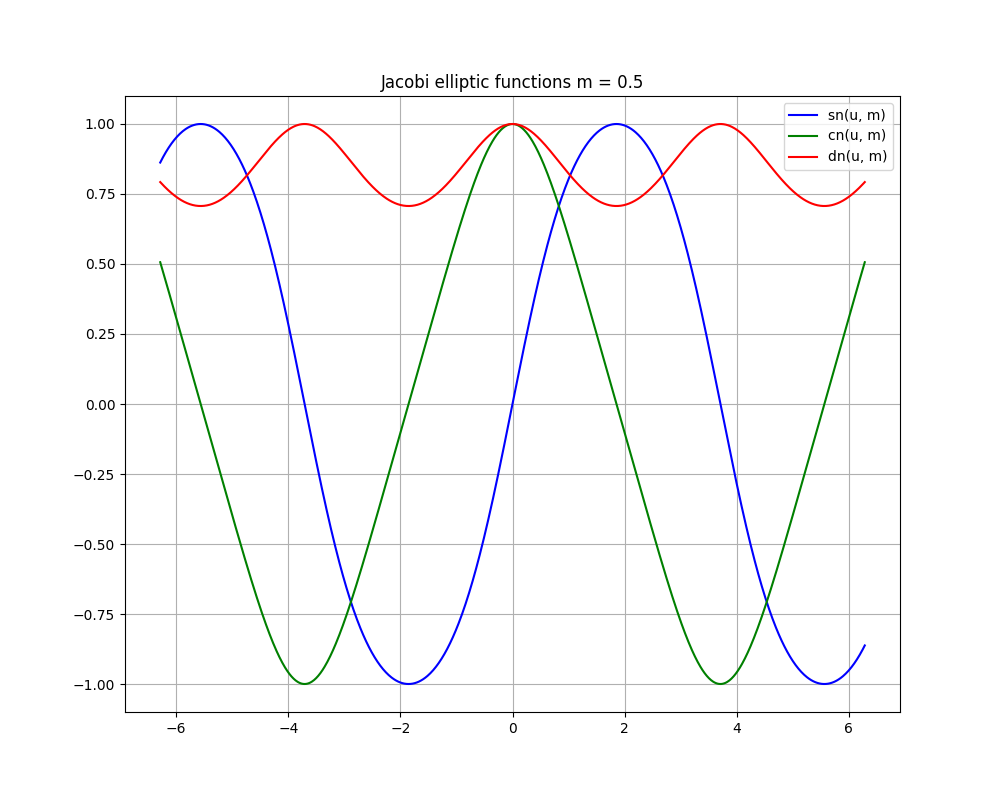
4.参考文献
[1] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」,第1版, 岩波書店, 1975.