第1種ベッセル関数
目次
1.準備
合流型超幾何方程式の1つであるベッセルの微分方程式
\[\frac{\mathrm{d}^2y}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}y}{\mathrm{d}x}+\left(1-\frac{\nu^2}{x^2}\right)=0\tag{1}\]
は、\(x=0\)にただ1つの確定特異点を持つ。一般解は、\(A,B\)を定数として
\[y(x)=A\,J_{\nu}(x)+B\,N_{\nu}(x)\tag{2}\]
と表される。ここで、\(J_{\nu}(x)\):(\nu)次の第1種ベッセル関数 \(N_{\nu}(x)\):\(\nu\)次の第2種ベッセル関数(ノイマン関数)である。\(x\)が実数で\(\nu\)が整数である場合のグラフは以下のようになる。
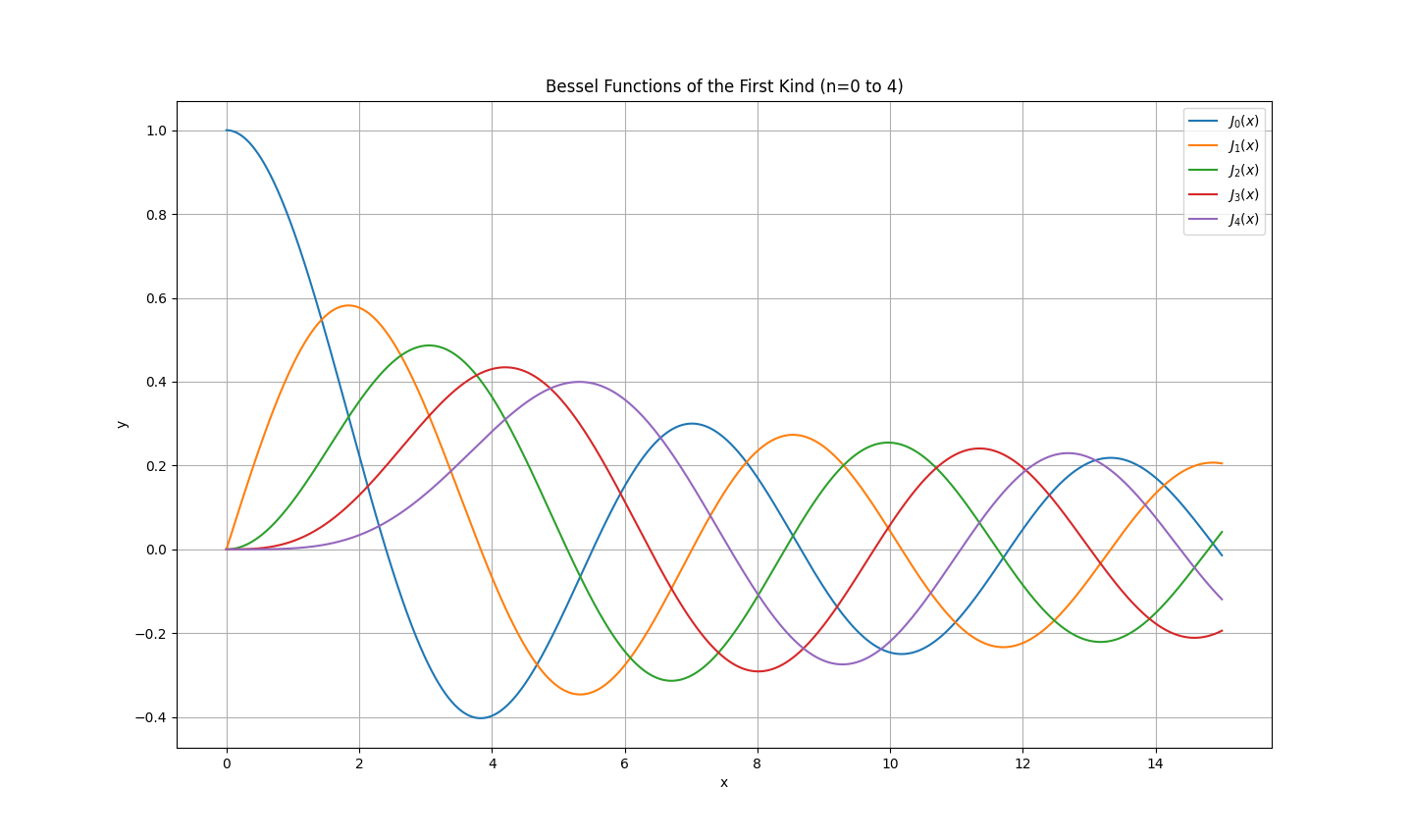
図1 第1種ベッセル関数のグラフ
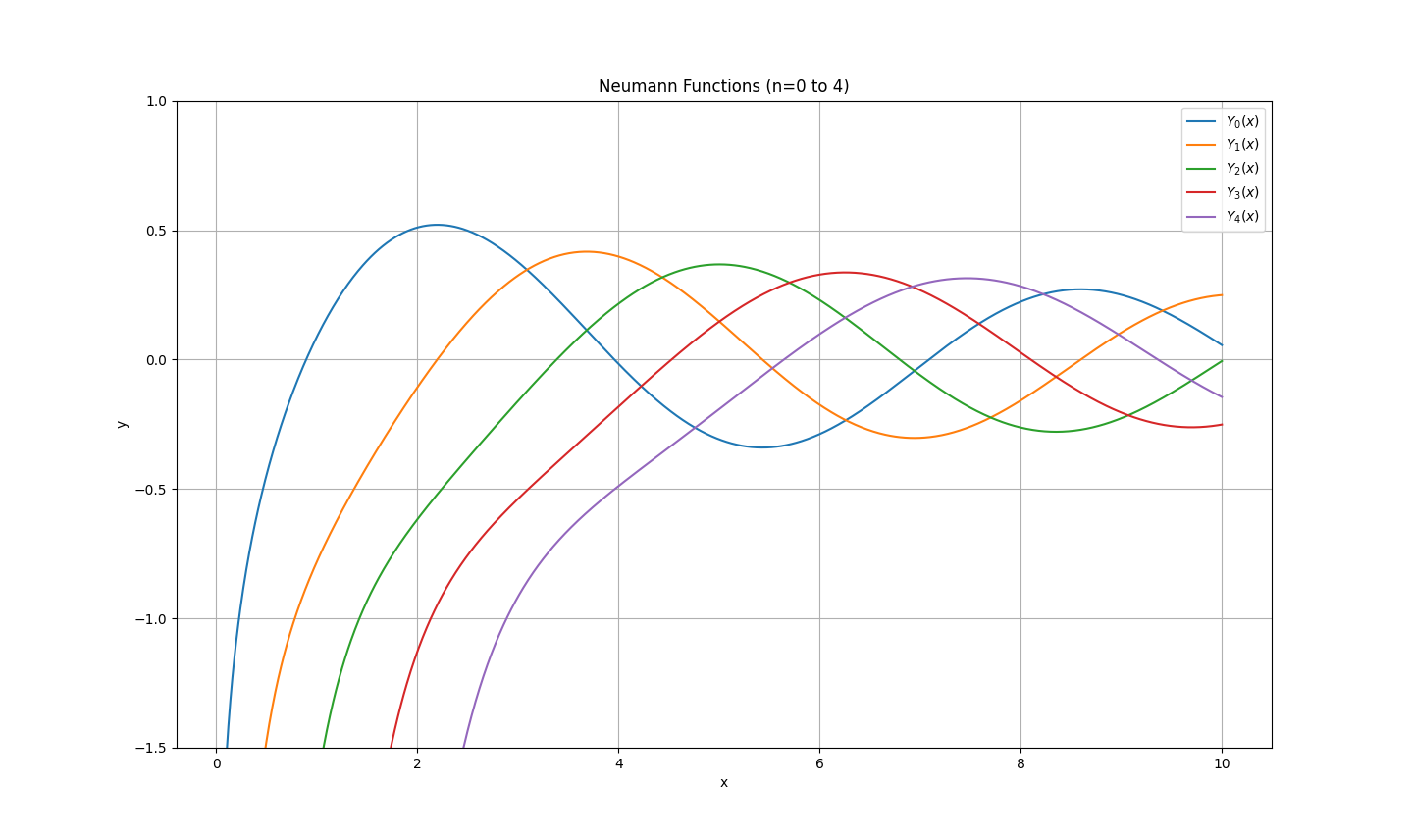
図2 第2種ベッセル関数のグラフ
第2種ベッセル関数の値は\(x\rightarrow 0\)で発散する。第1種ベッセル関数については、0次のみ\(x=0\)における値が非零である。
円筒座標系でラプラス方程式やヘルムホルツ方程式を解くときにベッセルの微分方程式( \(\nu=0\) )がよく出てくる。(たとえば円筒導体における電流密度の半径方向分布)
今回は、実数変数の整数次第1種ベッセルの微分方程式をアナログコンピュータで解いて、第1種ベッセル関数のグラフを描くことを目的とする。(以後\(\nu\)は整数\(n\)として表記することにする。)
重要な公式をここで挙げておく[1]。
(a) 第1種ベッセル関数の級数表示
\[J_n(x)=\left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty}\frac{(-1)^k(x/2)^{2k}}{k!\,\Gamma(n+k+1)}\tag{3}\]
(b) 微分及び漸化式
\[J_0'(x)=-J_1(x)\tag{4}\\\]
\[J_{n}'(x)=\frac{n}{x}J_{n}(x)-J_{n+1}(x)\tag{5}\\\]
\[2\bigl\{J_{n-1}(x)+J_{n+1}(x)\bigr\}=\frac{n}{x}J_{n}(x)\tag{6}\\\]
(5), (6)より
\[J_{n}'(x)=\frac{1}{2}\bigl\{J_{n-1}(x)-J_{n+1}(x)\bigr\}\tag{7}\\\]
2.アナログコンピュータプログラム
ベッセル微分方程式に限らず、最高微分階数項の係数に独立変数が掛かる方程式はアナログ計算機での陽関数法による実装が難しい。時刻0で式の分母が0になり、割算器が飽和するからである。各々の式の形に合わせて適切な実装法を模索せねばならない。
ただ、0次の第1種ベッセル関数のみ得られれば良いのなら、実はそこまで難しくない。
図1のグラフからわかる通り、0次のベッセル関数は初期値1が最大値であり、1次のベッセル関数も最大値は1以下であることから、電圧換算は大変楽である。演算方程式は原方程式そのものを使えばよい。陽関数法で演算する場合、
\begin{eqnarray}\frac{\mathrm{d}^2J_n}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}J_n}{\mathrm{d}x}+\left(1-\frac{n^2}{x^2}\right)J_n=0\\\\ \frac{\mathrm{d}^2J_n}{\mathrm{d}x^2}=-\frac{1}{x}\frac{\mathrm{d}J_n}{\mathrm{d}x}+\frac{n^2}{x^2}J_n-J_n\tag{8}\end{eqnarray}
として\(n=0\)を代入すると
\[\frac{\mathrm{d}^2J_0}{\mathrm{d}x^2}=-\frac{1}{x}\frac{\mathrm{d}J_0}{\mathrm{d}x}-J_0\tag{9}\]
を得る。
しかしながら、このまま割算器で発生させた\(1/x\)を\(\frac{\mathrm{d}J_0}{\mathrm{d}x}\)の項と掛け合わせると、1階微分項の係数が\(x=0\)で発散し、電圧信号としては飽和してしまうので、ひと工夫が必要になる。
式(3)の項別微分により、独立変数原点における微係数を求めると
\[\frac{\mathrm{d}J_n}{\mathrm{d}x}=J_n'(x)=\left\{\begin{array}{ll}\displaystyle 0\;(n\neq 0)\\\\\displaystyle\frac{1}{2}\;(n=1)\end{array}\right.\tag{10}\]
であり、(9)式における信号\(\frac{\mathrm{d}J_0}{\mathrm{d}x}\)は\(x=0\)で分母と分子どちらも0に近く、電圧信号としては有限値をとる。つまり、割算器で\(\frac{\mathrm{d}J_0}{\mathrm{d}x}/x\)を直接生成することで、信号の発散を防ぐことができる。
(4)式から、1次のベッセル関数は0次ベッセル関数の微分値を反転させたものに等しいことがわかるので、式(9)の回路に反転器を追加するのみで求まる。ただし、\(n=1\)のみを生成する場合はこの方法は使えない。なぜなら、(8)式に\(n=1\)を代入した式
\[\frac{\mathrm{d}^2J_1}{\mathrm{d}x^2}=-\frac{1}{x}\frac{\mathrm{d}J_1}{\mathrm{d}x}+\frac{1}{x^2}J_1-J_1\tag{11}\]
において、独立変数原点における微係数 \(\frac{\mathrm{d}J_1(0)}{\mathrm{d}x}\) は0でない値をとり、 \(\frac{\mathrm{d}J_1(0)}{\mathrm{d}x}/x\)の項は飽和する可能性が高い。さらに\(J_1/x^2\)の項もあらたに生じる。
一般の\(n\)の場合も同じような理由で困難が生じる。それ以上に深刻なのが、初期条件の問題である。
整数\(n\)次ベッセル関数の\(x=0\)における値(初期値)として、非零の値が出てくる最初の階数\(k\)は、\(k=n\)の場合である。それ以降は、偶数次であれば偶数階で、奇数次であれば奇数階で非零の初期値が出現する。
以下に、\(J_0(0)=1\)としたときの\(J_n^{(k)}(0)\)の値を示す。
表1 \(n\)次第1種ベッセル関数\(J_n(x)\)の\(x=0\)における\(k\)階微分係数
| n\k | (0) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | 0 | -1/2 | 0 | 3/8 | 0 | -5/16 | 0 | 35/128 | 0 | -63/256 |
| 1 | 0 | 1/2 | 0 | -3/8 | 0 | 5/16 | 0 | -35/128 | 0 | 63/256 | 0 |
| 2 | 0 | 0 | 1/4 | 0 | -1/4 | 0 | 15/64 | 0 | -7/32 | 0 | 105/512 |
| 3 | 0 | 0 | 0 | 1/8 | 0 | -5/32 | 0 | 21/128 | 0 | -21/128 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1/16 | 0 | -3/32 | 0 | 7/64 | 0 | -15/128 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1/32 | 0 | -7/128 | 0 | 9/128 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1/64 | 0 | -1/32 | 0 | 45/1024 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/128 | 0 | -9/512 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/256 | 0 | -5/512 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1/512 | 0 |
このことから、\(n=3\)以上の場合は \(J_n(x)\,,\frac{\mathrm{d}J_n{x}}{\mathrm{d}x}(0)\)の2つの初期条件が両方0になることがわかるので、(11)式では有効な演算回路として構成できない。
(4)の漸化式 \(J_{n-1}'(x)=\frac{(n-1)J_{n-1}(x)}{x}-J_{n}(x)\) を用いて、(n-1)次のベッセル関数とその導関数からn次のベッセル関数を次々と求める手法も考えられるが、その場合割算器の被除数(分子)の\(x=0\)における値が\(n\geq 1\)で0となってしまい、そのうえ\(n\)個もの除算器が必要になる。非線形演算要素の数がコスト面や精度面でのボトルネックになりやすいので、その点からもあまりお薦めできない。
\(n\)次ベッセル関数\(J_n(x)\)のアナログコンピュータによる安定した生成において必要な条件は、
- [初期条件について] \(n\)階微分項\(J_n^{(n)}(x)\)までの\(n\)個の初期条件のうち1つが非零の値をとるように、演算方程式を最低でも\(n+1\)階の常微分方程式とすること。
- [特異点について] できるだけ\(x=0\)で非零の値をとる\(J_n^{(n)}(x)\)項が\(x\)や\(x^2\)で割られないようにすること。
となるだろう。
これらの条件をクリアして\(n\geq 1\)次ベッセル関数を生成する手法としていくつかの演算回路構成法が考案されているので、ここでまとめてみる。
2.1 両辺を\(n\)階微分する方法 ( Binglac & Humo の方法 )
\(n\)次ベッセル関数が満たすベッセル微分方程式
\[x^2\frac{\mathrm{d}^2J_n}{\mathrm{d}x^2}+x\frac{\mathrm{d}J_n}{\mathrm{d}x}+\left(x^2-n^2\right)J_n=0\tag{12}\]
の両辺を独立変数\(x\)について1回微分し、最高階について整理する。
\[-\frac{\mathrm{d}^3J_n}{\mathrm{d}x^3}=\frac{3}{x}\frac{\mathrm{d}^2J_n}{\mathrm{d}x^2}+\left(1+\frac{1-n^2}{x^2}\right)\frac{\mathrm{d}J_n}{\mathrm{d}x}+\frac{2}{x}J_n\tag{13}\]
さらに、\(n=1\)を代入すれば
\[-\frac{\mathrm{d}^3J_1}{\mathrm{d}x^3}=\frac{3}{x}\frac{\mathrm{d}^2J_1}{\mathrm{d}x^2}+\frac{\mathrm{d}J_1}{\mathrm{d}x}+\frac{2}{x}J_1\tag{14}\]
となる。上式は前述の条件を満たすので、これを演算方程式とする回路から \(J_1(x)\)が得られる。
今度は(13)式を2階微分して\(n=2\)を代入し、最高階について整理すると
\[-\frac{\mathrm{d}^4J_2}{\mathrm{d}x^4}=\frac{5}{x}\frac{\mathrm{d}^3J_2}{\mathrm{d}x^3}+\frac{\mathrm{d}^2J_2}{\mathrm{d}x^2}+\frac{4}{x}\frac{\mathrm{d}J_2}{\mathrm{d}x}+\frac{2}{x^2}J_2\tag{15}\]
(16)も条件を満たすので、この式から\(J_2(x)\) が得られる。
一般の\(n\)の場合も同様にして
\[-\frac{\mathrm{d}^{n+2}J_n}{\mathrm{d}x^{n+2}}=\frac{2n+1}{x}\frac{\mathrm{d}^{n+1}J_n}{\mathrm{d}x^{n+1}}+\frac{\mathrm{d}^{n}J_n}{\mathrm{d}x^{n}}+\frac{2n}{x}\frac{\mathrm{d}^{(n-1)}J_n}{\mathrm{d}x^{n-1}}+\frac{n(n-1)}{x^2}\frac{\mathrm{d}^{n-2}J_n}{\mathrm{d}x^{n-2}}\tag{16}\]
(16)式をもとに演算方程式をつくると
\begin{eqnarray}-\frac{{a_{\tau}}^{n+2}}{a_J}\frac{\mathrm{d}^{n+2}J_n}{\mathrm{d}{\tau}^{n+2}}&=&\frac{{a_{\tau}}^{n+1}}{a_J}\frac{(2n+1){a_{T}}}{T}\frac{\mathrm{d}^{n+1}J_n}{\mathrm{d}{\tau}^{n+1}}+\frac{{a_{\tau}}^n}{a_J}\frac{\mathrm{d}^{n}J_n}{\mathrm{d}{\tau}^{n}}+2n\,\frac{{a_{\tau}}^{n-1}}{a_J}\frac{a_{T}}{T}\frac{\mathrm{d}^{n-1}J_n}{\mathrm{d}{\tau}^{n-1}}+n(n-1)\frac{{a_{\tau}}^{n-2}}{a_J}\frac{ {a_T}^2}{T^2}\frac{\mathrm{d}^{n-2}J_n}{\mathrm{d}{\tau}^{n-2}}\\\\-{a_{\tau}}^{n+2}\frac{\mathrm{d}^{n+2}J_n}{\mathrm{d}{\tau}^{n+2}}&=&{a_{\tau}}^{n+1}\frac{2n+1}{{T}/{a_{T}}}\frac{\mathrm{d}^{n+1}J_n}{\mathrm{d}{\tau}^{n+1}}+{a_{\tau}}^n\frac{\mathrm{d}^{n}J_n}{\mathrm{d}{\tau}^{n}}+{a_{\tau}}^{n-1}\frac{2n}{{T}/{ a_{T}}}\frac{\mathrm{d}^{n-1}J_n}{\mathrm{d}{\tau}^{n-1}}+{a_{\tau}}^{n-2}\frac{n(n-1)}{{T^2}/{{a_T}^2}}\frac{\mathrm{d}^{n-2}J_n}{\mathrm{d}{\tau}^{n-2}}\\\\-\frac{\mathrm{d}^{n+2}J_n}{\mathrm{d}{\tau}^{n+2}}&=&\frac{1}{{a_{\tau}}^2}\frac{\mathrm{d}^{n}J_n}{\mathrm{d}{\tau}^{n}}+\frac{1}{T}\left[(2n+1)\frac{a_{T}}{a_{\tau}}\frac{\mathrm{d}^{n+1}J_n}{\mathrm{d}{\tau}^{n+1}}+2n\frac{a_{T}}{a_{\tau}}\frac{1}{{a_{\tau}^2}}\frac{\mathrm{d}^{n-1}J_n}{\mathrm{d}{\tau}^{n-1}}+\frac{1}{T}\left\{n(n-1)\frac{{a_{T}}^2}{{a_{\tau}}^2}\frac{1}{{a_{\tau}}^2}\frac{\mathrm{d}^{n-2}J_n}{\mathrm{d}{\tau}^{n-2}}\right\}\right]\tag{17}\end{eqnarray}
(17)式が一般の\(n\)の場合の演算方程式となる。
この方法は非零の初期値を持つ\(n\)階微分項が独立変数で割られないというメリットがある。さらに、初期条件として非零の値が必ず設定できるのが特徴であり、最初に出てくる非零初期条件
\[J_n^{(k)}=\left(\frac{1}{2}\right)^n\, J_n(0)\,\delta_{n,j}\tag{18}\]
(ただし \(\delta_{n,j}\)はクロネッカーのデルタ)を第2の積分器に入力すればよいだけである。
無論欠点を完全に廃せたわけではなく、初期値が0の項の除算 (0÷0) は避けられない。ただし、除算器出力が戻される積分器が1つのみであるため、\(n\)が大きいほど多くの積分器を通過し誤差は「ある程度は」平滑低減されることが期待できる。一番最初に示した\(J_{0}(x)\)の演算回路中の時間微分項を用いて\(J_{1}(x)\)を得るような回路では、除算出力から積分器1つ分しか離れてない箇所の信号を引っ張り出すため、誤差が無視できなかった。以上のことから、Binglac と Humo の方法は、その従来手法よりは優れていると考えてよいだろう。
\(n\)次の第1種ベッセル関数を発生させるのに必要な積分器は\(n+3\)個である。
本方式の詳細については文献 [3] を参照して頂きたい。
2.2 媒介変数法 (Hausnerの方法)
微分方程式の独立変数を従属変数(媒介変数)にして、式中の特異点を除去する方法である 。0次および1次のベッセル関数の生成で使える。
原方程式の従属変数を\(y\)、独立変数を\(\theta\)とおく。\(\theta\geq0\)の範囲で\(n\)次ベッセル関数の解を得ることを考えよう。
\[\theta^2\frac{\mathrm{d}^2y}{\mathrm{d}\theta^2}+\theta\frac{\mathrm{d}y}{\mathrm{d}\theta}+\bigl(\theta^2-n^2\bigr)J_n=0\tag{19}\]
\(\frac{\mathrm{d}y}{\mathrm{d}\theta}=x\)として、連立1階常微分方程式にすると
\[\left\{\begin{array}{ll}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}\theta}=x\\\\\displaystyle \frac{\mathrm{d}x}{\mathrm{d}\theta}=\frac{\left(n^2-\theta^2\right)y+\theta{x}}{\theta^2}\end{array}\right.\tag{20}\]
ここで、計算機上で演算時間\(\tau\)とする変数 \(t\) を導入し、真の独立変数とする。\(\theta\)はただ\(t\)についての関数であるとする。(\(\theta\)と\(t\)の関係式はまだ決定されない)
(19)の2式左辺に対し連鎖律を適用し、\(t\)についての微分に直すと
\[\left\{\begin{array}{ll}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=x\frac{\mathrm{d}\theta}{\mathrm{d}t}\\\\\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\frac{\left(n^2-\theta^2\right)y+\theta{x}}{\theta^2}\frac{\mathrm{d}\theta}{\mathrm{d}t}\end{array}\right.\tag{21}\]
(20)の関係性から、\(t\)と\(\theta\)の関係を
\[\frac{\mathrm{d}\theta}{\mathrm{d}t}=-\xi\,\theta^2\tag{22}\]
として定めれば特異点が消えて都合がよいことがわかる。ただし、\(\xi\)は定数。
\[\left\{\begin{array}{lll}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}&=&\xi\theta^2 x\\\\\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}&=&\frac{\left(n^2-\theta^2\right)y+\theta{x}}{\theta^2}\xi\theta^2\\\\\displaystyle\frac{\mathrm{d}\theta}{\mathrm{d}t}&=&\xi\theta^2\end{array}\right.\]
\[\therefore\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{ccc}y\\\\x\\\\\theta\end{array}\right)=\xi\left(\begin{array}{ccc}\displaystyle\theta^2 x\\\\\displaystyle\left(n^2-\theta^2\right)y+\theta{x}\\\\\displaystyle\theta^2\end{array}\right)\tag{23}\]
(21)式の作る三次元空間上の軌道\(\{y(t)\,,x(t)\,,\theta(t)\}\)を\((x,\theta)\)平面に投影したものが(19)式の解となる。実定数\(\xi\)の正負は解軌道上の点が演算時間\(t\)(演算変数としては\(\tau\)と表記する)が増大するにあたり軌道上をどちらの方向に動くかを決定する。もし正ならば \(\theta\rightarrow\infty\,(t\rightarrow\infty)\)となり、負であるならば \(\theta\rightarrow 0\,(t\rightarrow\infty)\)となるよう動く。
この効果は時間換算係数\(a_{\tau}\)の符号の正負の効果と同様であり、絶対値は積分時定数に影響するので、\(\xi\)は時間換算係数であると解釈することもできる。
\(\xi=1\)と定めると
\[\left\{\begin{array}{ll]}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=\theta^2x\\\\\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\left(n^2-\theta^2\right)y+\theta{x}\\\\\displaystyle\frac{\mathrm{d}\theta}{\mathrm{d}t}=\theta^2\end{array}\right.\tag{24}\]
(22)を演算回路として実現すれば、除算は不要になる。かりに\(\xi\)を負にすると、 \(\theta\rightarrow 0\,(t\rightarrow\infty)\)という「逆行解」が得られることに注意。逆に考えれば、初期条件ではなく\(\theta=0\)以外での境界条件でベッセルの微分方程式を解きたい場合には最適な手法と言えるだろう。
なお、ルジャンドルの微分方程式もこの方法で解ける。
本方式について詳しく知りたい方は文献 [4] [5] を参照して頂きたい。
2.3 電流加算点電位をダミー変数とする方法 (黒川らの方法)
演算の理論 2.6節で述べた方法の応用である。文献[2]のp.90-p.91でも言及されている。
(1) \(n\geq{1}\)のとき
ベッセル微分方程式の右辺の0を\((k+1)\) 階微分項としておく。ただし、非負整数 \(k\) は、\(n=1,2\)のとき\(3\)、\(n\geq{4}\)のとき\(n\)とする。独立変数をtとすると
\[t^2\frac{\mathrm{d}^2J_n}{\mathrm{d}t^2}+t\frac{\mathrm{d}J_n}{\mathrm{d}t}+\bigl(t^2-n^2\bigr)J_n=-\frac{1}{\mu}\frac{\mathrm{d}^{k+1}J_n}{\mathrm{d}t^{k+1}}\tag{25}\]
ここで\(\mu\)はオープンループアンプのゲインであり、非常に大きい値をとるとする。
(2) \(n=0\)の場合
原方程式の両辺を独立変数で割った式をもとに、
\[t\frac{\mathrm{d}^2J_0}{\mathrm{d}t^2}+\frac{\mathrm{d}J_0}{\mathrm{d}t}+t\,J_0=-\frac{1}{\mu}\frac{\mathrm{d}^{3}J_0}{\mathrm{d}t^{3}}\tag{26}\]
とすればよい。
このように、形式的に\(k+1\)階微分項を高利得増幅器のオープンゲインで除した項を導入することで、3次以上の場合でも非零の初期条件を確保しつつ、2階微分項について陽に解くことなく実装できる。演算回路の構成もわかりやすいうえ、除算器が不要であり、なおかつ時間換算係数と電圧換算係数の設定を独立して行えることが利点である。ハイブリッド計算方式に最適な手法と言える。もちろん、ベッセル微分方程式以外にも一般に適用可能な手法である。
最大の利点は、換算係数を変えずに回路から除算器を排することができ、精度のよい演算が行えることにある。係数器の設定の手間も少ない。以上のことから、本方法が2.1および2.2節の手法より優れているといえよう。
この方法の詳細は文献 [6] (US Patent 3652843A) を参照して頂きたい。
※ 以上3つの他にも、独立変数を\(x=\varepsilon e^{-\beta{t}}\,,(\varepsilon\approx 0,\beta\gg 0)\)として時間原点近傍でのゼロ除算を回避する近似方法、式をもとに評価関数を設定し、最急降下のプログラムを行う方法などがあるが、ここでは省略する。
3.結果
3.1 Binglac & Humo の方法
まず、Binglacの論文通りに実装した結果を示す。\(a_{\tau}=1\)、\(a_{T}=1/10\)である。
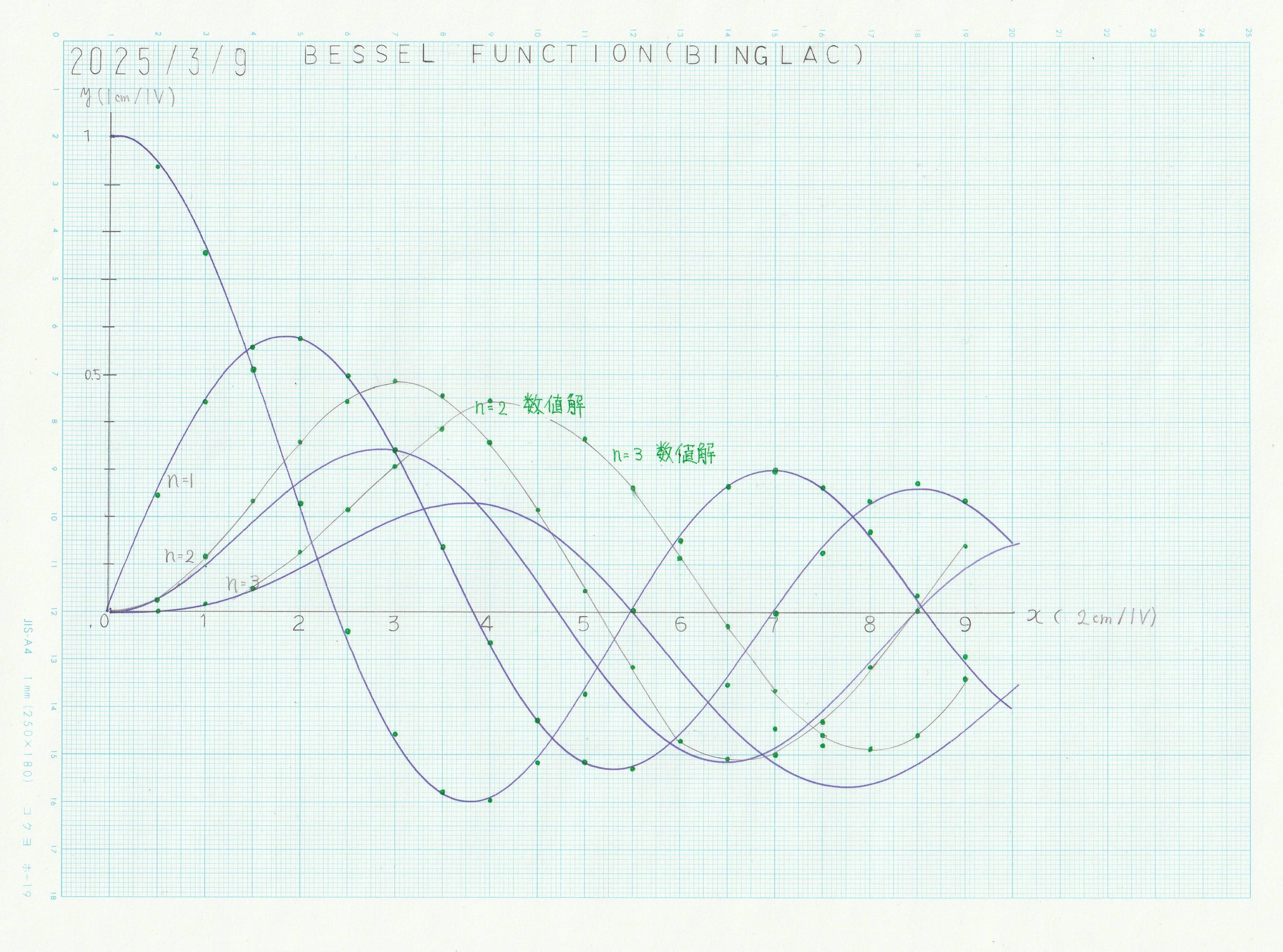
図3 Binglacの方法によるベッセル関数の演算結果
数値計算による解を緑の点でプロットした。両者を比較すると、\(n=0,n=1\) でかなり精密な解が得られているが、\(n=2\)以上では誤差が著しく出ていることがわかる。詳しく調べると、回路中の最高階項に入力される高利得増幅器の波形が、\(t=0\)近傍でかなり暴れていることが判明した。対策として、アナログコンピュータにあらかじめ設けて置いたデジタル信号駆動型のアナログスイッチ回路と、比較器の2値出力信号を利用して、演算開始後一定期間は最高階積分器の入力は\(J_n\)のみ帰還させ、高利得増幅器(除算器)の出力はその後に投入するような結線プログラムを試みたが、多少の改善は見られたものの実用には至らなかった。
以上の結果を鑑み、より精度の良い結果を得るため従来の除算器を最急降下法を利用した除算回路に置き換えることとした。
\(a_{T}=1/10\), \(a_{\tau}=1\) としたときの、最急降下除算を利用した3次ベッセル微分方程式の演算回路を図に示す。
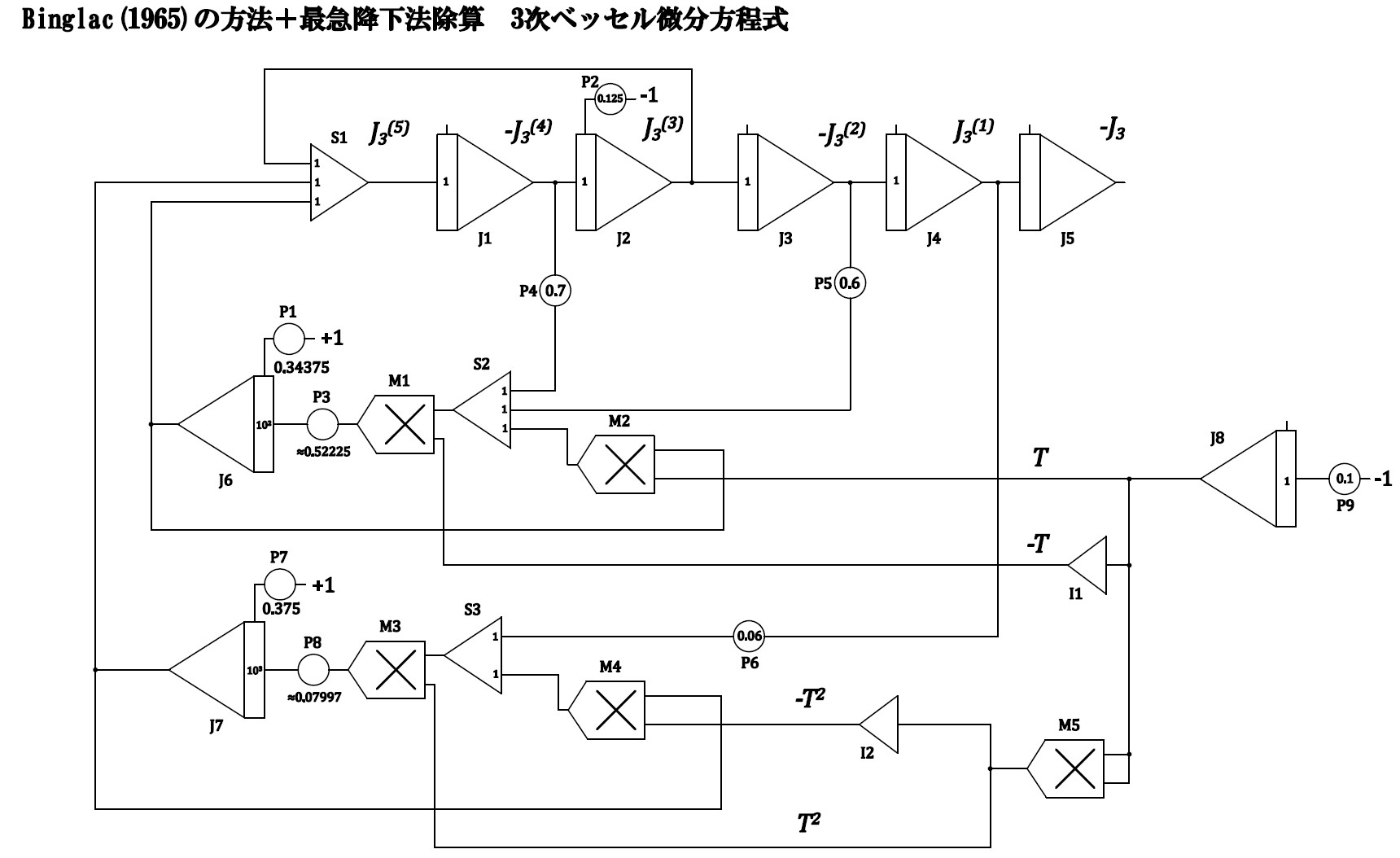
図4 n=3の場合の演算回路
除算の初期値は別個に設定する必要がある。私は級数展開して極限をとり初期値を計算した。最急降下のゲインは数学的には大きくとった方が収束がよいのだが、計算機回路的な制約上、大きすぎるのも誤差の元となるから最適値を探る必要がある。
\(n=0\) から \(n=3\) の場合の低速モードにおける演算結果を次に示す。
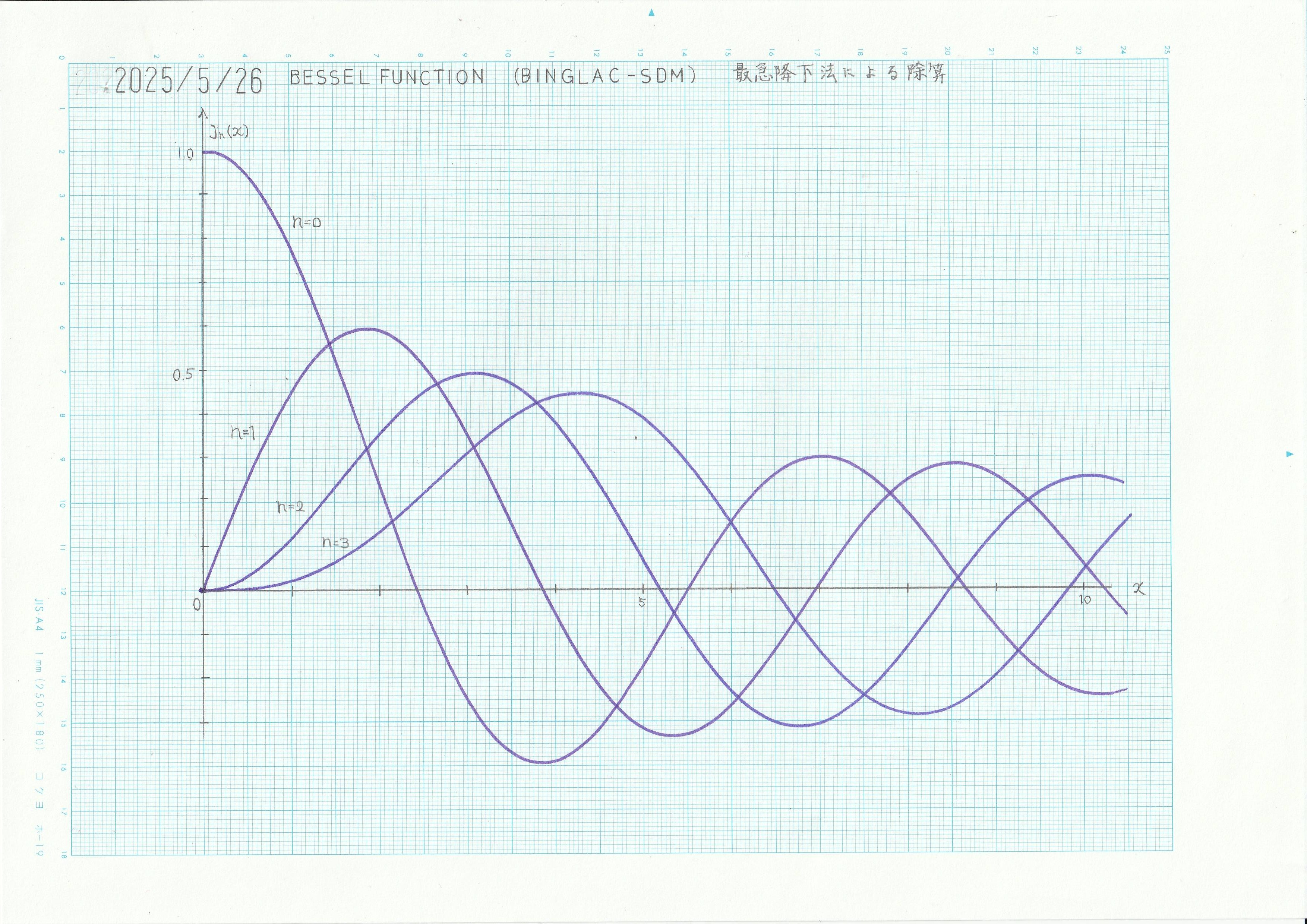
図5 演算結果 (Binglac + 最急降下法による除算)
\(n=3\) まではかなり精確な解を得られた。しかし、より高次の場合は時間が経つと誤差が無視できなくなった。
回路からわかる通り、3次以上では解関数を開ループによる単純縦続積分で求めるので、その積分で定常誤差が累積して現れてしまうことが原因と思われる。
3.2 黒川らの方法
特許文献[6]の方法に忠実に従った場合の結果を示す。
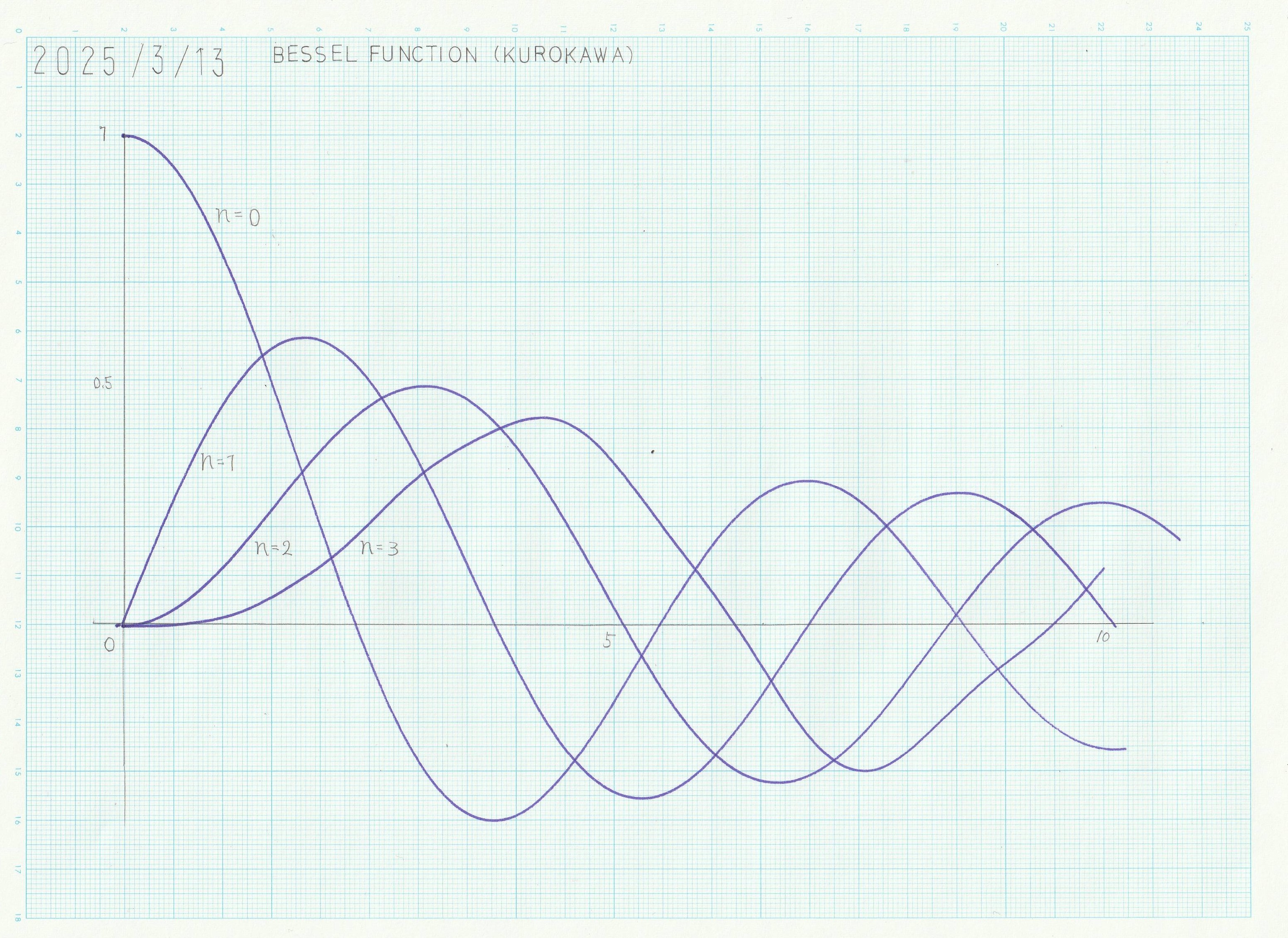
図6 黒川らの方法によるベッセル関数の演算結果
0次と1次のベッセル関数については正確な解を出しているが、\(n=3\)の波形はところどころに歪が生じている。こちらも、高利得増幅器の出力が超低周波で振動していたことが直接の原因である。
そこで文献[8]を参考に、高利得増幅器の利得を係数器で微調整できるようにしてみた。アンプのオープンゲインが有限であることに起因する誤差を補正することが目的である。その場合の \(\ddot{y(t)}+y(t)=0\)を解くサークルテスト回路と、高速モードにおける演算結果を図に示す。
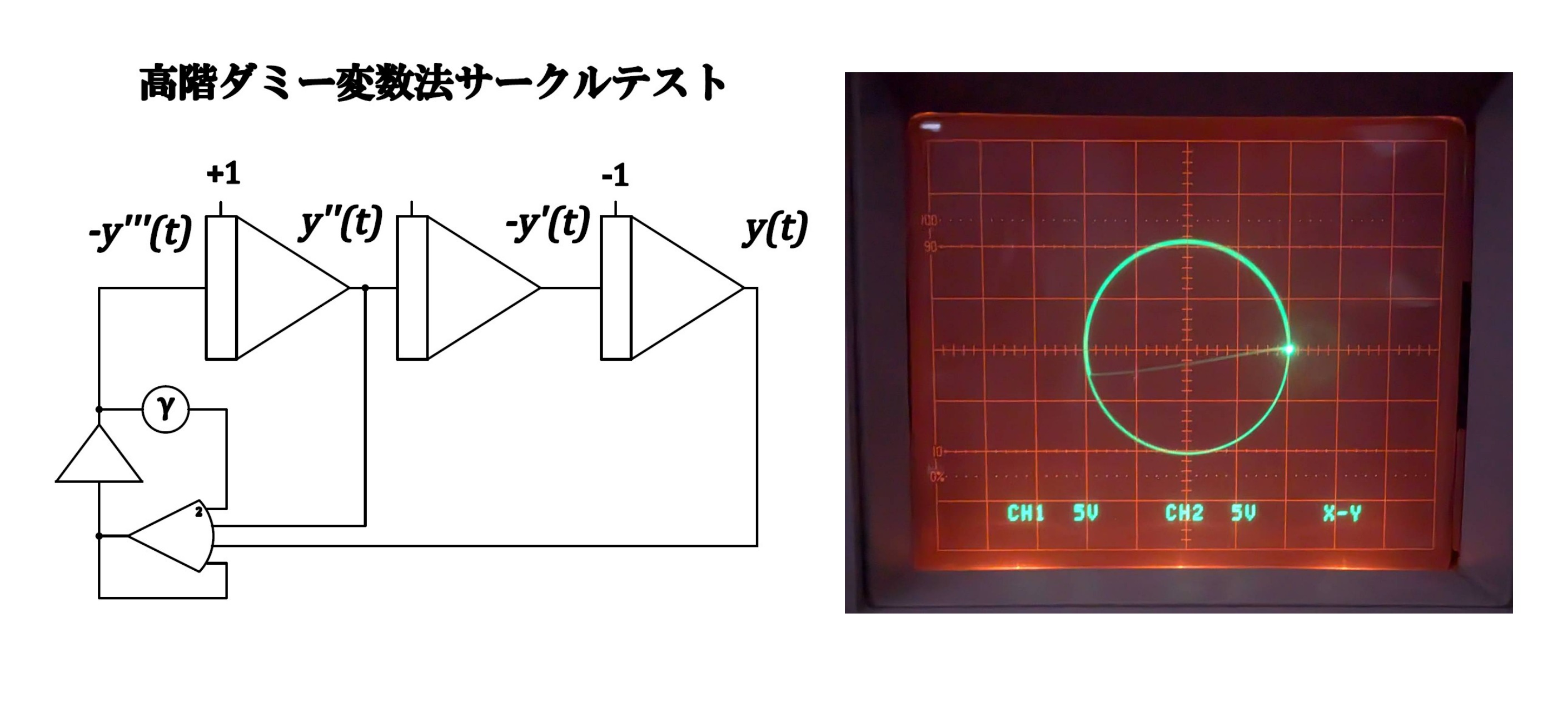
図7 サークルテスト
係数器の \(\gamma\) の値を0.5前後で微調節する。
以上の補正を踏まえた3次のベッセル微分方程式演算回路は以下のようになる。引き続き \(a_{\tau}=1,\,a_{T}=0.1\) とした。
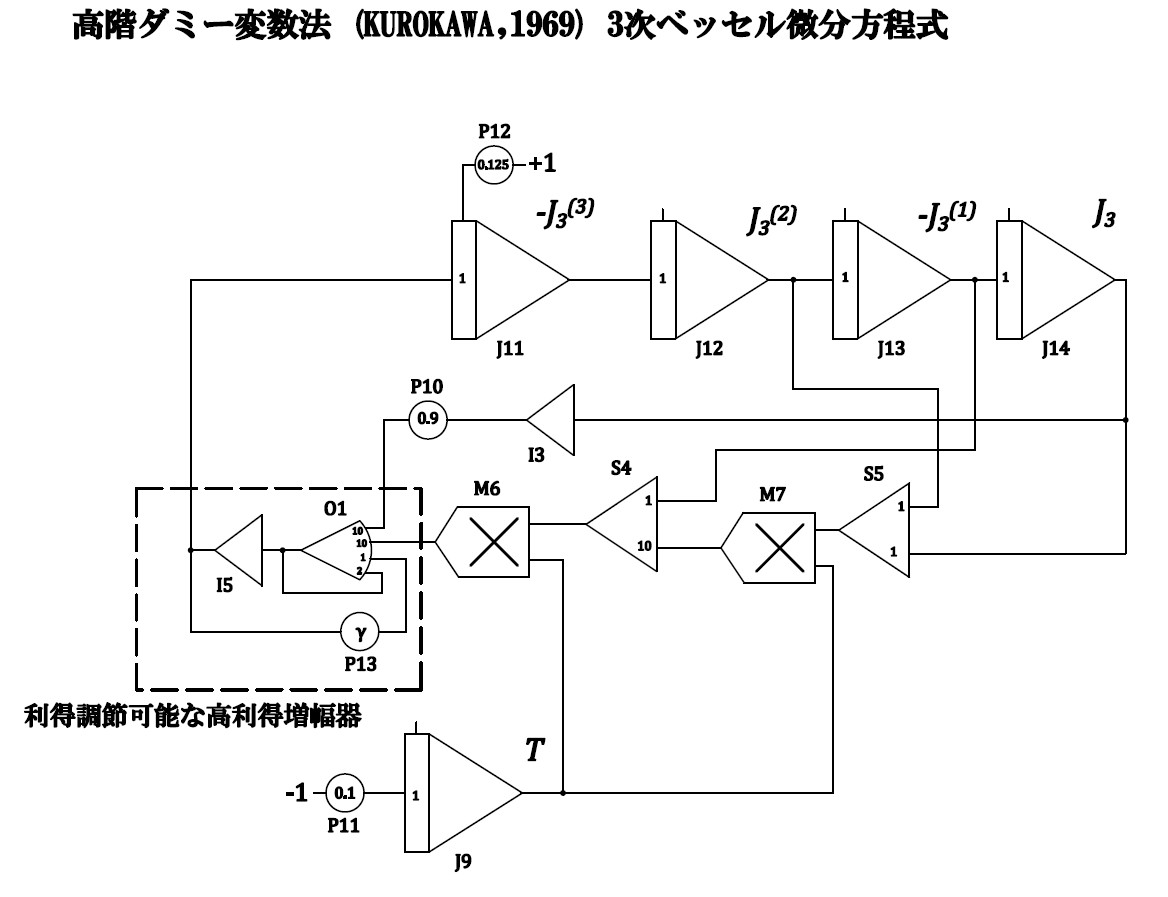
図8 \(n=3\)の場合の演算回路(黒川らによる方法)
\(n=0\)から\(n=3\)の演算結果を以下に示す。
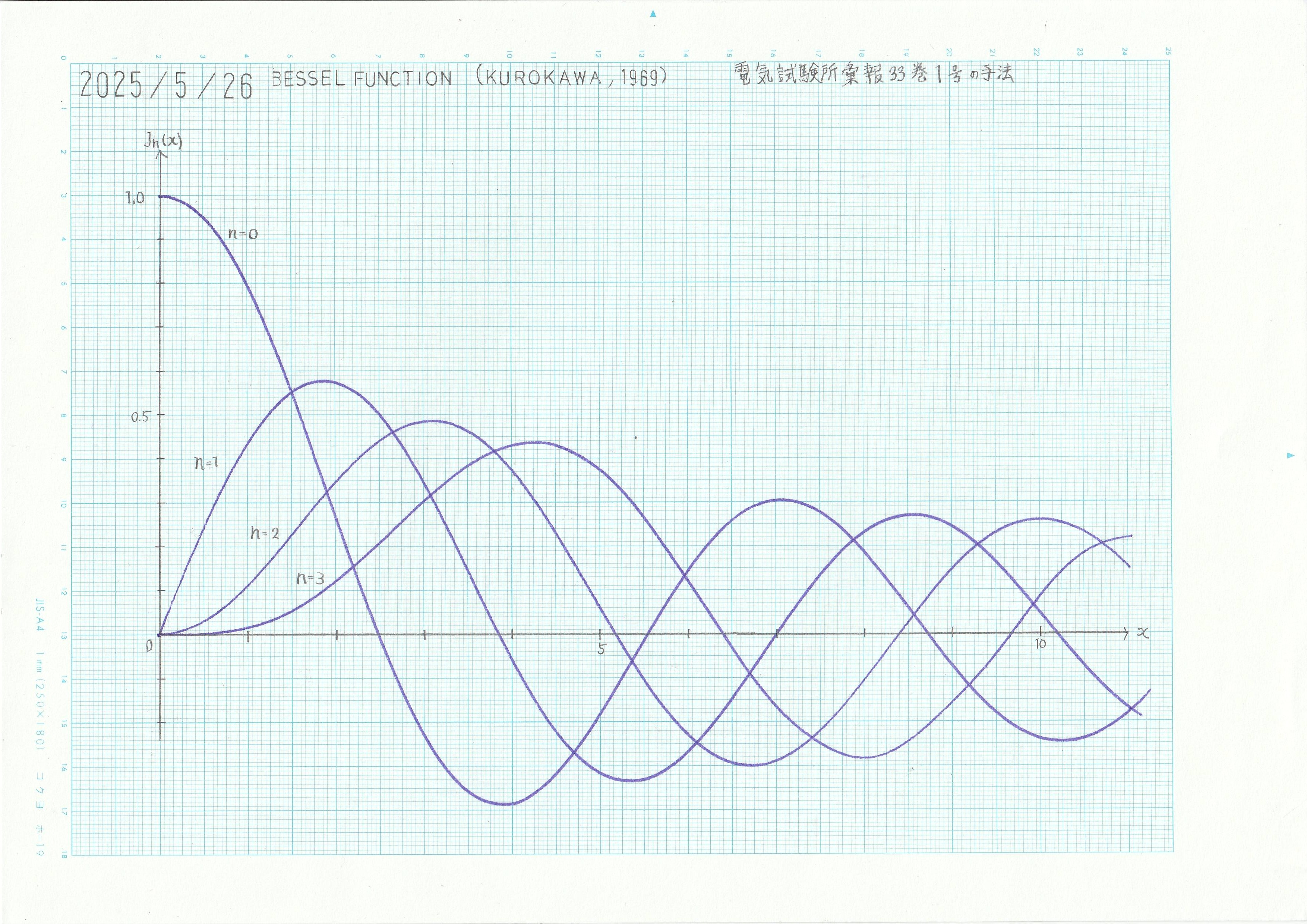
図9 黒川らの方法による演算結果(利得補正あり)
少なくとも3次までは高精度な解が得られる。
しかし、これ以上高次の解では誤差が目立つ。Binglacの方法と異なり開ループ積分による誤差は生じえないが、次数が大きくなるにしたがい、ループ内の縦続積分器個数が多くなるうえに、 \(t=0\) で非零の値をとる積分項が1つだけという条件であるから、回路中唯一の安定負帰還ループ(図8中でP10を含むメインループ)の帰還量が演算開始後しばらくたったあとも小さいままであり、そのあいだに微小擾乱が拡大することが原因と考える。
4.参考文献
[1] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」第1版, 岩波書店, 1975.
[2] 藤田広一. 「アナログ計算機のプログラム」第12版, 昭晃堂, 1978.
[3] S. P. Binglac, E. A. Humo. "Analog Computer Generation of Bessel Functions of Arbitrary Order" IEEE TRANSACTIONS ON ELECTRONIC COMPUTERS. VOL. EC-14, NO. 6, 1965.
[4] A. Hausner, "Parametric Techniques for Eliminating Division and Treating Singularities in Computer Solutions of Ordinary Differential Equations," in IRE Transactions on Electronic Computers, vol. EC-11, no. 1, pp. 42-45, Feb. 1962.
[5] T. A. Newton, "Some Parametric Techniques in the Analog Solution of Ordinary Differential Equations," in IEEE Transactions on Computers, vol. C-24, no. 1, pp. 1-8, Jan. 1975.
[6] Kazuo Kurokawa, Ikuo Matsuda. Setup system in analog computer. US Patent 3652843A. Mar. 28, 1972. https://patents.google.com/patent/US3652843
[7] 森 繁雄, 芹沢 正三, 安藤 四郎. 「工業基礎数学 微分方程式」第10版, 東京書籍 ,1986.
[8] 松田 郁夫, 黒川 一夫. 「ハイブリッド計算システムにおける計算方式 ーハイブリッド計算機としてのアナログ演算部の計算方式ー」電気試験所彙報, 1969, 第33巻1号, p.22-p.35