dy/dx=P(x,y)/Q(x,y)で表される微分方程式
目次
- 分数形の1階微分方程式
- \(\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{-1.8x-3y}{x+2y}\)
- \(\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{3(x^2-1)}{8y}\)
- \(\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x^2-y}{y^2-x}\)
- \(\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x^3-x}{y^3-y}\)
- \(\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{-6y-x(3+x)}{y}\)
- 参考文献
1.分数形の1階微分方程式
このような微分方程式は解析解が容易に得られる場合が多いが、アナログ計算機によるシミュレーションも大変興味深いので今回取り扱うこととした。
さまざまな初期条件で微分方程式を解いて、低速モードで解曲線群（積分曲線）を描出することを目標とする。
2.\(\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{-1.8x-3y}{x+2y}\)
微分方程式
\[\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{-1.8x-3y}{x+2y}\tag{1}\]
を解析する。媒介変数として時間 \(t\) を導入すると、
\begin{cases}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}&=-1.8x-3y\\\\\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}&=x+2y\tag{2}\end{cases}
となり、単なる2元連立1階線形微分方程式になる。電圧換算係数、時間換算係数をすべて1としてよいので、原方程式が直ちに演算方程式となる。演算回路は以下の通り。
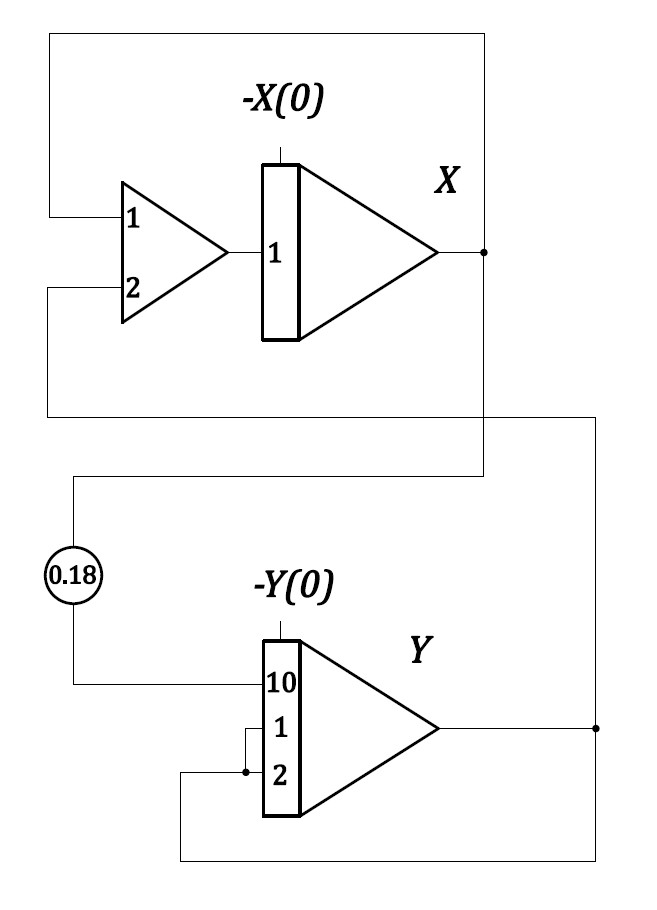
図1 式(2)の演算回路
\(x\) と \(y\) の各信号をX-Yレコーダに入力して解曲線を描出したもの(左)と厳密解(右)を以下の図である。
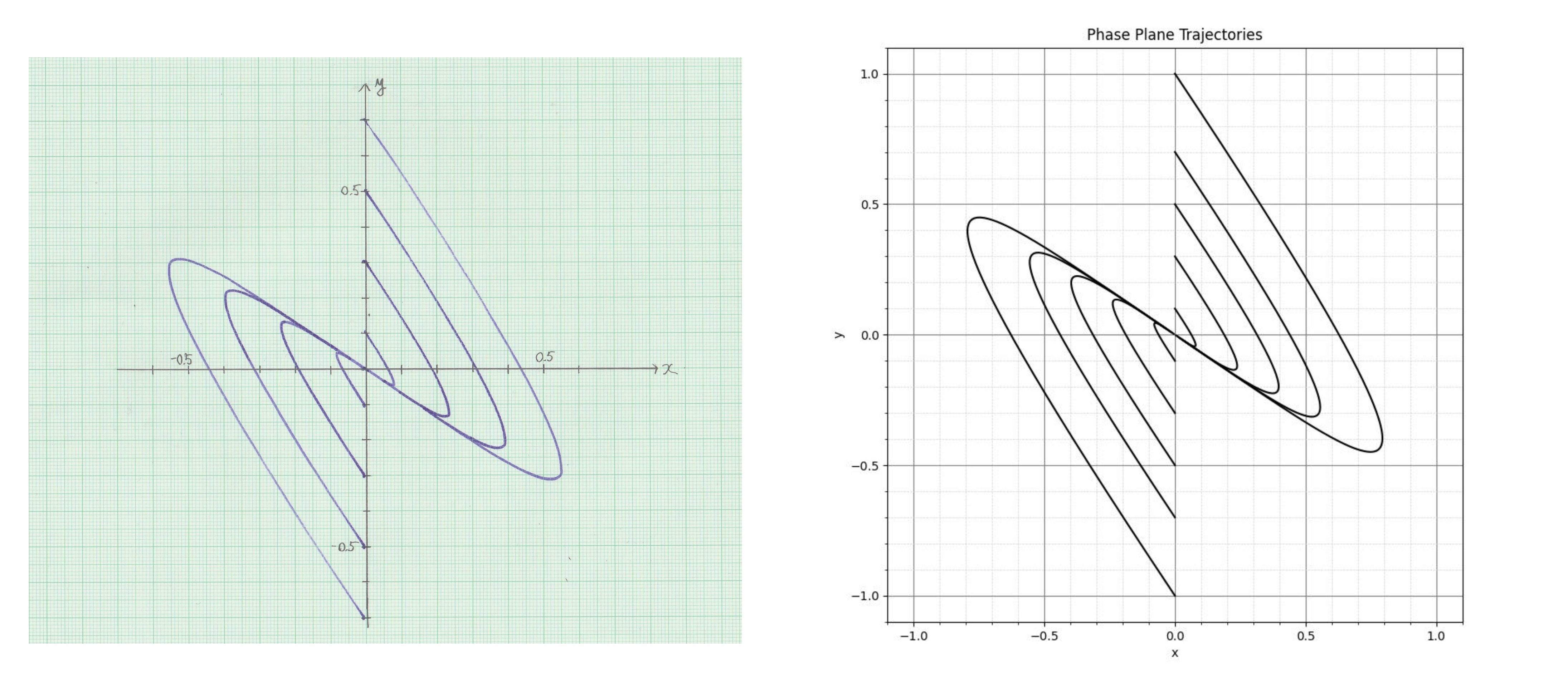
図2 式(2)の積分曲線（アナログ計算機解と厳密解）
原点は微分値が全て0になる臨界点（平衡点）であるわけだが、系のヤコビ行列は
\[J=\begin{bmatrix}1&2\\-1.8&-3\end{bmatrix}\tag{3}\]
であり、その固有値は \(-1\pm\sqrt{0.4}\) である。これは２つとも負の実数であるから、この系の原点は安定ノード（安定結節点）である。つまり解は振動することなく（相平面上で渦を巻くことなく）0に漸近する。
3.\(\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{3(x^2-1)}{8y}\)
微分方程式
\[\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{3(x^2-1)}{8y}\tag{4}\]
を解析する。媒介変数\(t\)を導入すると、
\begin{cases}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}&=3(x^2-1)\\\\\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}&=8y\tag{5}\end{cases}
となる。電圧換算係数を \(a_{X}=1/5\), \(a_{Y}=1/5\)とし、各変数の1階微分の電圧換算係数と共通させる。時間換算係数はそのまま \(a_{\tau}\) とおく。演算方程式は
\begin{cases}\displaystyle{a_{\tau}}\frac{\mathrm{d}Y}{\mathrm{d}\tau}&=15X^2-0.6\\\\\displaystyle{a_{\tau}}\frac{\mathrm{d}X}{\mathrm{d}\tau}&=8Y\tag{6}\end{cases}
となることがわかる。初期条件によって軌道上を動く速さが異なるため、時間換算係数はその都度変えることが望ましい。\(a_{\tau}=1\) の場合の演算回路とアナログ計算機解は以下のようになる。
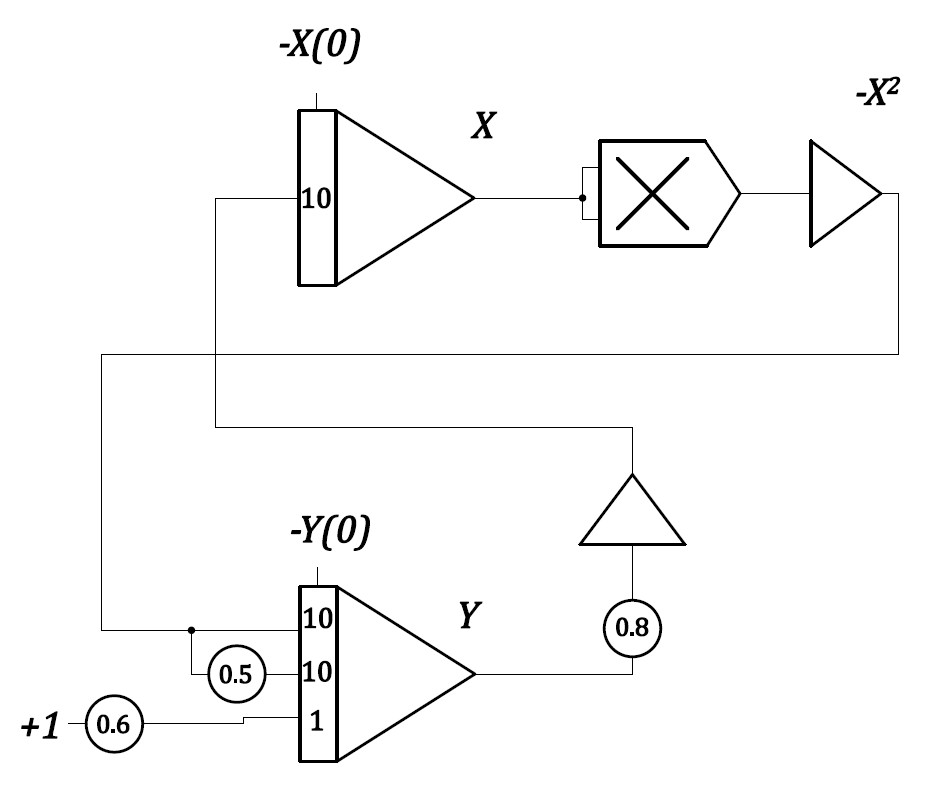
図 3 式(4)の演算回路
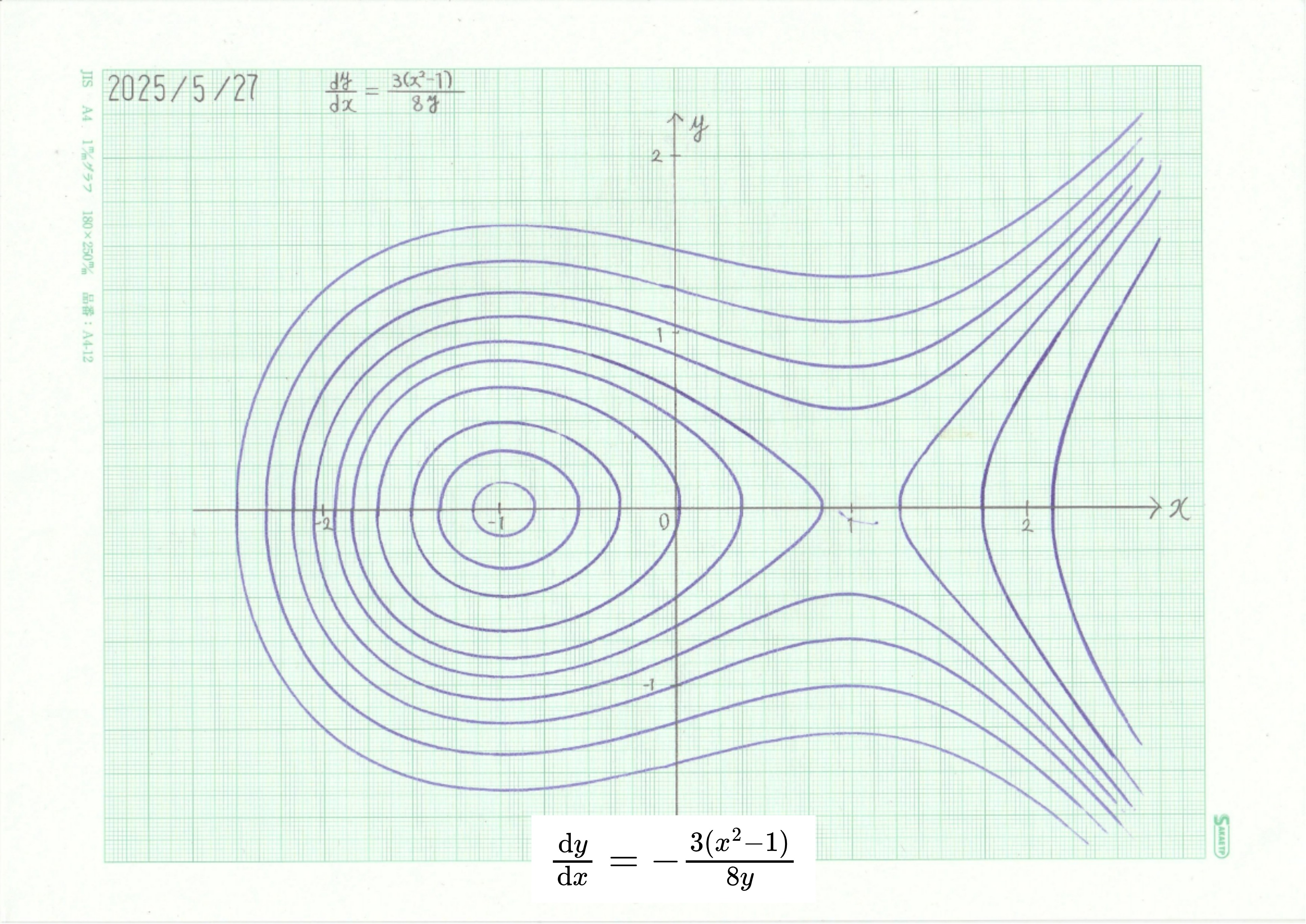
図 4 式(4)の積分曲線
\((x,y)=(1,0),\,(-1,0)\) は微分値が全て0になる臨界点（平衡点）である。系のヤコビ行列は
\[J=\begin{bmatrix}0&8\\6x&0\end{bmatrix}\tag{7}\]
と計算できる。\((1,0)\)での固有値は \(\pm\,4\sqrt{3}\) であり、これは正と負の実数であるから、鞍点。いっぽう、\((-1,0)\)での固有値は \(\pm\,4\sqrt{3}i\) であり、互いに共役な純虚数であるので中心点（渦点）である。
特異点近傍では積分器入力が極小になるため回路全体で誤差が極めて大きくなる。原理的には、特異点ちょうどを通過する解曲線を描こうとすると、途中で積分動作が停止するはずである。実際の場合は積分器入力は完全に0にならず、きわめて微小なノイズにより別の軌道にシフトしてしまうため、臨界点を通過する積分曲線の直接描出はできないが、きわめて近い箇所を通過させてあとから外挿修正することとなる。
各積分器の入力信号の符号を全て反転させると、時間換算係数を負の値にしたことと同じになり、軌道上を動く向きも逆転する。周期解が現れる場合は、初期点から1周させるよりも、積分器の符号を変えることで右回り、左回りで半周させて軌道を完成する方が累積誤差を小さくできる。
4.\(\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x^2-y}{y^2-x}\)
微分方程式
\[\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x^2-y}{y^2-x}\tag{8}\]
を解析する。
媒介変数\(t\)を導入すると、
\begin{cases}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}&=x^2-y\\\\\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}&=-y^2+x\tag{9}\end{cases}
\(a_{X}=a_{Y}=1/4\) とすると、演算方程式は以下のようになる。
\begin{cases}\displaystyle{a_{\tau}}\frac{\mathrm{d}Y}{\mathrm{d}\tau}&=4X^2-Y\\\\\displaystyle{a_{\tau}}\frac{\mathrm{d}X}{\mathrm{d}\tau}&=-4Y^2+X\tag{10}\end{cases}
演算回路とアナログ計算機解を以下に示す。
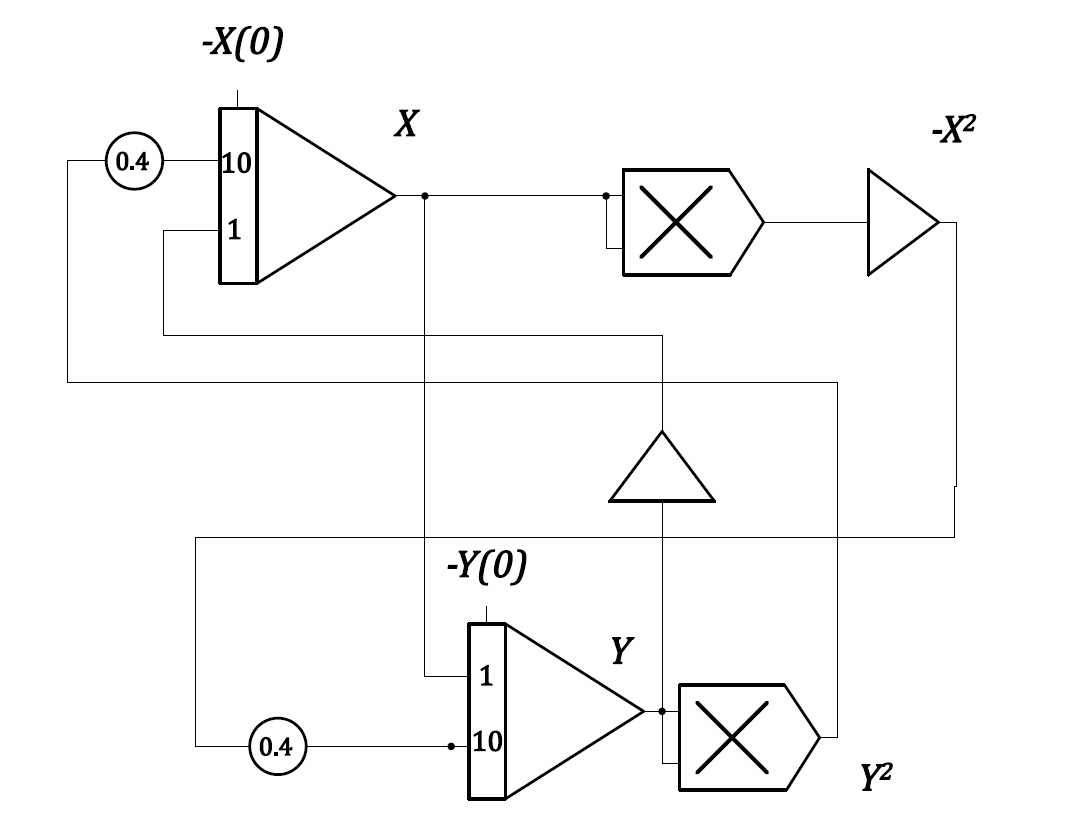
図 5 式(7)の演算回路
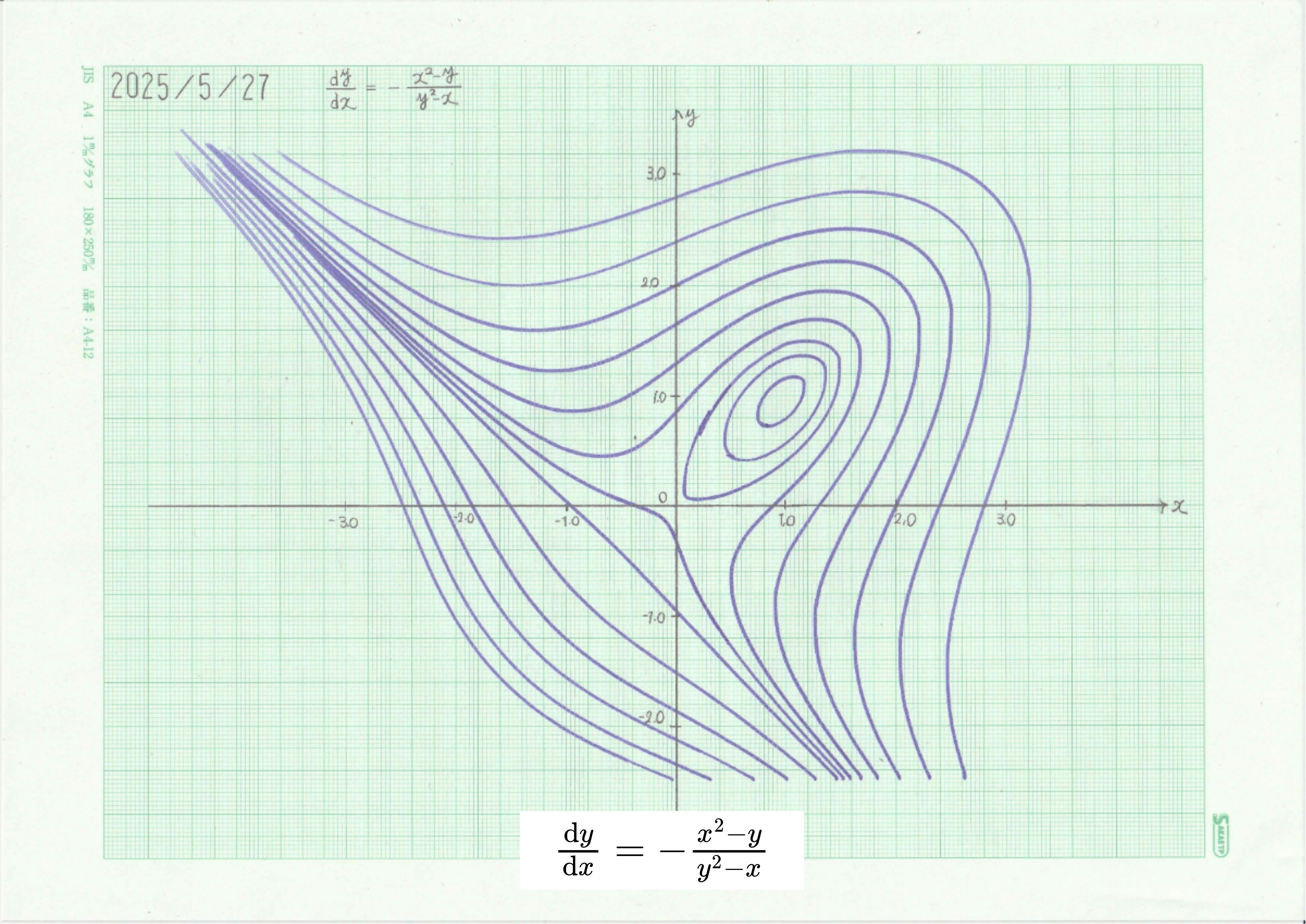
図 6 式(7)の積分曲線
原点及び \((x,y)=(1,1)\) が臨界点（平衡点）である。
系のヤコビ行列は
\[J=\begin{bmatrix}1&-2y\\-2x&-1\end{bmatrix}\tag{11}\]
と計算できる。\((0,0)\)での固有値は \(\pm1\) であり、これは正と負の実数であるから、鞍点である。\((1,1)\)での固有値は \(\pm\,\sqrt{3}i\) であり、互いに共役な純虚数であるので中心点（渦点）である。
図6からわかるように、初期条件によって周期解か発散解かが決定されるのだが、その境界線となる軌跡（セパラトリクス）は「デカルトの正葉線 (Folium of Descartes)」と呼ばれる代数曲線の一部である。
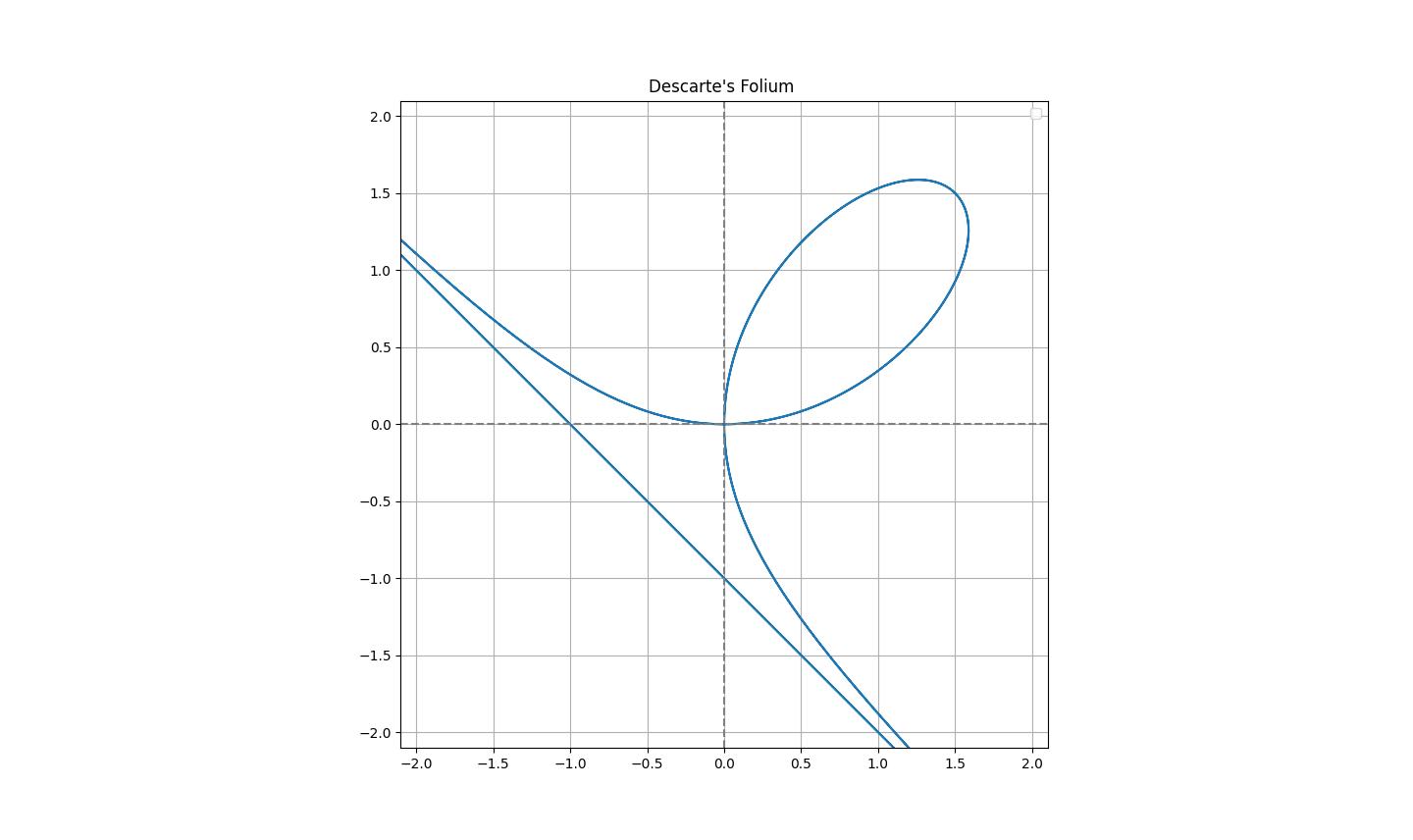
図 7 デカルトの正葉線
5.\(\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x^3-x}{y^3-y}\)
微分方程式
\[\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x^3-x}{y^3-y}\tag{12}\]
を解析する。
媒介変数\(t\)を導入すると、
\begin{cases}\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}&=x^3-x\\\\\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}&=-y^3+y\tag{13}\end{cases}
\(a_{X}=a_{Y}=1/2\) とすると、演算方程式は以下のようになる。
\begin{cases}\displaystyle{a_{\tau}}\frac{\mathrm{d}Y}{\mathrm{d}\tau}&=4X^3-X\\\\\displaystyle{a_{\tau}}\frac{\mathrm{d}X}{\mathrm{d}\tau}&=-4Y^3+Y\tag{14}\end{cases}
演算回路とアナログ計算機解を以下に示す。
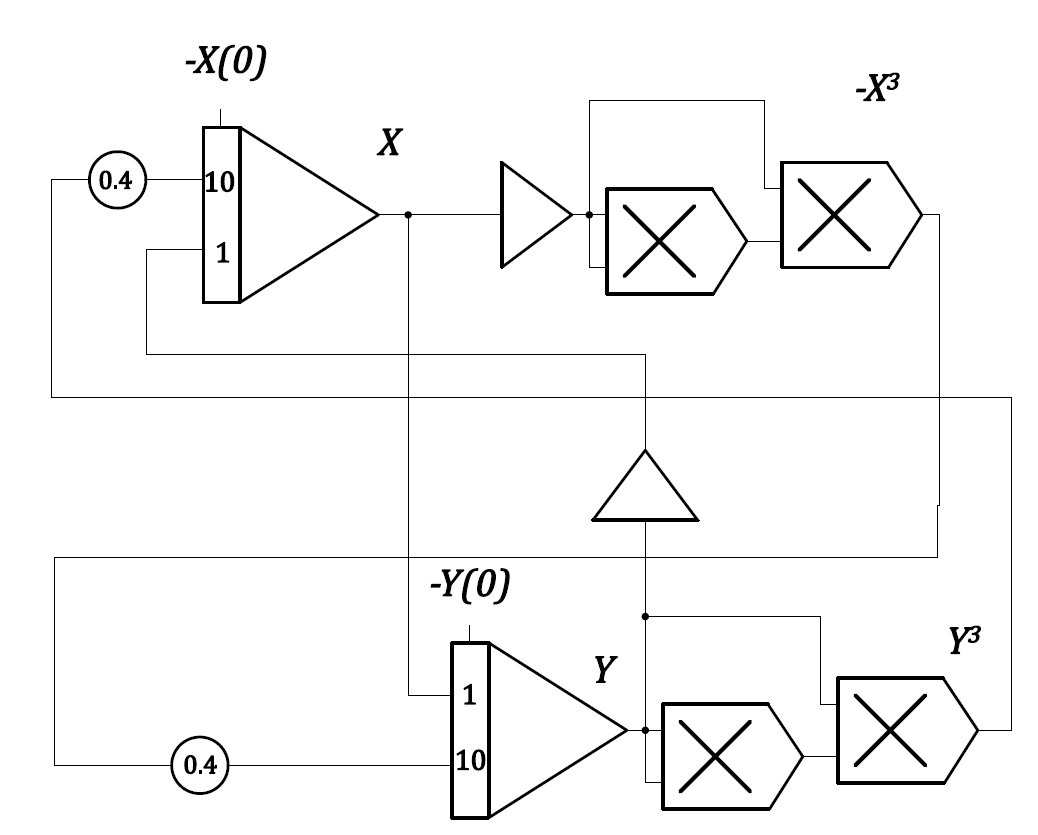
図 8 式(10)の演算回路
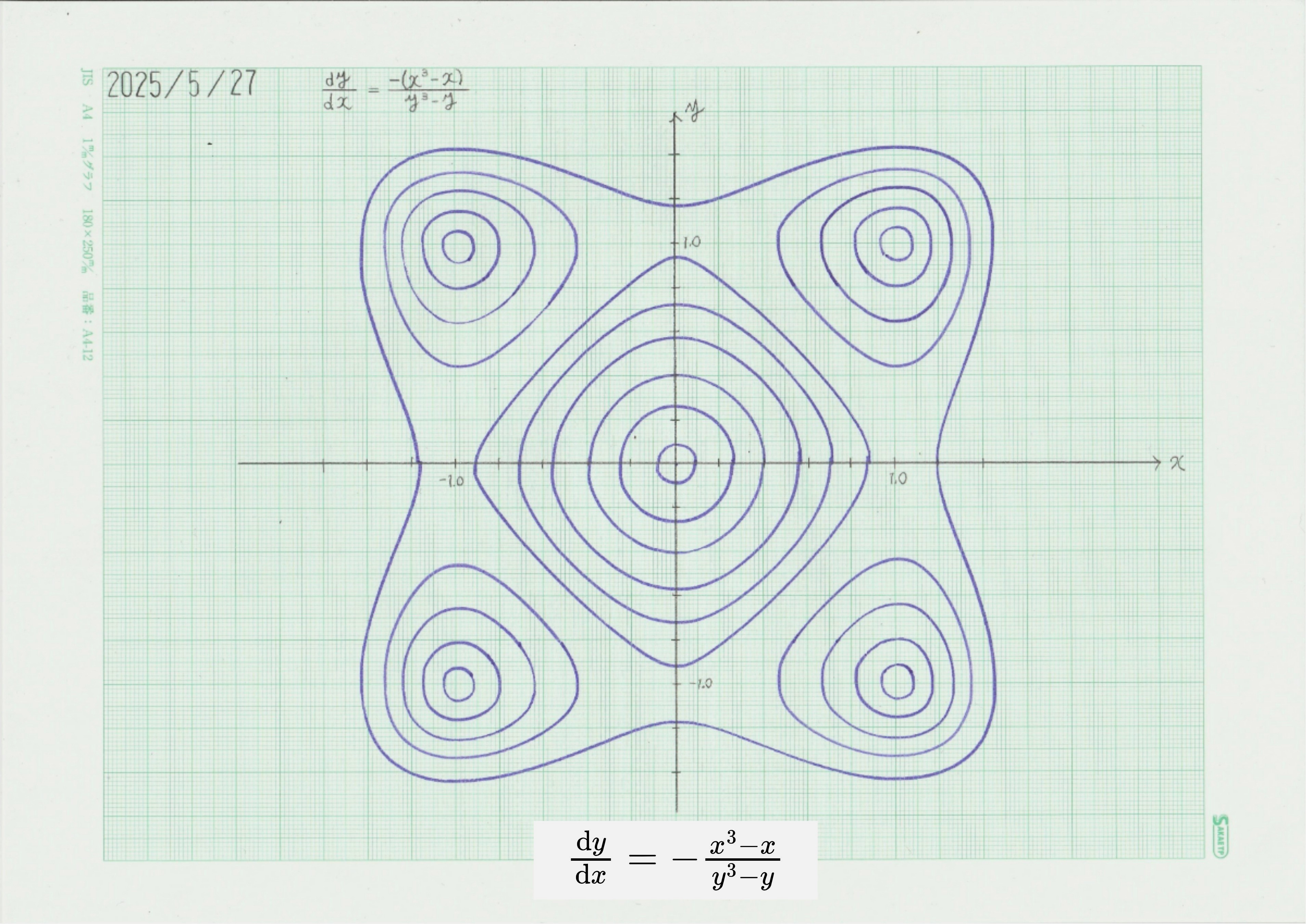
図 9 式(10)の積分曲線
臨界点は原点に加え、 \((-1,-1)\), \((-1,1)\), \((1,-1)\), \((1,1)\) 及び \((0,1)\), \((0,-1)\), \((-1,0)\), \((1,0)\) の計9か所である。系のヤコビ行列は
\[J=\begin{bmatrix}0&-3y^2+1\\3x^2-1x&0\end{bmatrix}\tag{15}\]
であり、計算すると、\(0,0\)および \((-1,-1)\), \((-1,1)\), \((1,-1)\), \((1,1)\)は中心点（渦点）で、\((0,1)\), \((0,-1)\), \((-1,0)\), \((1,0)\)は鞍点であることがわかる。
6.\(\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{-6y-x(3+x)}{y}\)
微分方程式
\[\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{-6y-x(3+x)}{y}\tag{16}\]
を解析する。これは、2階微分方程式
\[\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+0.6\frac{\mathrm{d}x}{\mathrm{d}t}+3x+x^2=0\tag{17}\]
の別表現である。2元1階連立微分方程式になおすと、
\begin{cases}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}&=&y\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}&=&-0.6y-3x-x^2=0\tag{18}\end{cases}
\(x\), \(y\) の電圧換算係数を\(1/10\)とすれば、演算方程式は
\begin{cases}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}&=&Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}&=&-0.6Y-3X-10X^2=0\tag{19}\end{cases}
となる。
アナログ計算機による演算解と、Pythonで計算した発散域・収束域の初期値マップを下に示す。
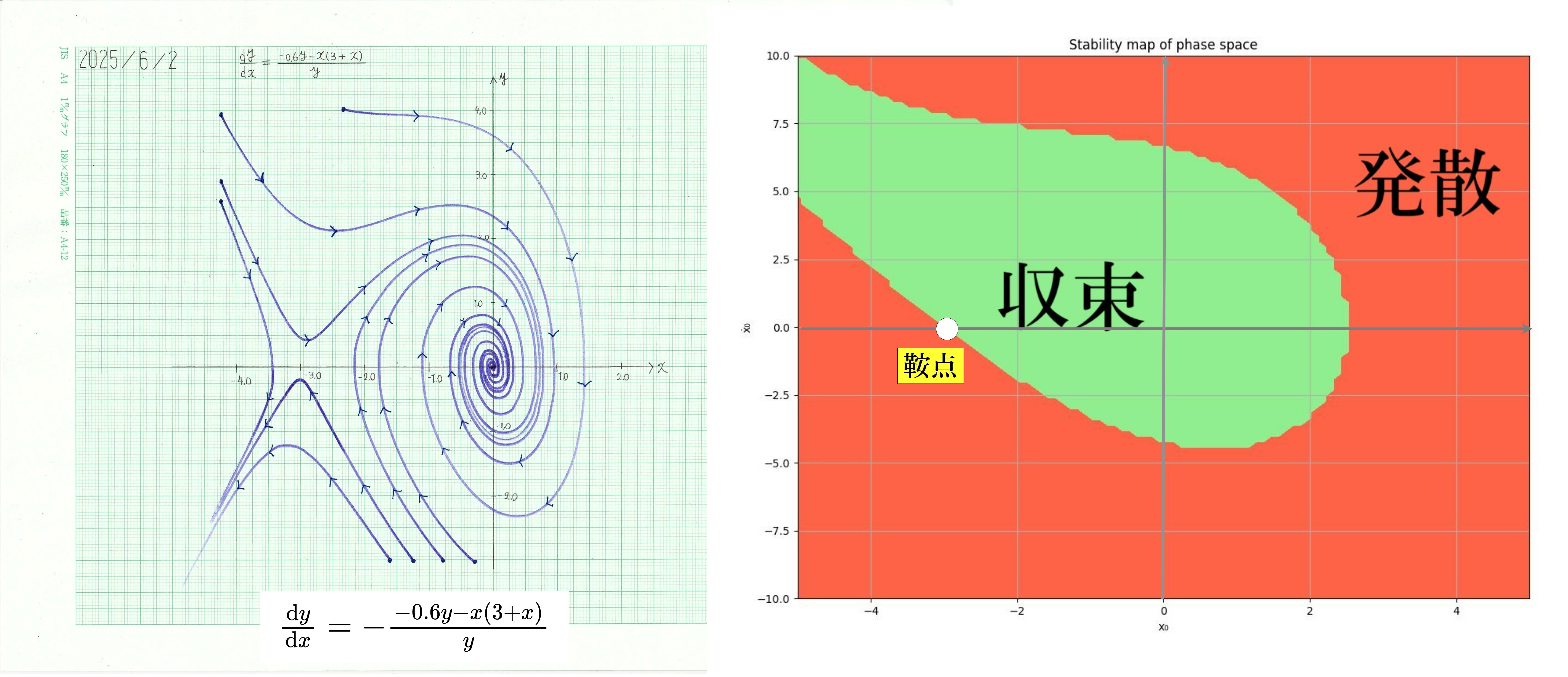
図 10 アナログ計算機で描画した積分曲線(左) / Pythonで描画した収束域・発散域のマップ(右)
\((-3,0)\) が鞍点、\((0,0)\) が安定焦点（渦状沈点）である。吸引域（basin of attraction）が第2象限遠方から原点まで伸びてきており、その領域内（緑）を通る積分曲線は \(t\rightarrow{\infty}\) で原点に収束する。逆に、セパラトリクスの外側領域(赤)を通る軌道は第3象限無限遠方へ発散する。
7.参考文献
[1] 西山 榮枝, 田辺 多知夫.「アナログ計算機によるdy/dx=P(x,y)/Q(x,y)の解析例とその誤差について」明治大学工学部研究報告, 1970, 第24巻, p.153-p.165