ルジャンドルの微分方程式
目次
1.準備
ベッセルの微分方程式に引き続き、ルジャンドルの微分方程式
\[(1-x^2)\,\frac{\mathrm{d}^2y(x)}{\mathrm{d}x^2}-2x\,\frac{\mathrm{d}y(x)}{\mathrm{d}x}+n\left(n+1\right)x\qquad{(n=0,1,2,\cdots)}\tag{1}\]
の\(\;0\lt{x}\lt{1}\)または\(\;-1\lt{x}\lt{1}\)の範囲における解(厳密には、基本解の1つである第1種ルジャンドル関数)をアナログコンピュータで得ることを考える。\(n\) が非負整数の場合、その解は多項式関数となる(ルジャンドル多項式 \(P_n(x)\))。
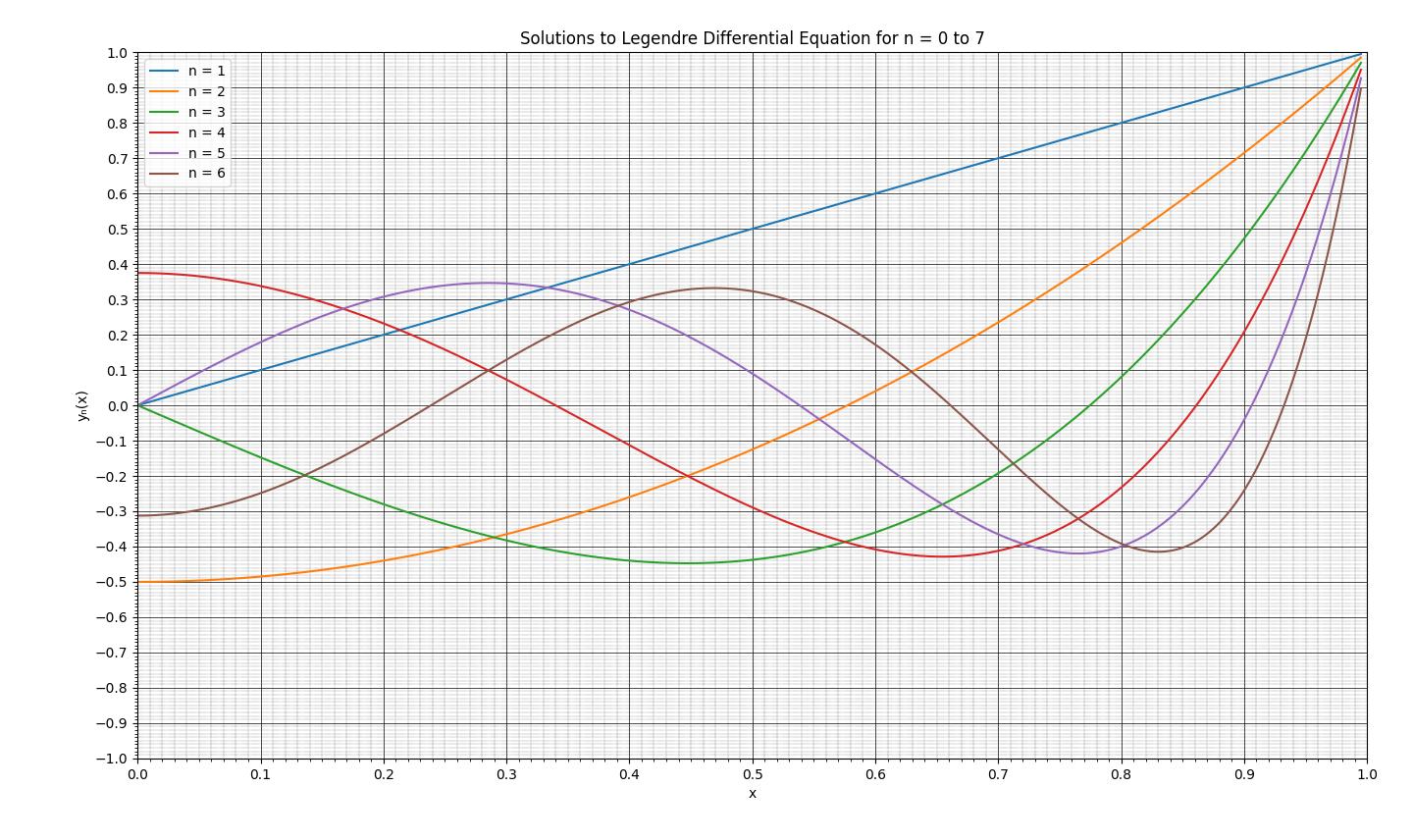
図1 ルジャンドル多項式 (\(n=1\)から\(n=6\)) の解
線形微分方程式であるものの、最高階の係数が変数であるから陽関数法では解けない。よって、陰関数法による実装を試みる必要がある。
2.アナログコンピュータプログラム
式(1)の演算する方法として、
- 通常の陰関数法による手法
- 媒介変数を利用する手法(Hausnerの方法)文献[1]
の2つが考えられる。後者についてはベッセルの微分方程式のアプリケーションページで適用例を示しているが、ほぼ同じ考え方である。
2.1 通常の陰関数法
本方式では、\(t\)の変域を[0,1]に制限するものとする。ルジャンドルの微分方程式の左辺を
\[(1-t^2)\frac{\mathrm{d}^2y}{\mathrm{d}t^2}-2\,t\,\frac{\mathrm{d}y}{\mathrm{d}t}+n(n+1)y=f(t)\tag{2}\]
とおく。いつものように定数\(a\)を用いた陰的表式
\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2}+\frac{f(t)}{a}=\frac{\mathrm{d}^2y}{\mathrm{d}t^2}\tag{3}\]
を定め、上式を実現する回路が安定する条件を求める。最高階に関する微係数
\[\frac{\mathrm{d}f(t)}{\mathrm{d}\frac{\mathrm{d}^2y}{\mathrm{d}t^2}}=1-t^2\tag{4}\]
は[0,1]において正を保つので、陰関数法回路の安定条件
\[\frac{1}{a}\frac{\mathrm{d}f(t)}{\mathrm{d}\frac{\mathrm{d}^2y}{\mathrm{d}t^2}}\lt{0}\tag{5}\]
を満たすためには
\[a\lt{0}\tag{6}\]
と定めればよいことがわかる。ここでは簡単のため\(a=-1\)としよう。方程式は、
\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2}-f(t)=\frac{\mathrm{d}^2y}{\mathrm{d}t^2}\tag{7}\]
すなわち
\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2}=t^2\,\frac{\mathrm{d}^2y}{\mathrm{d}t^2}+2\,t\,\frac{\mathrm{d}y}{\mathrm{d}t}-n(n+1)y\tag{8}\]
となる。
2.2 媒介変数法(Hausnerの方法)
微分方程式の独立変数を従属変数(媒介変数)にして、式中の特異点(極)を除去する方法である 。
独立変数を\(\,\theta\,\)とし、ルジャンドルの微分方程式
\[(1-\theta^2)\frac{\mathrm{d}^2x}{\mathrm{d}\theta^2}-2\,\theta\,\frac{\mathrm{d}x}{\mathrm{d}\theta}+n(n+1)x=0\tag{9}\]
を、2元1階の連立微分方程式に変換したのち、微分項について整理する。
\[\left\{\begin{array}{ll}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}\theta}=\displaystyle{y}\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}\theta}=\displaystyle\frac{2\,\theta\,y-n(n+1)x}{1-{\theta}^2}\end{array}\right.\tag{10}\]
\(\theta\)を媒介変数とみなして新独立変数\(\,t\,\)を導入し、(10)の両式に連鎖律を適用する。
\[\left\{\begin{array}{ll}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}=\displaystyle{y\,\frac{\mathrm{d}\theta}{\mathrm{d}t}}\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=\displaystyle\frac{2\,\theta\,y-n(n+1)x}{1-{\theta}^2}\frac{\mathrm{d}\theta}{\mathrm{d}t}\end{array}\right.\tag{11}\]
視察により、\[\frac{\mathrm{d}\theta}{\mathrm{d}t}=\xi(1-\theta^2)\qquad(\xi:定数)\tag{12}\]
となるように\(\theta\)を選べば方程式の極が消えることがわかる。\(\xi\)として1を選んだ場合、
\[\left\{\begin{array}{lll}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}=\displaystyle{(1-\theta^2)y}\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=\displaystyle{2\,\theta\,{y}-n(n+1)x}\\\\\displaystyle\frac{\mathrm{d}\theta}{\mathrm{d}t}=\displaystyle{1-\theta^2}\end{array}\right.\tag{13}\]
となる。\(\theta\)の初期条件として\(\theta(0)=0\)を定めれば、\(x(t)\)-\(\theta(t)\)グラフは[0,1]を変域とする解に、\(\theta(0)=-1\)を定めれば、[-1,1]を変域とする解が描かれる。
ちなみに、上記第3式(\(\theta\)についての微分方程式)の一般解は\[\theta=\mathrm{tanh}{(t+C)}\]である(Cは任意定数)。\(\theta\rightarrow{1}\;(t\rightarrow{\infty})\) であるから、XYレコーダなどで\(x(t)\)-\(\theta(t)\)グラフを描画するとき、\(\theta\) が1に近づくとペンの速度は次第に遅くなるはずである。
※ 文献[2]の57ページに同様の手法による演算回路の説明があるが、1階微分値が必要でない場合、上記における \((1-\theta^2)y\) を新たな変数として置いて乗算器を節約する便利な手法も紹介されている。興味のある方は文献をご参照ください。
2.3 演算方程式と演算回路
今回は、媒介変数法による演算法でグラフを求めることとする。
\(n=2,3,4,5,6\)の場合の解を求めるものとする。初期条件をうまく定めれば解関数\(x(\theta)\)は[-1,+1]の範囲に収まるので、\(x\)に関する電圧換算係数は一貫して\(a_{X}=1\)でよい。
一方、方程式から \(|\frac{\mathrm{d}x}{\mathrm{d}t}|\leq|\frac{\mathrm{d}x}{\mathrm{d}\theta}|\) がいえるので、スケーリングのボトルネックは明らかに\(\frac{\mathrm{d}x}{\mathrm{d}\theta}=Y\)である。ゆえに\(\frac{\mathrm{d}x}{\mathrm{d}\theta}=Y\)の電圧換算係数は\(\frac{\mathrm{d}x}{\mathrm{d}t}\) に関する電圧換算係数\(a_{\dot{X}}\)と共通とする。
\(n=7\)の\(|\frac{\mathrm{d}x}{\mathrm{d}\theta}|\)は変域端点で最大値\(28\)をとるので、\(a_{\dot{X}}=1/30\)を採るといいだろう。( 読み取り精度の向上の観点から、\(n\)の値に応じて\(\frac{\mathrm{d}x}{\mathrm{d}t}\)の換算係数を変えることが望ましい。)
\(\frac{\mathrm{d}y}{\mathrm{d}t}\)(元の式の2階微分項に相当)の電圧換算係数は \(\frac{\mathrm{d}x}{\mathrm{d}t}\)(元の式の1階微分に相当)の電圧換算係数と共通にしてよい。
以上から、演算方程式の一般形は
\[\left\{\begin{array}{lll}\displaystyle\frac{a_{\tau}}{a_{\dot{X}}}\frac{\mathrm{d}X}{\mathrm{d}\tau}=\displaystyle{\left(1-\frac{\Theta^2}{{a_{\Theta}}^2}\right)\frac{Y}{a_{\dot{X}}}}\\\\\displaystyle\frac{a_{\tau}}{a_{\dot{X}}}\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\displaystyle{2\frac{\Theta}{a_{\Theta}}\frac{Y}{a_{\dot{X}}}-n(n+1)\frac{X}{a_X}}\\\\\displaystyle\frac{a_{\tau}}{a_{\Theta}}\frac{\mathrm{d}\Theta}{\mathrm{d}\tau}=\displaystyle{1-\frac{\Theta^2}{{a_{\Theta}}^2}}\end{array}\right.\tag{14}\]
0.1Hz程度の低速演算でペンレコーダに結果を出力させる場合、いかなる\(n\)においても、\(a_{\tau}=10\,,a_{T}=1\,,a_{X}=1\,,a_{\Theta}=1\) は共通させることができる。係数設定の都合上、\(n=2,3,4\)のとき、\(a_{\dot{X}}=1/10\)とし、\(n=5,6\)のときは\(a_{\dot{X}}=1/30\)とする。
(1) \(n=2,3,4\)の場合の演算方程式
\[\left\{\begin{array}{lll}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=\displaystyle{\left(1-\Theta^2\right)\frac{Y}{10}}\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\displaystyle{\frac{2}{10}\,\Theta{Y}-\frac{n(n+1)}{100}X}\\\\\displaystyle{\frac{\mathrm{d}\Theta}{\mathrm{d}\tau}}=\displaystyle{\frac{1}{10}\left(1-\Theta^2\right)}\end{array}\right.\tag{15}\]
(2) \(n=5,6\)の場合の演算方程式
\[\left\{\begin{array}{lll}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=\displaystyle{\left(1-\Theta^2\right)\frac{Y}{10}}\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\displaystyle{\frac{2}{10}\,\Theta{Y}-\frac{n(n+1)}{300}X}\\\\\displaystyle{\frac{\mathrm{d}\Theta}{\mathrm{d}\tau}}=\displaystyle{\frac{1}{10}\left(1-\Theta^2\right)}\end{array}\right.\tag{15}\]
3.結果
低速演算の結果を示す。左が自作機による演算結果で、右は文献[2]の56ページに掲載されているグラフの抜粋であり、参考までに引用させていただいた。当たり前だが自作機の方が1960年代のものよりはるかに精度の良い解を得られる。
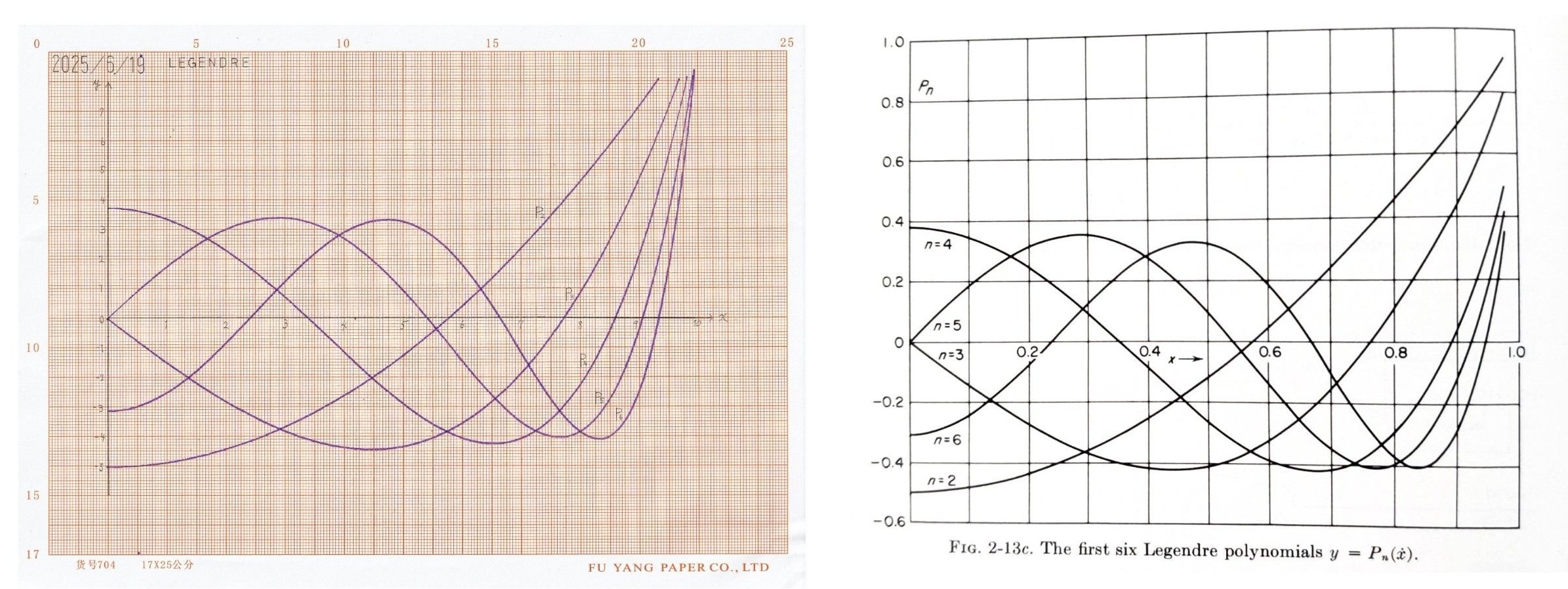
図2 ルジャンドル微分方程式のアナログ計算機解
4.参考文献
[1] A. Hausner, "Parametric Techniques for Eliminating Division and Treating Singularities in Computer Solutions of Ordinary Differential Equations," in IRE Transactions on Electronic Computers, vol. EC-11, no. 1, pp. 42-45, Feb. 1962.
[2] Granino A. korn & Theresa M. Korn. Electronic Analog And Hybrid Computers. McGraw-Hill Book Company, 1964.
[3] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」第1版, 岩波書店, 1975.