非線形インダクタンスを含む共振回路
目次
1.鉄共振回路
インダクタンスが電流に対して非線形に変化するコイルを用いた直列共振回路(図1.1)の動作を解析する。このような回路を鉄共振回路という。
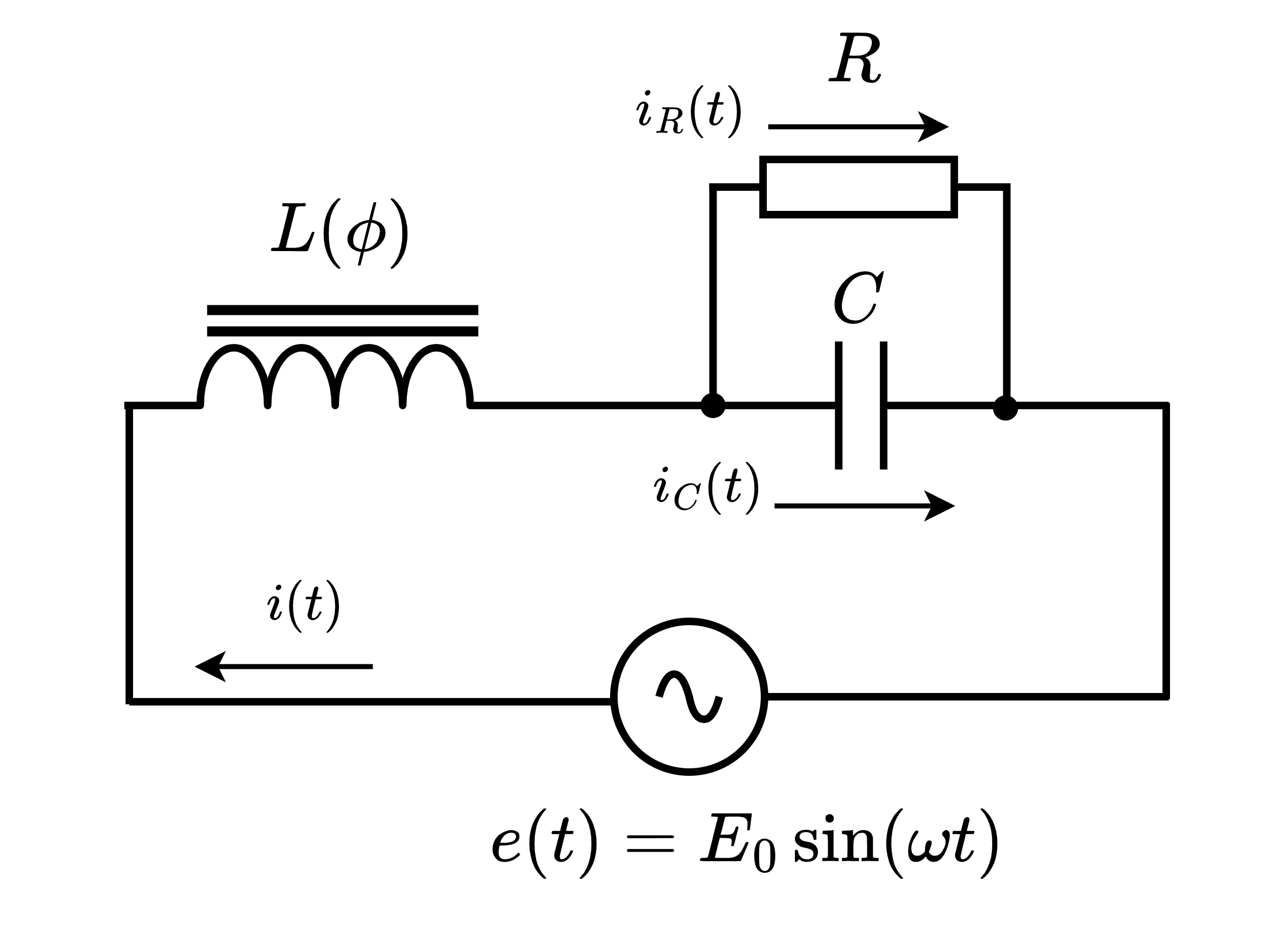
図 1
その回路方程式から導かれる無次元2階非線形常微分方程式系は京都大学の上田睆亮氏らによって研究され、相平面上での解軌道は「ウエダ・アトラクタ/ジャパニーズアトラクタ」と呼ばれる綺麗なストレンジアトラクタを生み出す。その研究にはデジタル計算機と併わせてアナログ計算機も使われたようだ。
(※ただし、上田氏はジャパニーズアトラクタに先立つ1961年に既にVan der Pol / Duffing混合型の微分方程式の研究でカオス現象を発見していた[2]。その際のストレンジアトラクタは「割れた卵アトラクタ」として知られている。)
コイルの巻き数を\(n\)、コイルを貫く磁束を\(\phi\)として回路方程式を立てると次のようになる。
\begin{eqnarray}n\frac{\mathrm{d}\phi}{\mathrm{d}t}+Ri_R&=&E\sin{\omega t}\tag{1}\\\\Ri_R&=&\frac{1}{C}\int{i_C}dt\tag{2}\\\\i&=&i_R+i_C\tag{3}\end{eqnarray}
コイルの電流-磁束特性はヒステリシスを無視して次の3次関数で表現できるとする。
\[i=a\,\phi^3\tag{4}\]
また、
\[n\omega^2C\phi_n=a\,\phi_n^3\tag{5}\]
となるように正規化係数\(\phi_n\)を定めて磁束\(\phi\)を無次元化する。
\[\phi/\phi_n=x\tag{6}\]
以上をもとに\(x\)についての微分方程式を導くと
\[\frac{\mathrm{d}^2x}{\mathrm{d}\tau^2}+k\frac{\mathrm{d}x}{\mathrm{d}\tau}+x^3=B\cos{\tau}\tag{7}\]
ただし \(\tau=\omega t-\arctan{k},\; k=1/{\omega CR},\,B=E\sqrt{1+k^2}/{n\omega\phi_n}\)
(7)式はDuffing方程式
\[\ddot{x}+\delta\dot{x}+\alpha x+\beta x^3=\gamma \cos{\omega t}\tag{8}\]
の特別な形であり、線形減衰項+非線形(3次)復元項+周期強制項を有する2階微分方程式である。
上田氏の論文[1]ではパラメータが\((k,B)=(0.1,12.0)\)のとき,文献[5]は\((0.05, 7.5)\)のとき生じる不規則振動(ストレンジアトラクタ)を取り扱っている。我々前者の係数を採用する。
2.アナログコンピュータプログラム
2.1 演算方程式
もとの方程式は
\begin{array}{l}\displaystyle\frac{\mathrm{d}^2x}{\mathrm{d}t^2}&=&-k \,\frac{\mathrm{d}x}{\mathrm{d}t}-x^3+B\cos{t}\tag{9}\end{array}
であるが、スケーリングのため、これを2元の1階連立微分方程式に直すと
\begin{array}{ll}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}=y\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=\displaystyle{-k y-x^3+B\cos{t}}\tag{10}\end{array}
となる。\(k=0.5\,,B=12\)のとき、\(|x|\)の最大値は3.5程度、\(|y|\)の最大値は9弱なので、それぞれの電圧換算係数は \(a_{X}=1/4\)、\(a_{Y}=1/10\)と定めればよいだろう。強制力については\(f(t)\) と置き直し、換算係数を\(a_{F}=1/12\)とする。時間換算係数をひとまず\(a_{\tau}=1\)とおき、演算方程式に直す。
\begin{array}{ll}\displaystyle\frac{a_{\tau}}{a_{X}}\frac{\mathrm{d}X}{\mathrm{d}\tau}=\displaystyle\frac{Y}{a_{Y}}\\\\\displaystyle\frac{a_{\tau}}{a_{Y}}\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\displaystyle{-0.1 \frac{Y}{a_{Y}}-\frac{X^3}{{a_{X}}^3}+\frac{F(\tau)}{a_{F}}}\tag{11}\end{array}
各値を代入して整理すれば
\begin{array}{ll}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=2.5Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=-0.1\,Y-6.4 X^3+1.2F(\tau)\tag{12}\end{array}
よって(11)式をもとにプログラムを組めばよい。
2.2 ブロックダイヤグラム
演算回路は以下の如く結線される。
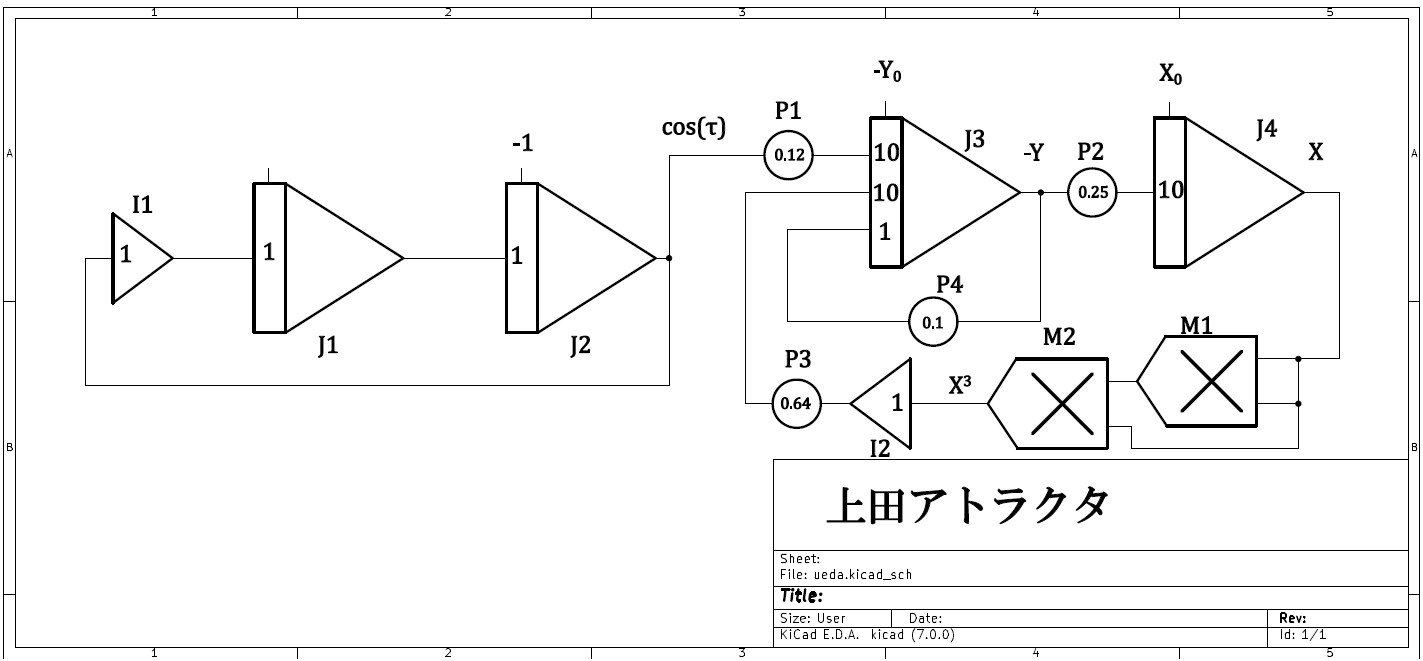
図2 ブロックダイヤグラム
3.結果
高速モードにおける演算結果を図3に示す。
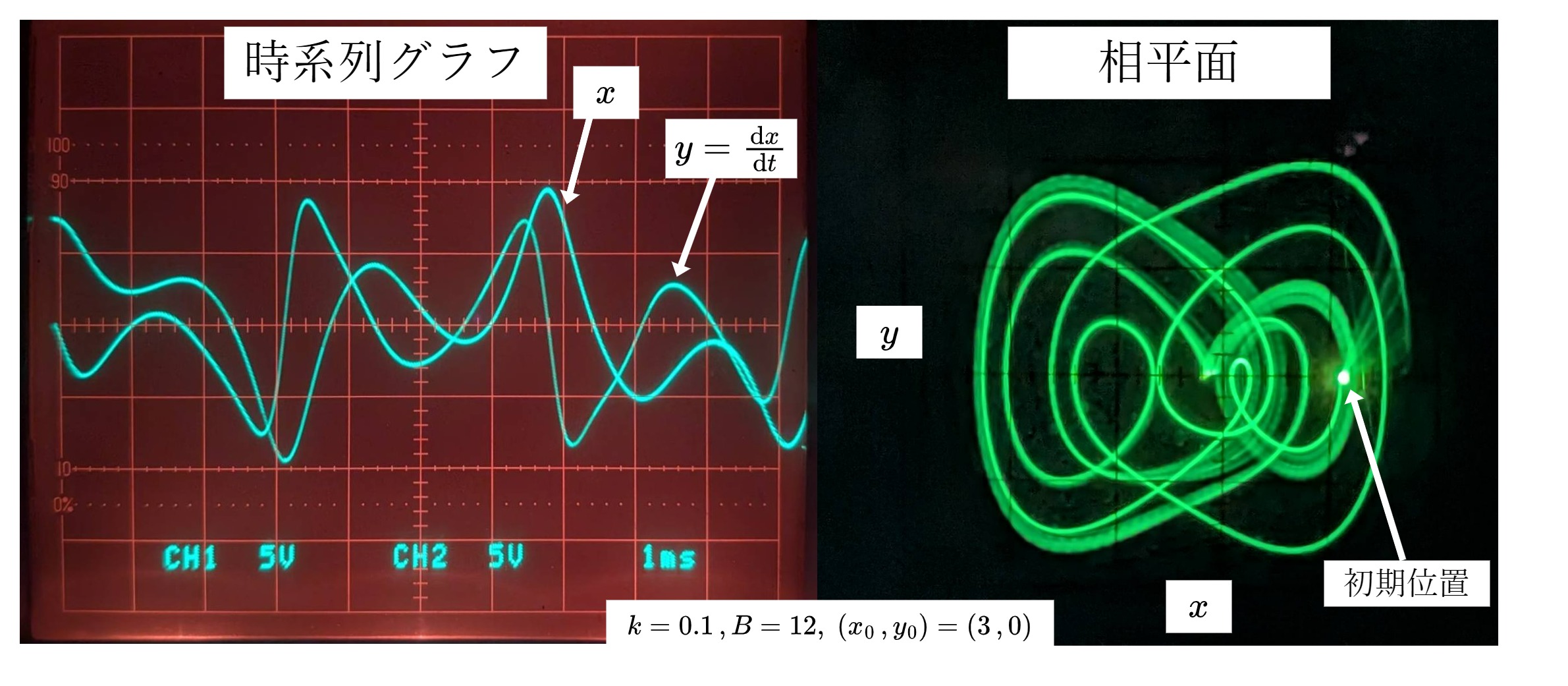
図3 高速モードにおける解
低速モードでアナログコンピュータを駆動し、グラフをXYレコーダに描かせたものが図4である。図5の数値解(Scipyのodeintモジュールによる)と比較していただきたい。
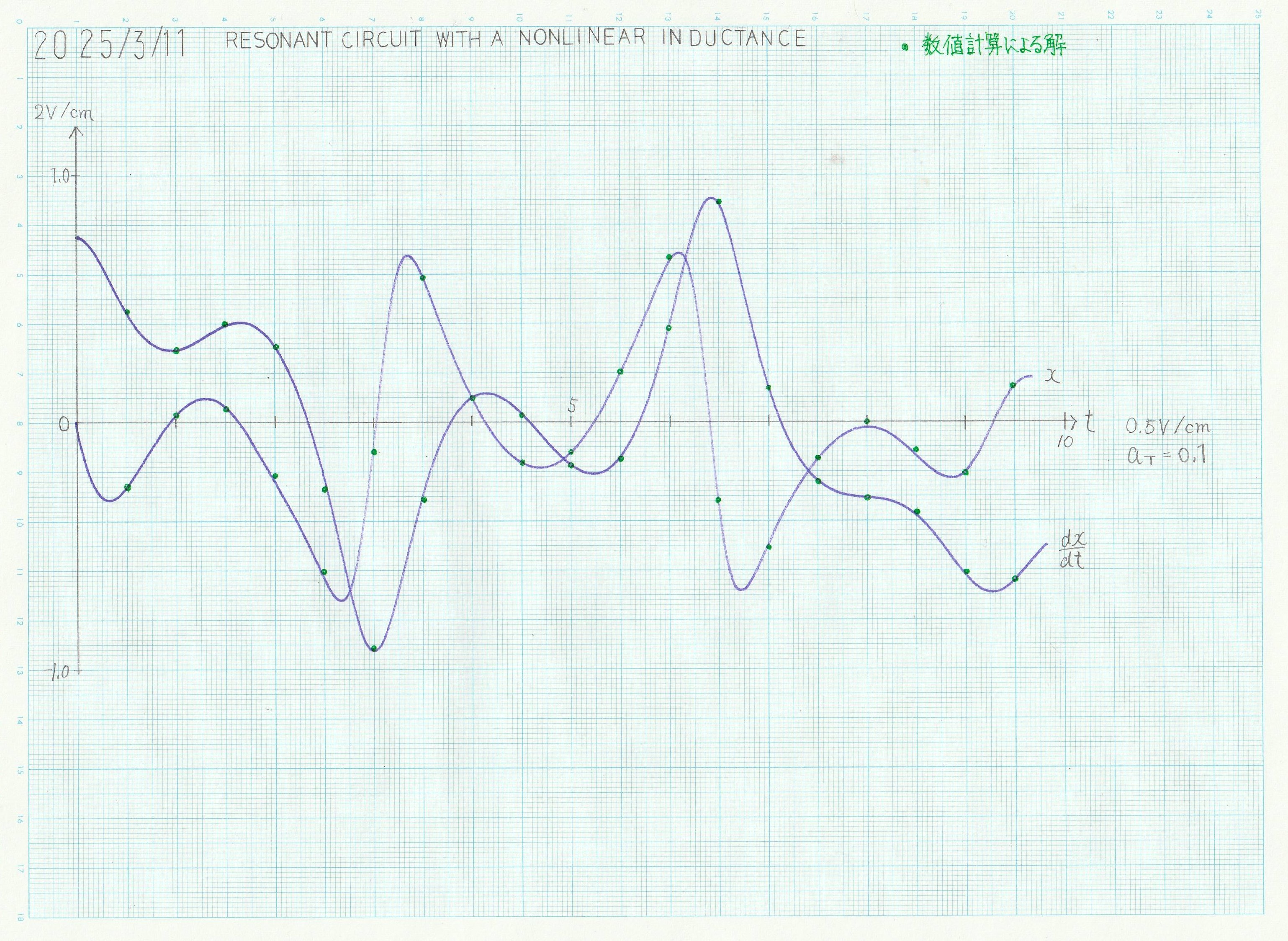
図4 低速モードにおける解
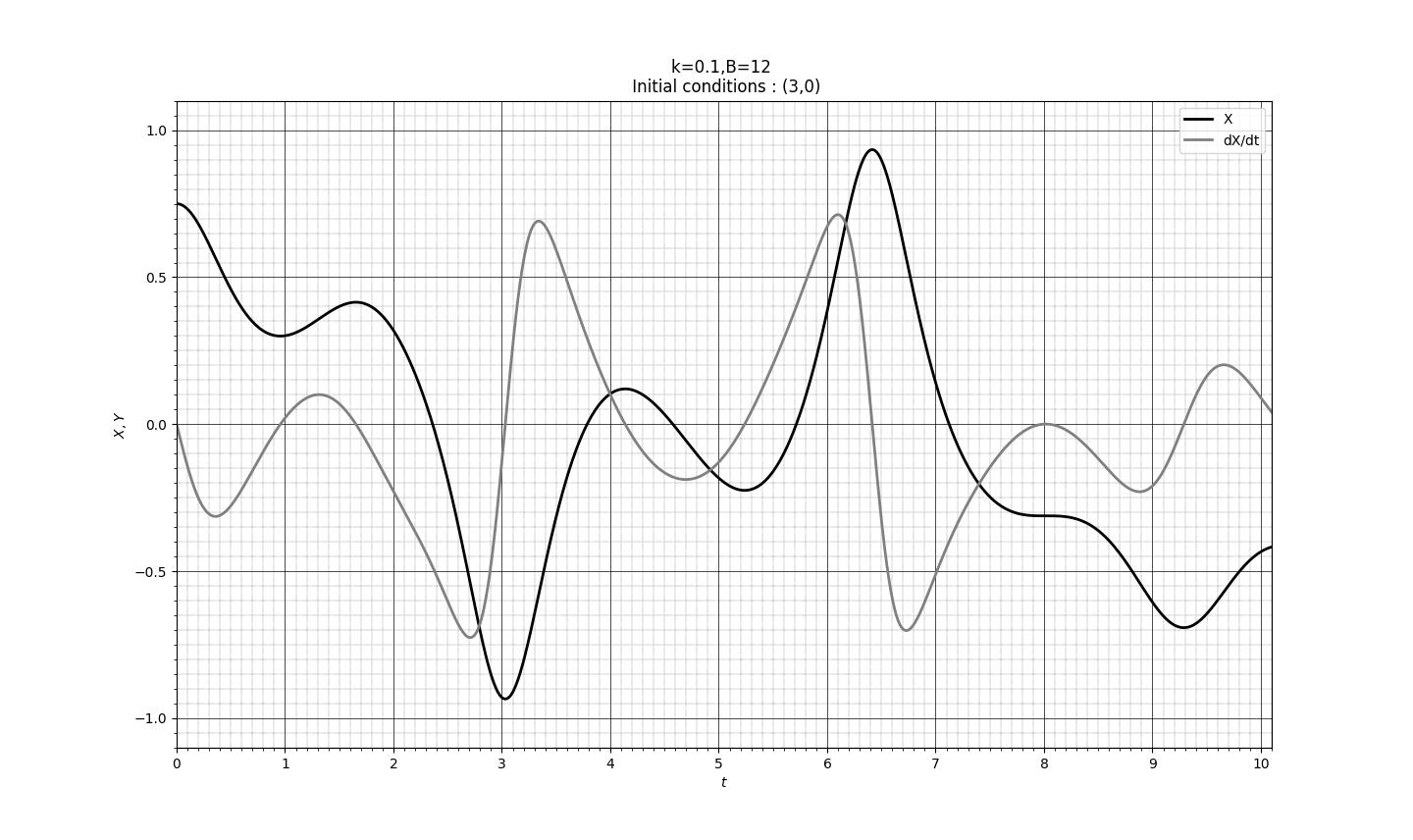
図5 数値計算の結果
低速モードにおいては、数値計算の結果とアナログコンピュータによる解はきわめて良く一致している。一方の高速モードでは時間が経つにつれ誤差が目立っているが、\(t\)が小さい領域では十分正確な解が得られている。
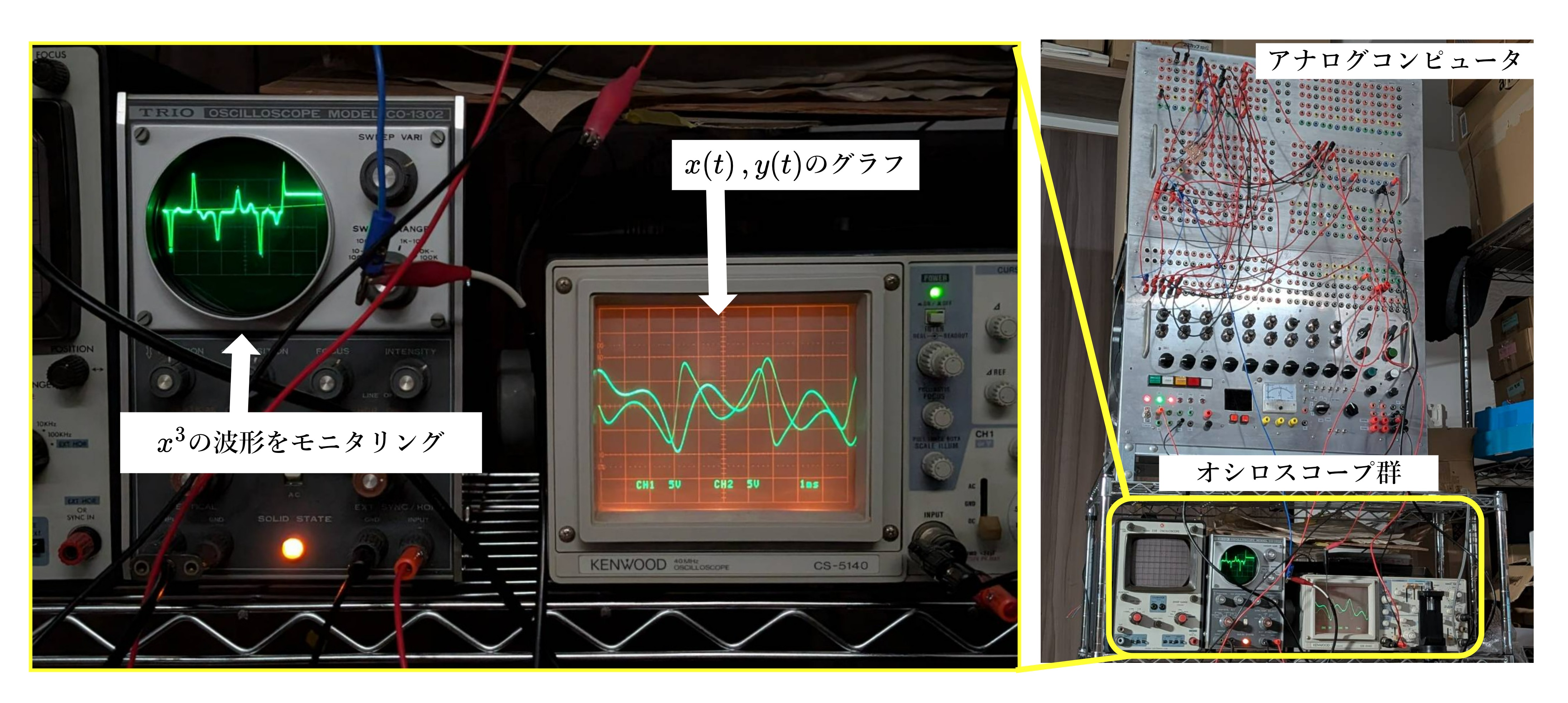
図6 アナログコンピュータ運用の様子
参考までに、\((k,B)=(0.1,12.0),(0.05,7.5)\)のときの数値計算結果を併せて示しておく。
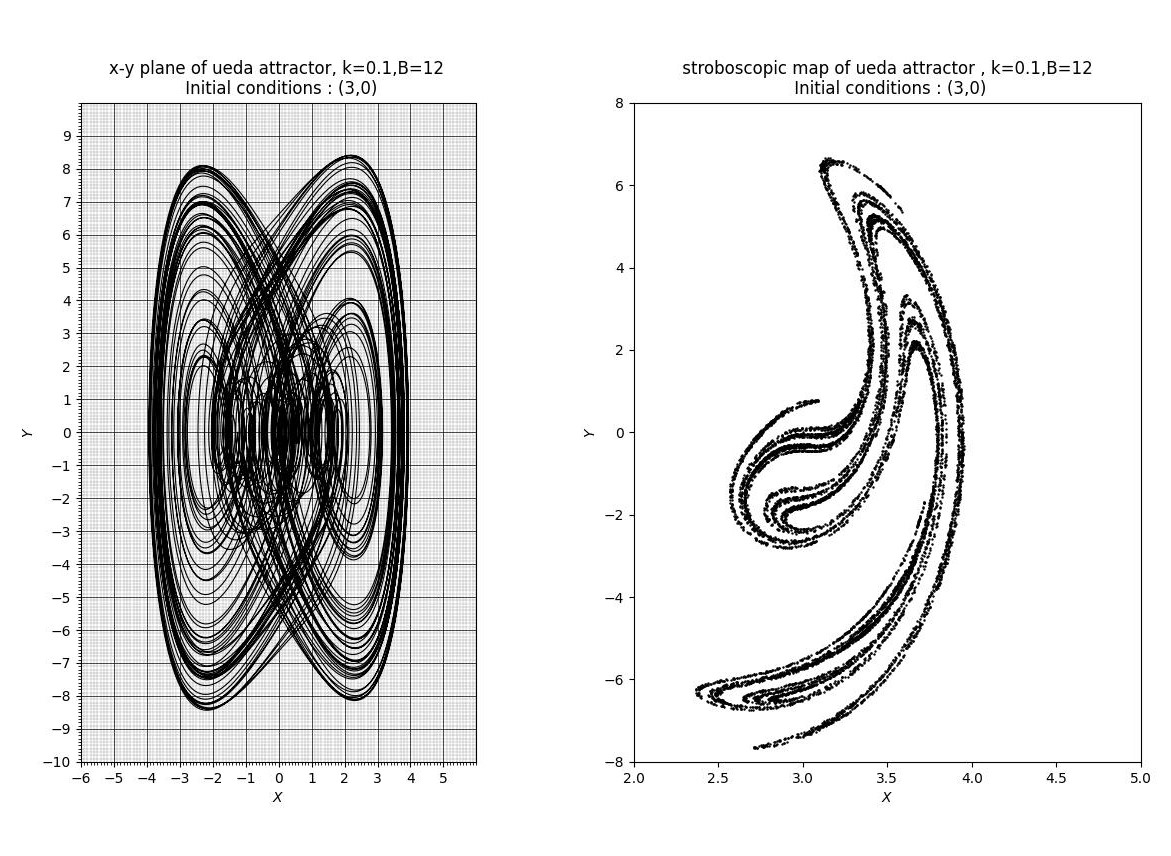
図7
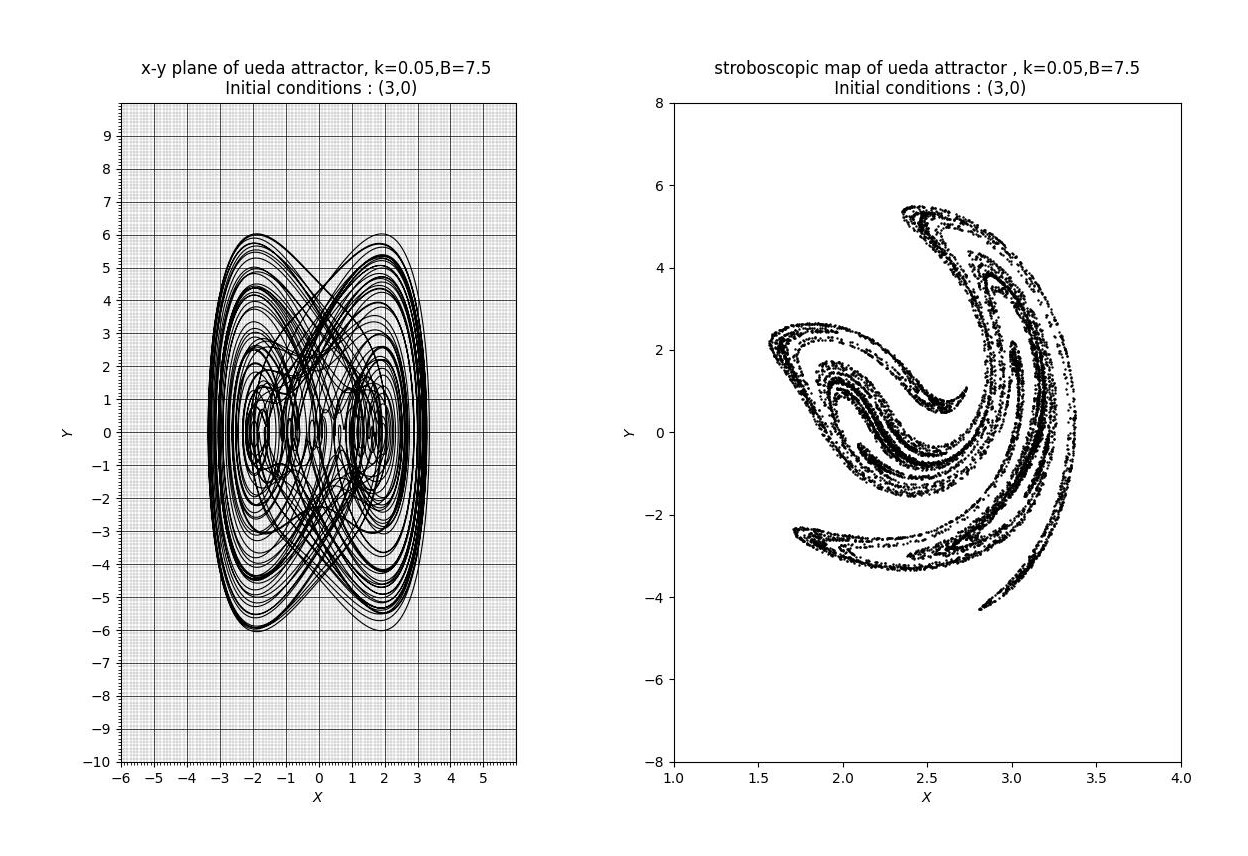
図8
左側はx-y相平面図であり、右側は強制項の位相が\(2\pi\)になるごとに(\(\tau\)が\(2\pi\)の整数倍になるごとに)プロットしたストロボ写像である。文献[1]の第3図とほぼ同じ画像が得られた。ストロボ写像の方は軸のスケールが異なることに注意されたい。
4.参考文献
[1]上田睆亮. 「非線形性に基づく確率統計現象-Duffing方程式で表わされる系の場合-」電気学会論文誌A ,98巻3号, pp47-53, 1978.
[2]上田睆亮. 「周波数引込・抑制現象のはざ間に現れた謎の正体 ーNLP 報告書の数値が全てを語っているー」 電子情報通信学会 基礎・境界ソサイエティ Fundamentals Review,7巻 3号, pp172-185, 2014. https://www.jstage.jst.go.jp/article/essfr/7/3/7_172/_pdf/-char/ja
[3]大嶋健司. 「可飽和鉄心を持つ電気回路に発生する非線形振動」電気学会論文誌 A, 95巻 11号, pp 475-482,1975. https://www.jstage.jst.go.jp/article/ieejfms1972/95/11/95_11_475/_pdf/-char/en
[4] 中川孝之.「鉄共振現象についての考察」富山大学工学部紀要 6巻, 1/2号, p.1-3,1955.
[5] Kyoto-U OCW 『京都大学1999年度最終講義 上田 睆亮(工学研究科教授)「カオス研究の経緯と将来展望」2000年3月3日』YouTubeリンク ←上田氏ご本人の講演。途中で割れた卵アトラクタについての説明がある。研究に使われたであろうアナログコンピュータの写真も確認できる。
[6] Dumitru Deleanu. 「Description of strange attractors using invariants of phase-plane」 https://www.researchgate.net/publication/228521797_Description_of_strange_attractors_using_invariants_of_phase-plane