ファンデルポール方程式
目次
1.ファンデルポール方程式
\(\mu\)を正のパラメータとしたとき、2階非線形微分方程式
\[\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\mu\,(x^2-1)\frac{\mathrm{d}x}{\mathrm{d}t}+x=0\tag{1}\]
は十分大きな \(t\) で周期振動解(自励振動)を持ち、式(1)はファンデルポール方程式 ( Van der Pol equation )と呼ばれるもので、非線形力学などでよく題材にされる、解析的に解けない微分方程式の1つである。もとは真空管を用いた自励発振回路の挙動の研究で定式化されたものであるが、フルードの振子 (Floude's pendulum)のような力学系でも現れる。
最大の特徴として、独立変数が無限大に向かうとき、相平面上の解軌道がある閉軌道に収束することが挙げられる。その閉軌道を極限軌道(リミットサイクル)という。
2.アナログコンピュータプログラム
1階連立系に直すと、
\begin{cases}\displaystyle{\frac{\mathrm{d}x}{\mathrm{d}t}}=y\\\\\displaystyle{\frac{\mathrm{d}y}{\mathrm{d}t}}=\mu\,(1-x^2)y-x\tag{2}\end{cases}
\(a_X,\,a_Y\) として1/3を選ぶと、演算方程式は次のようになる。
\begin{cases}\displaystyle{a_{\tau}\frac{\mathrm{d}X}{\mathrm{d}\tau}}=Y\\\\\displaystyle{a_{\tau}\frac{\mathrm{d}Y}{\mathrm{d}\tau}}=9\,\mu\,\left(\frac{1}{9}-X^2\right)Y-X\tag{3}\end{cases}
\(\mu\)が1以下のときのブロックダイヤグラムは下図の通り。積分器には適宜初期条件を与えればいいが、自励振動系であるから、原点を初期値としても振動解は得られる。
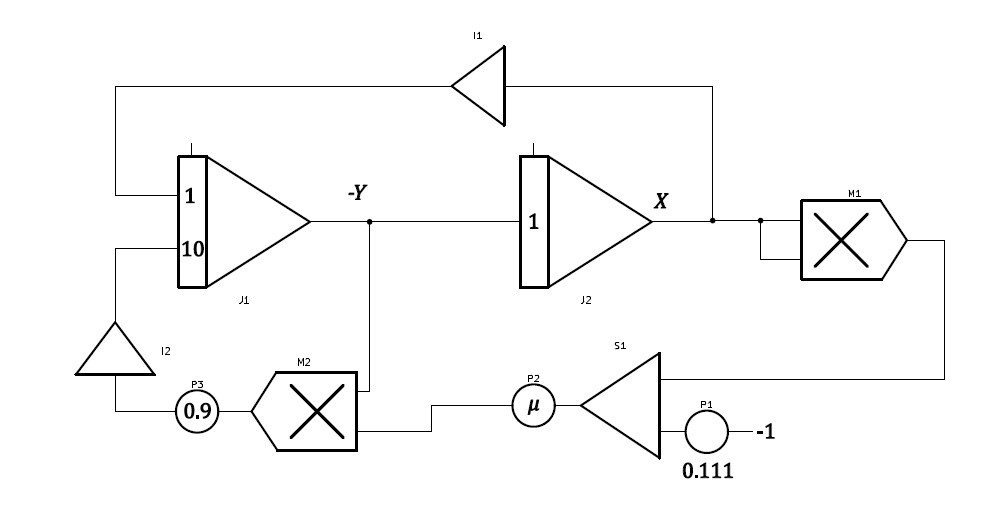
3.結果
時間換算係数 \(a_{\tau}\) を1として、低速モードで演算してXYレコーダで記録した結果を次の図に示す。
\(\mu\) の値が小さければ小さい程、その極限軌道は円に近づく(つまり解波形の形状が正弦波に近づく)。\(\mu\) が大きいと極限軌道はより"ひしゃげた"形となり、解波形は特徴的な振動波形(弛緩振動 relaxation oscillationと呼ばれる)になる。
原点 \((x,y)=(0,0)\) はこの系の唯一の平衡点で、不安定焦点であり、その近傍から出発する軌道は極限軌道に漸近する。極限軌道の外側に初期点を与えると、こちらも位相平面上で極限軌道に巻き付くように漸近する。また、\(\mu\) の値によって極限軌道へ内側から収束するのにかかる時間も大きく異なっていることがわかる。
次に等傾斜線を描きだすことも試みた。等傾斜線とは、相平面上で軌道の傾き \(\mathrm{d}y/\mathrm{d}x\) が等しい点を結んだ曲線を指し、傾きをパラメータとして代数的に表式が得られる。そのため、電子計算機出現以前は微分方程式の図的方法としてこの等傾斜線をプロットして解軌道を追跡する方法(等傾斜法)が用いられることがあった。
ファンデルポール方程式の場合、前述の \(y\),\(x\) を用いた表現を1つの式として表すと
\[\frac{\mathrm{d}y}{\mathrm{d}t}=\mu\,(1-x^2)-x\tag{4}\]
連鎖律を適用して、
\begin{eqnarray}\frac{\mathrm{d}y}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t}&=&\mu\,(1-x^2)-x\\\\\frac{\mathrm{d}y}{\mathrm{d}x}\,y&=&\mu\,(1-x^2)-x\tag{5}\end{eqnarray}
軌道の傾き \(\mathrm{d}y/\mathrm{d}x\) をパラメータ \(m\) とおいて整理すると、
\[y=\frac{x}{\mu\,(1-x^2)-m}\tag{6}\]
(6)式の\(x\)を独立変数として、さまざまな \(m\) の値でXYレコーダ上にプロットすればよい。アナログコンピュータの演算回路としては割算器が必要になる。最急降下法を用いた除算法では原点付近で誤差が出たので、仕方なしに2象限割算器(通常のアナログ除算法)を用いることとし、分母の符号が変わるごとに回路を組みなおして運用した。回路組み直しのことを考えると、(6)式の独立変数は積分器による自動掃引ではなく、ポテンショメータでの手動掃引の方がよいだろう。もちろんスケーリングも忘れずに行うこと。分母分子のいずれかが1MUを超過する場合は、両方を同じ数で除したものを割算回路に入力するのがセオリーである。今回は、\(a_{X}=1/3\)かつ \(a_{Y}=1/3\) であるから、(6)の演算方程式は
\begin{eqnarray}\frac{Y}{a_{Y}}&=&\frac{\frac{X}{a_{X}}}{\mu\,(1-\frac{X^2}{{a_{X}}^2})-m}\\\\&=&\frac{X}{\mu(1-9X^2)-m}\tag{7}\end{eqnarray}
スケーリングのため分母と分子を10で割って
\[Y=\frac{0.1X}{\mu\,(0.1-0.9X^2)-m/10}\tag{8}\]
と求まる。
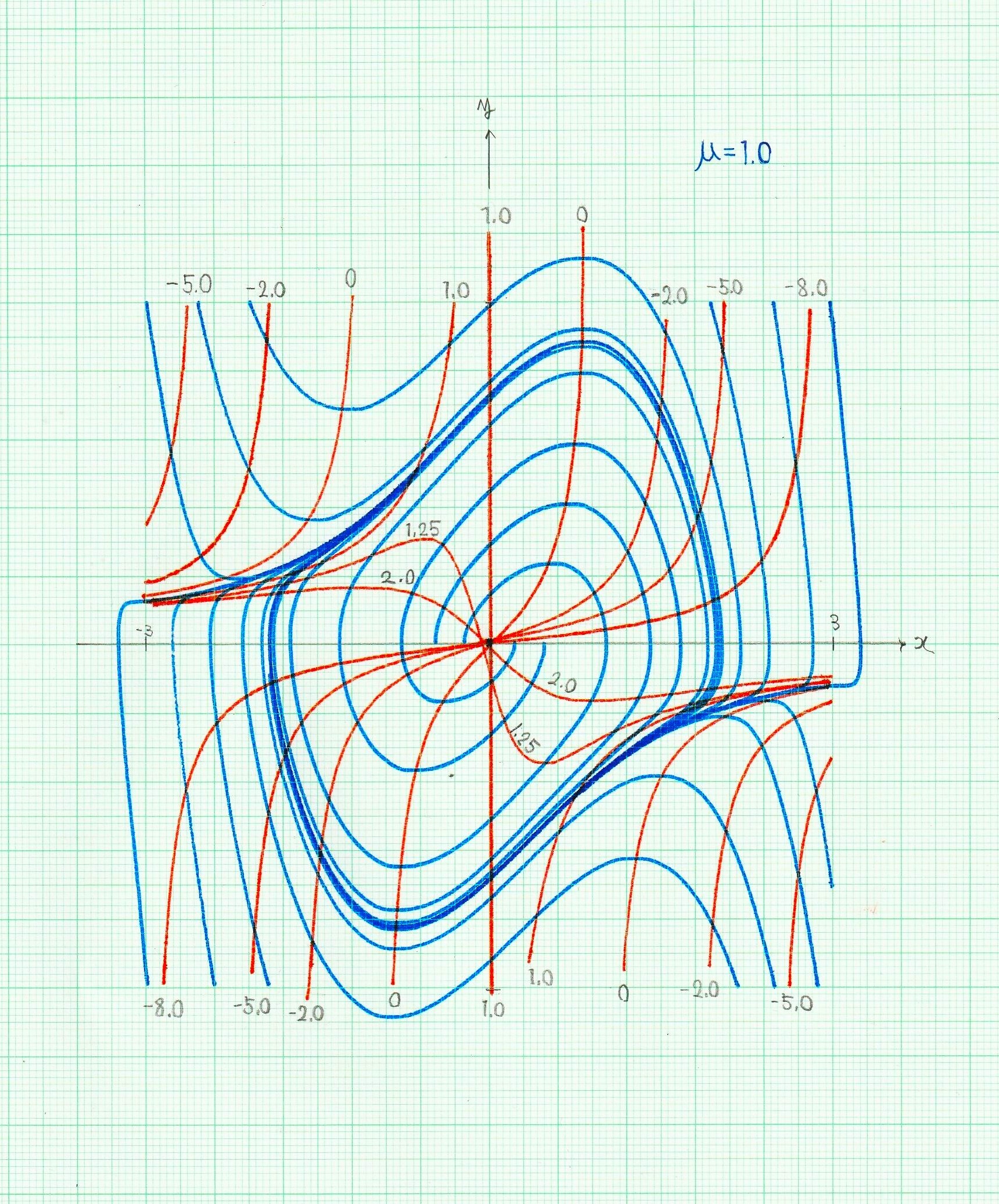
\(\mu=1.0\) として、相平面上で解軌道と等傾斜線をプロットした図を以下に示す。特異点である原点以外では、位相面上での軌道の傾きが一義的に定まることが分かる。
4.参考文献
[1] 有山 正孝. 「基礎物理学選書 8. 振動・波動」第37版, 裳華房, 2008.
[2] 奥田 恵孝. 「非線形常微分方程式の実際的解法」北海道学芸大学紀要(第二部), 7巻,1号, p17-p33, 1956.