送電系統における開閉サージの過渡解析
目次
1.モデル化・回路方程式
母線側に直列リアクトルのない送電系統でコンデンサを開閉した時、母線側に発生する過渡電圧は小さいが、変圧器の低圧側に高い過渡電圧が発生することがある。この現象をアナログコンピュータで解析する。(文献[1]の7.3節 p.151-p.155に掲載されている題材である。)
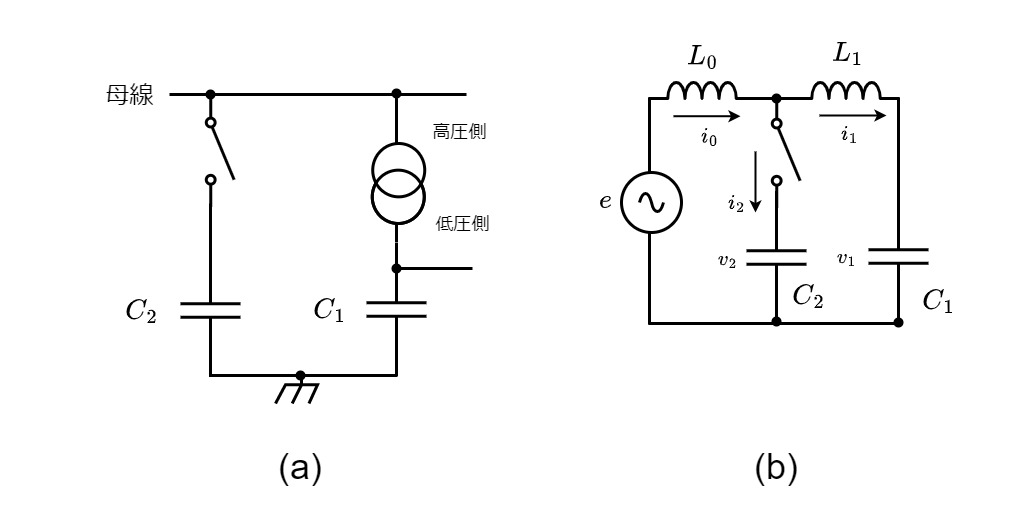
図1
図1.1(a)に示す送電系統を等価回路で表現した(b)が今回の解析対象である。\(L_0\)は経路短絡インダクタンス、\(L_1\)は変圧器の漏れインダクタンスを含む線路インダクタンス、\(C_1\)は低圧側の総キャパシタンスであり、Sは開閉器を示す。Sを投入しコンデンサ\(C_2\)を系統に接続した後の回路方程式は以下のようになる。
\begin{eqnarray}e-v_2&=&L_0\frac{\mathrm{d}i_0}{\mathrm{d}t}\tag{1}\\\\v_2-v_1&=&L_1\frac{\mathrm{d}i_1}{\mathrm{d}t}\tag{2}\\\\C_2\frac{\mathrm{d}v_2}{\mathrm{d}t}&=&i_2\tag{3}\\\\C_1\frac{\mathrm{d}v_1}{\mathrm{d}t}&=&i_1\tag{4}\\\\i_0&=&i_1+i_2\tag{5}\end{eqnarray}
2.アナログコンピュータプログラム
2.1 演算方程式
送電系統の定格線間電圧として22kVを想定する。\(e=E\cos{(\omega t)}\)とおくと、\(E=22000\frac{\sqrt{2}}{\sqrt{3}}\) kVとなる。電源の角周波数は\(\omega=2\pi\times 60\) rad/sとし、\(\omega L_0 =1\) Ω、\(1/{\omega C_2}=100\) Ωとする。さらに、静電容量やインダクタンスの比 \(m\equiv\frac{C_2}{C_1}, n\equiv\frac{L_0}{L_1}\)を定め、回路方程式を書き直せば
\begin{eqnarray}e-v_2&=&\frac{1}{120\pi}\frac{\mathrm{d}i_0}{\mathrm{d}t}\tag{6}\\\\v_2-v_1&=&\frac{1}{120\,n\,\pi}\frac{\mathrm{d}i_1}{\mathrm{d}t}\tag{7}\\\\\frac{1}{1.2\times 10^{4}\pi}\frac{\mathrm{d}v_2}{\mathrm{d}t}&=&i_2\tag{8}\\\\\frac{1}{1.2\times 10^{4}\,m\,\pi}\frac{\mathrm{d}v_1}{\mathrm{d}t}&=&i_1\tag{9}\\\\i_0&=&i_1+i_2\tag{10}\end{eqnarray}
と原方程式が整理される。低速実時間演算を想定し、時間換算係数を\(a_\tau = \omega = 120\pi \)、電圧換算係数を\(a_V=\frac{0.1}{22000\sqrt{2}/\sqrt{3}},\quad a_I = \frac{1}{22000\sqrt{2}/\sqrt{3}}\)とすると、演算方程式は次のようになる。
\begin{eqnarray}22000\frac{\sqrt{2}}{\sqrt{3}}\cos{\left(\frac{120\pi}{120\pi}\tau\right)}-\frac{220000\sqrt{2}}{\sqrt{3}}V_2&=&\frac{120\pi}{120\pi}\frac{22000\sqrt{2}}{\sqrt{3}}\frac{\mathrm{d}I_0}{\mathrm{d}\tau}\tag{11}\\\\\frac{220000\sqrt{2}}{\sqrt{3}}(V_2-V_1)&=&\frac{120\pi}{120\,n\,\pi}\frac{22000\sqrt{2}}{\sqrt{3}}\frac{\mathrm{d}I_1}{\mathrm{d}\tau}\tag{12}\\\\\frac{120\pi}{1.2\times 10^{4}\pi}\frac{220000\sqrt{2}}{\sqrt{3}}\frac{\mathrm{d}V_2}{\mathrm{d}\tau}&=&\frac{22000\sqrt{2}}{\sqrt{3}}I_2\tag{13}\\\\\frac{120\pi}{1.2\times 10^{4}\,m\,\pi}\frac{220000\sqrt{2}}{\sqrt{3}}\frac{\mathrm{d}V_1}{\mathrm{d}\tau}&=&\frac{22000\sqrt{2}}{\sqrt{3}}I_1\tag{14}\\\\I_0&=&I_1+I_2\tag{15}\end{eqnarray}
整理すると
\begin{eqnarray}\frac{1}{10}\frac{\mathrm{d}I_0}{\mathrm{d}\tau}&=&\frac{1}{10}\cos{\tau}-V_2\tag{16}\\\\\frac{1}{10\, n}\frac{\mathrm{d}I_1}{\mathrm{d}\tau}&=&V_2-V_1\tag{17}\\\\\frac{\mathrm{d}V_2}{\mathrm{d}\tau}&=&10 I_2\tag{17}\\\\\frac{\mathrm{d}V_1}{\mathrm{d}\tau}&=&10\, mI_2\tag{19}\\\\I_0&=&I_1+I_2\tag{20}\end{eqnarray}
(16)~(20)式が演算方程式となる。
2.2 ブロックダイヤグラム
演算方程式をもとにブロックダイヤグラムを組むと、以下のようになる。
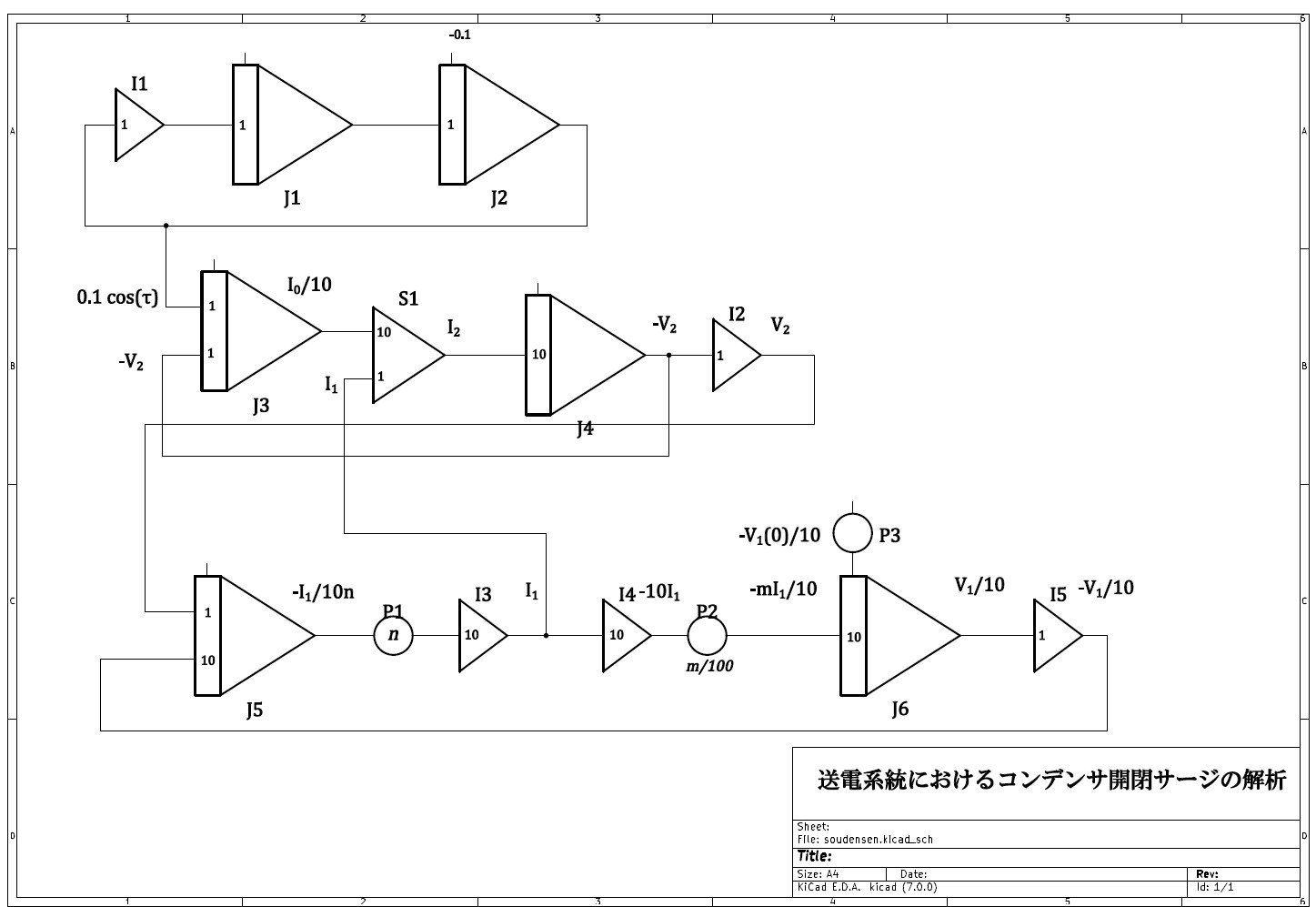
図 2
係数ポテンショメータでmやnの値を変えながら応答を調べることができる。
3.結果
\(n=0.04, m=60\)とし、\(V_1\)の初期値として0.08を選んだ場合の、低速モードにおける\(I_2\,,V_2\,,-V_1\) の演算結果を図3に示す。各波形ごとにスケールが違うことに注意されたい。
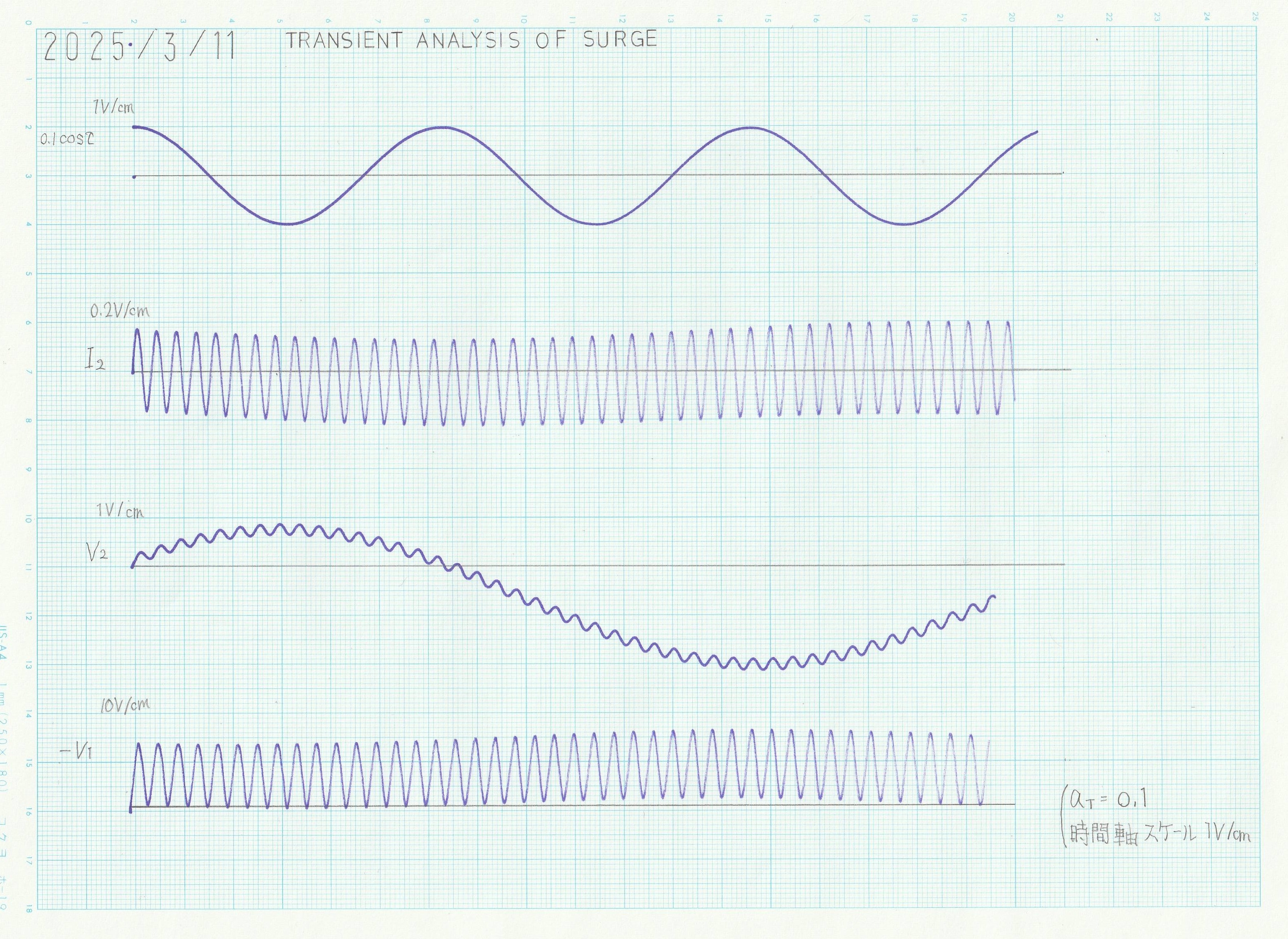
図3
低圧側の波形\(V_1\)に、高圧側の波形\(V_2\)の波形よりも大きい高周波過渡電圧が重畳していることがわかる。この過電圧はコンデンサ\(C_1\)の初期電圧によっても大きく異なる。
参考までに、文献[1]に掲載されている、\(n=0.04, m=60\)のときの電圧・電流波形の低速度型アナログ計算機によるシミュレーション結果を示す。(\(V_1\)などの初期値やレコーダの振幅スケールは不明である。)
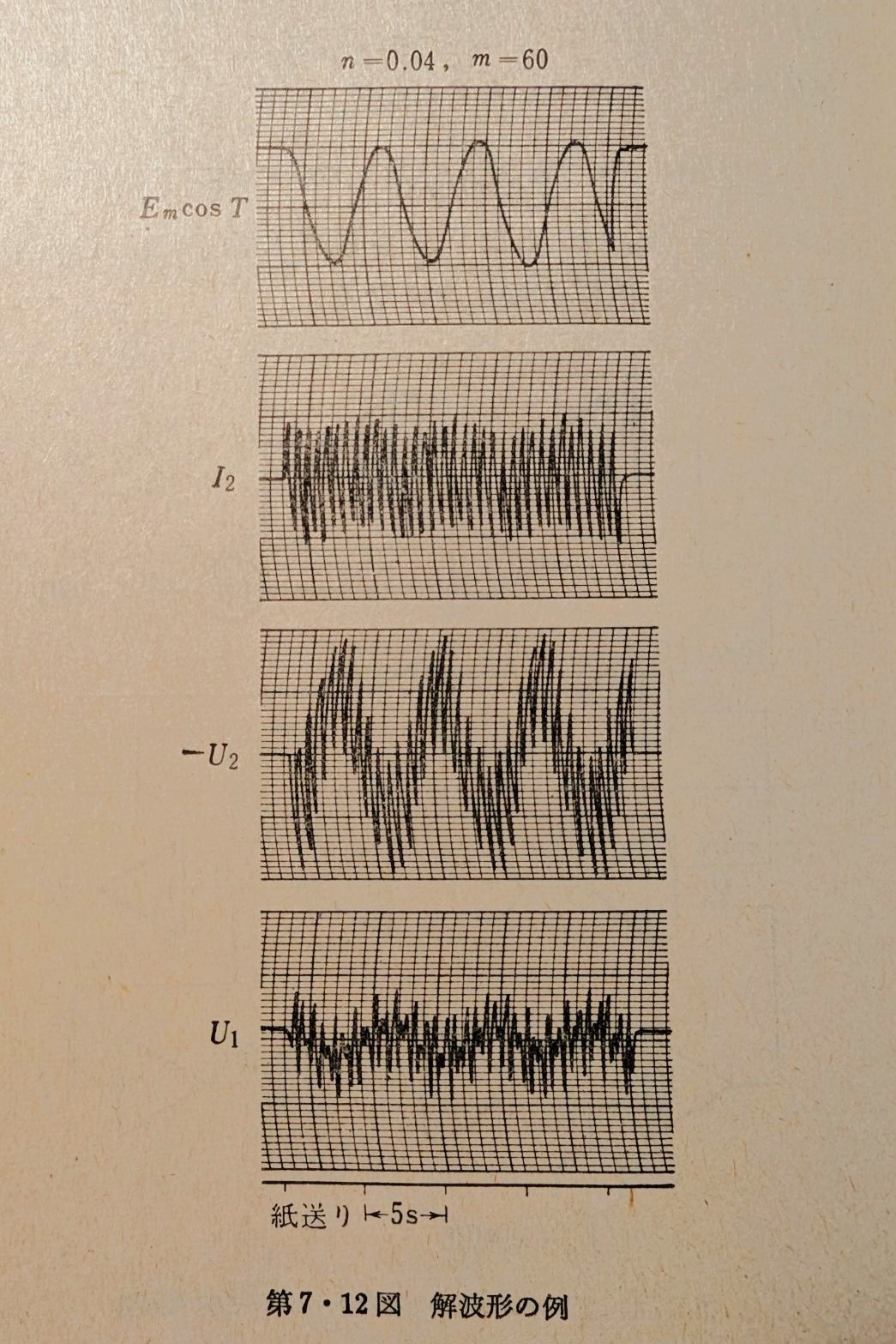
図 3.1
上図はペンの円弧運動により記録する「インク書きペンレコーダ」で記録されたもので、記録波形は信号そのものでなくペンの振れ\(\theta\)の正弦に比例するものであることに注意。上図中\(U_1,U_2\)はそれぞれ\(V_1,V_2\)に対応する。
4.参考文献
[1] 長森亨三, 木地和夫. 「アナログ計算機入門」第8版, オーム社, 1966
[2]大久保 保仁.「新ユニバーシティ 電力システム工学」第1版, オーム社, 2021.