Weberの微分方程式と放物柱関数
目次
1.準備
Weberの微分方程式
\[\frac{\mathrm{d}^2y}{\mathrm{d}z^2}+\left(\nu+\frac{1}{2}-\frac{1}{4}z^2\right)y=0\tag{1}\]
の解は放物柱関数(またはWeber関数とも呼ばれる) \(\mathrm{D}_{\nu}(z)\) と \(\mathrm{D}_{-\nu-1}(i\,z)\)の線形結合となる。(1)のような微分方程式は放物柱座標 (parabolic cylindrical coodinate) でヘルムホルツ方程式を変数分離した際に現れる。[2]
(Weber-Lommel関数 \(\mathrm{E}_{\nu}(z)\)とは別物であるが、どちらもWeber関数と呼ばれることがあるので注意。\(\mathrm{D}_{\nu}(z)\)はHeinrich Martin Weberにちなみ、\(\mathrm{E}_{\nu}(z)\)は Heinrich Friedrich Weberに由来する。)
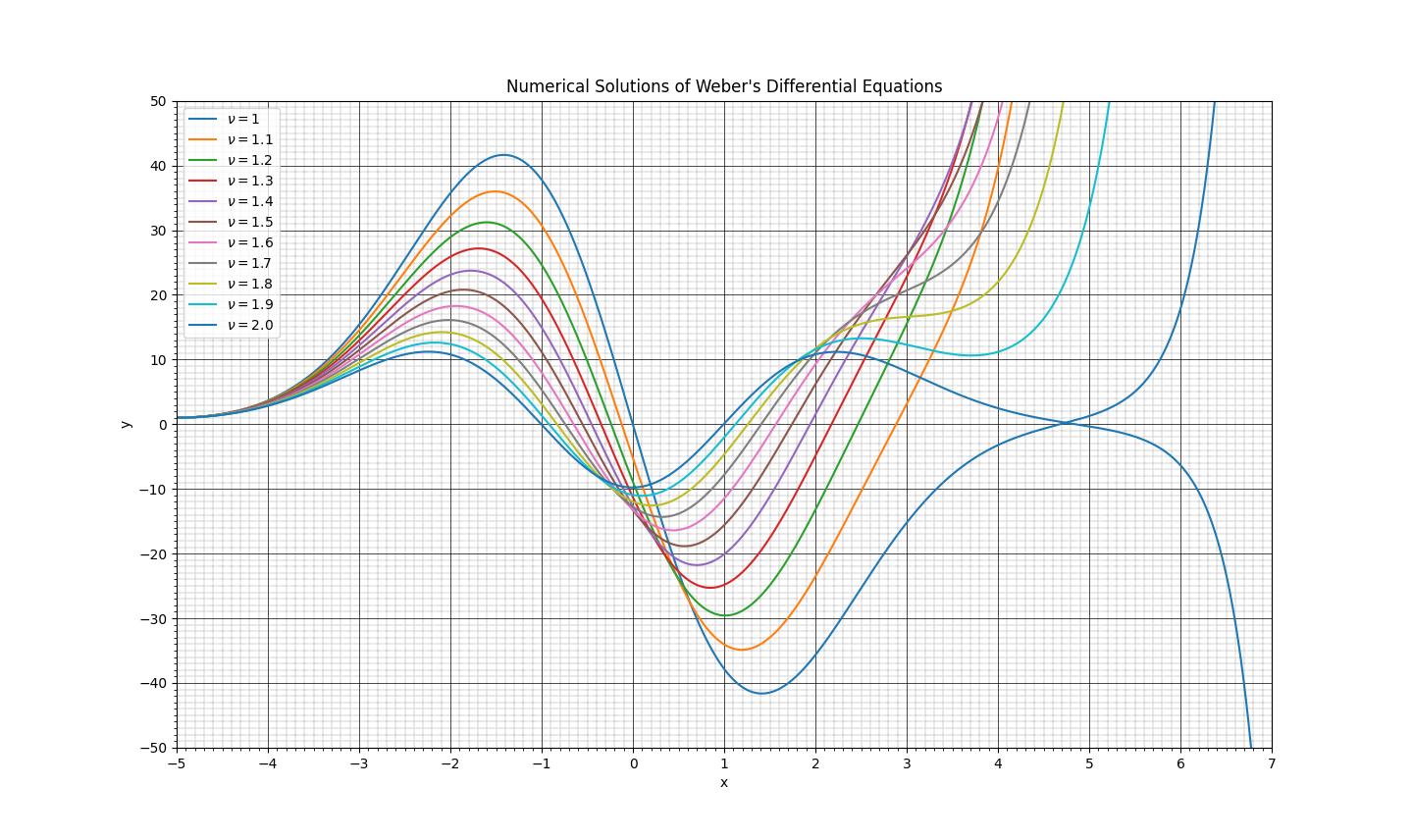
図1 Weberの微分方程式の数値解(4次ルンゲクッタ法使用)
2.アナログコンピュータプログラム
\(\nu\)を正の実数、\(t\)を独立変数とする。
\[\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\left(\nu+\frac{1}{2}-\frac{1}{4}t^2\right)x=0\tag{2}\]
Weberの微分方程式(2)を原方程式としてアナログコンピュータでの演算を試みる。ベッセルやケルビンの微分方程式のように係数に極がある方程式ではないので大変ありがたい。陽関数法で実装でき、マシューの微分方程式と同じトポロジーの演算回路で済む。すなわち、2階微分方程式\(y''=-f(t)\,y\)の演算回路に外力項\(f(t)\)を乗算器で掛ける手法である。
スケーリングを容易にするため、パラメータの範囲は\(1\leq{\nu}\leq{2}\)に限定し、独立変数の範囲は \(-5\leq{t}\leq{5}\)、初期条件は\(y(-5.0)=1\,,y'(-5.0)=0\)とおいた。
2元連立系に直せば
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}=&y\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=&\displaystyle-\left(\nu+\frac{1}{2}-\frac{1}{4}\,t^{2}\right)x\end{cases}\tag{3}\end{eqnarray}
演算方程式に変換すると、
\begin{eqnarray}\begin{cases}\displaystyle\frac{a_{\tau}}{a_{X}}\frac{\mathrm{d}X}{\mathrm{d}\tau}=&\displaystyle\frac{Y}{a_{Y}}\\\\\displaystyle\frac{a_{\tau}}{a_{Y}}\frac{\mathrm{d}Y}{\mathrm{d}\tau}=&\displaystyle-\left(\nu+\frac{1}{2}-\frac{1}{4\,a_{T^{2}}}\,T^{2}\right)\frac{X}{a_{X}}\end{cases}\tag{4}\end{eqnarray}
\(x\) や \(y\) の演算単位を50に対応させ、\(a_{X}\,,a_{Y}=1/50\) とする。低速モードでの時間換算係数は\(a_{\tau}=2\)をすることで、\(t=-5\)から\(t=5\)までを20秒で演算させる。独立変数の電圧換算係数は\(a_{T}=1/5\;a_{T^2}=1/25\)である。以上を(4)式に代入すると、
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=&0.5\,Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=&\displaystyle-0.5\,\left(\nu+0.5-6.25\,t^{2}\right)X\end{cases}\tag{5}\end{eqnarray}
\(-0.5\,\left(\nu+\frac{1}{2}-6.25\,t^{2}\right)\)は電圧信号として過大であるので、半分にスケーリングしてから、\(X\)と掛け合わせたのち、積分器の2倍入力端子に入力させることとする。すなわち、
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=&0.5\,Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=&\displaystyle-2\left\{0.25\,\left(\nu+0.5-6.25\,t^{2}\right)X\right\}\end{cases}\tag{6}\end{eqnarray}
演算回路は図のようになる。
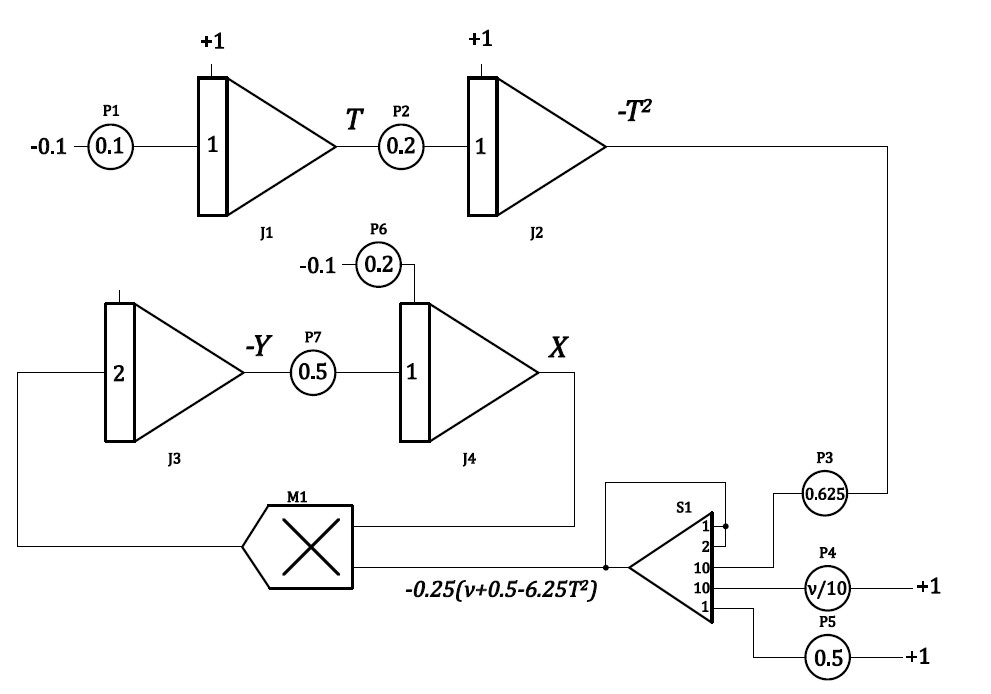
図2 ブロックダイヤグラム
加算器では、\(\frac{1}{4}\)のスケーリングをフィードバックによる方法で実現している。\(X\)の初期条件は50でスケーリングされ、0.02となっている。
独立変数項 \(T^{2}\) の発生にも注意が必要である。積分器\(\mathrm{J_1}\), \(\mathrm{J_2}\)は演算方程式
\begin{eqnarray}\frac{a_{\tau}}{a_{T}}\frac{\mathrm{d}T}{\mathrm{d}\tau}=&1\tag{7}\\\\\frac{a_{\tau}}{a_{T^{2}}}\frac{\mathrm{d}T^{2}}{\mathrm{d}\tau}=&2\frac{T}{a_{T}}\tag{8}\end{eqnarray}
をそれぞれ表している。整理すると、
\begin{eqnarray}\frac{\mathrm{d}T}{\mathrm{d}\tau}&=&\frac{a_{T}}{a_{\tau}}=\frac{1}{5}\cdot\frac{1}{2}=0.1\tag{9}\\\\\frac{\mathrm{d}T^{2}}{\mathrm{d}\tau}&=&2\,\frac{a_{T^{2}}}{a_{T}}\cdot\frac{T}{a_{\tau}}=2\,\frac{5}{25}\cdot\frac{T}{2}=0.2\,T\tag{10}\end{eqnarray}
である。
3.結果
低速モードにおける、\(\nu=1.0\) から 、\(\nu=2.0\) までの解を示す。
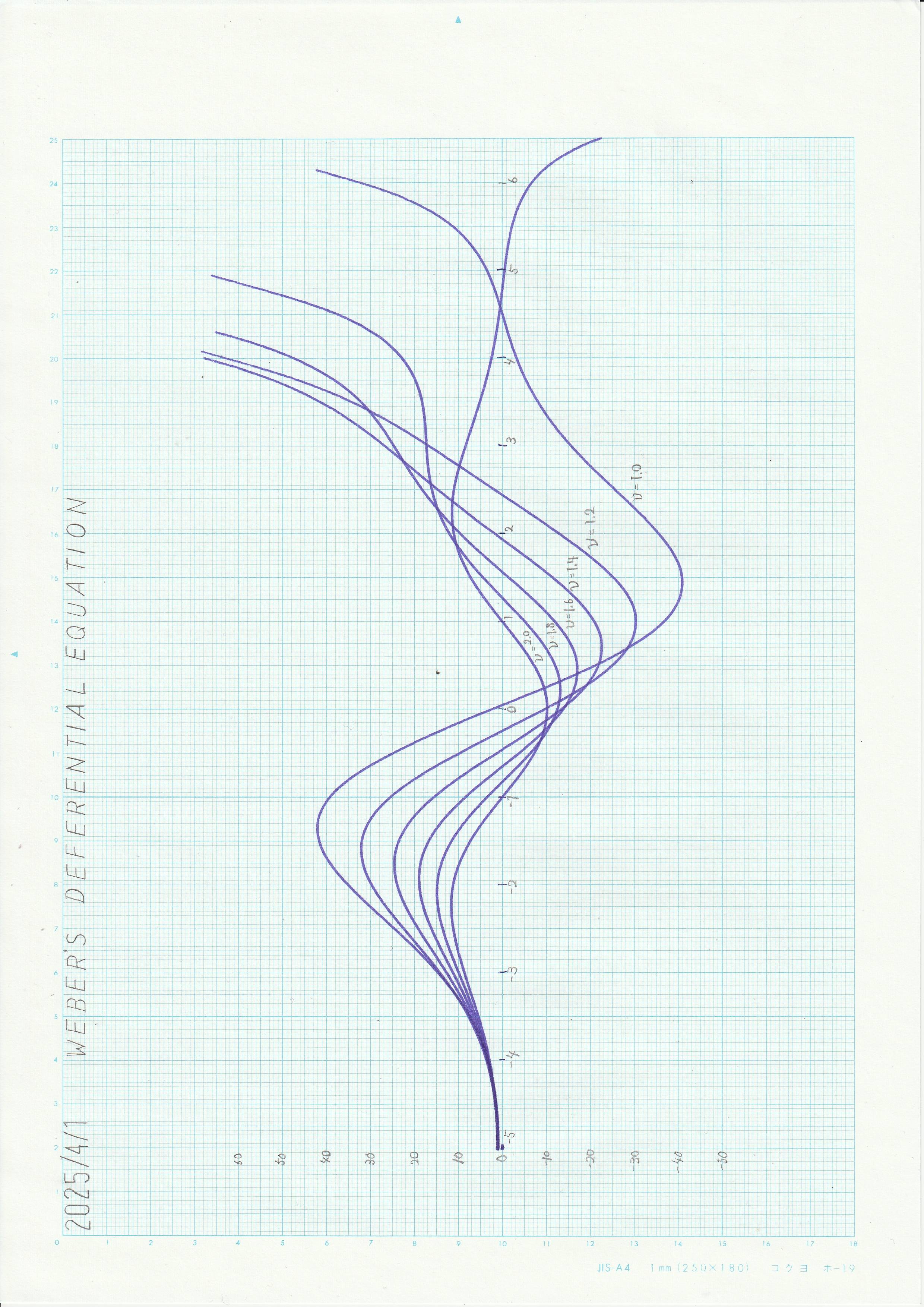
図3 低速モードでの解
高速モードで \(\nu=1.4\) の時の解を表示させた場合のオシロスコープ画面を図4に示す。
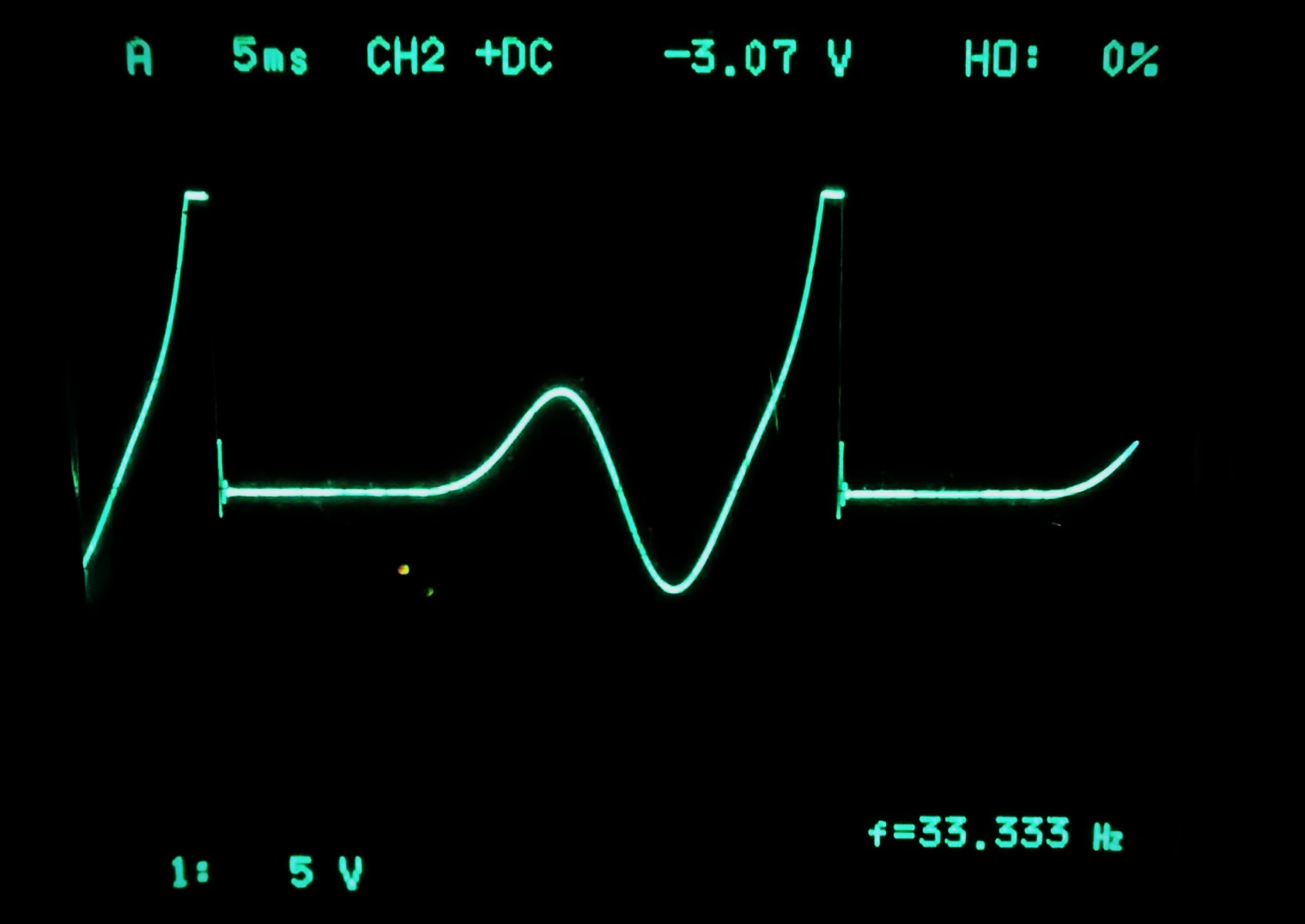
図4 ν=1.4の時の解
アナコン実験の最中に気づいたことだが、\(\nu=1.0\) や \(\nu=2.0\)のようなパラメータ値での解は、他の中途半端な \(\nu\) の場合に比べ、\(\nu\)の値(というか \(x\) にかかる変数係数全体の値)の微小擾乱に対しかなり敏感になっているようにおもえた。(なので精密な係数設定に難儀した。)
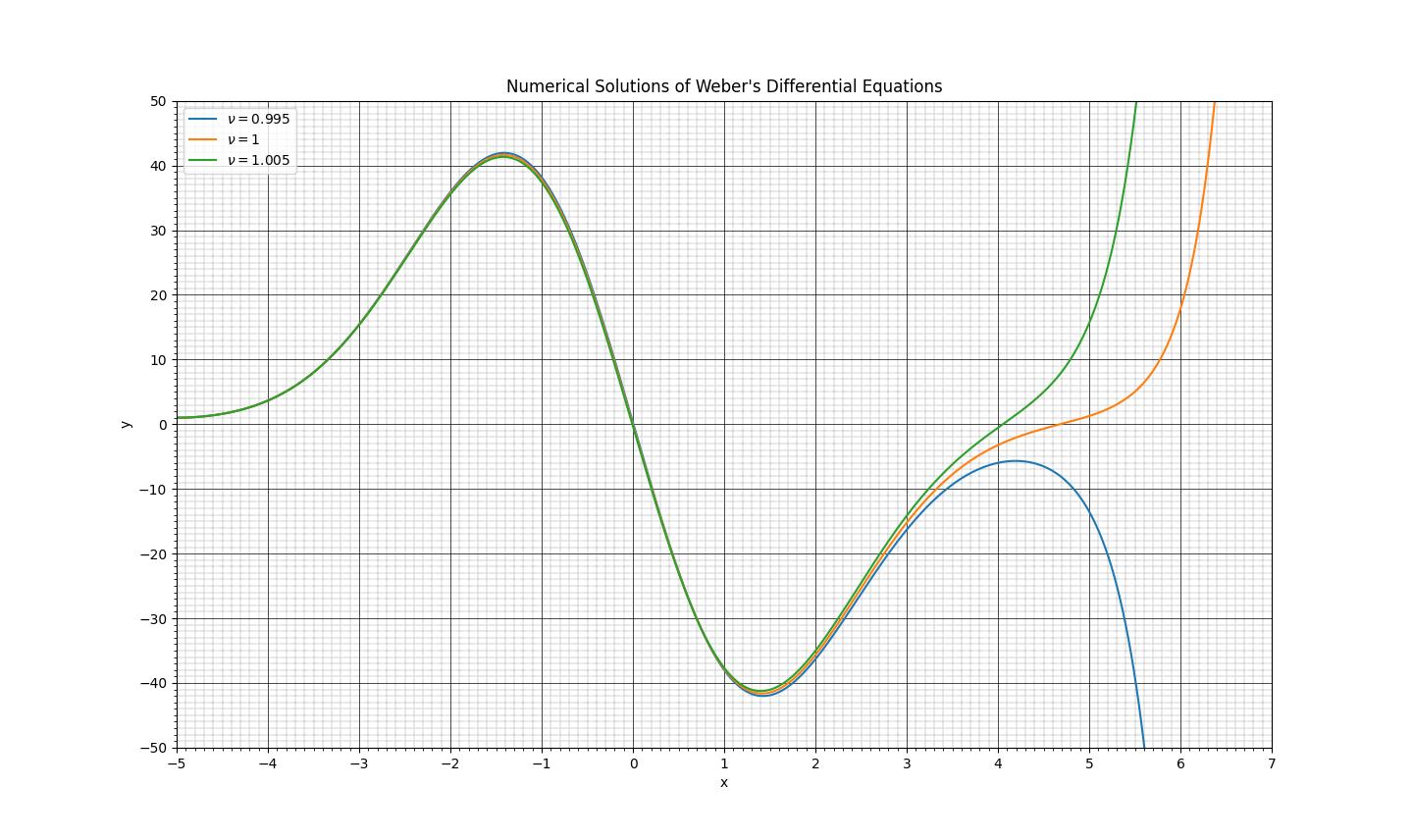
これはよく考えてみれば当然である。通常の単振動の場合での各加速度(の2乗)に相当する部分 \(\left(\nu+\frac{1}{2}-\frac{1}{4}\,t^{2}\right)\) が正の部分(\(t=0\)の周辺)で系は安定だが、それ以外の大部分で負の値であり、解は発散する。\(t=0\) を越してどんどん大きくなるにつれ、発散の度合いは大きくなる。それは別に\(\nu\) の値に依らずどんな場合でもいえるわけだが、 \(t\) の値が0より大きいときの解が飽和せず画面上に残っているのが今回 \(\nu=1.0\) や \(\nu=2.0\) しかなく、現象が目立ったのがそれらの場合だっただけなのだ。
また、\(\nu\) が大きくなるにつれ、上に凸な放物線 \(\left(\nu+\frac{1}{2}-\frac{1}{4}\,t^{2}\right)\) は上方にシフトするため、安定な振動を維持する時間が長くなる。
4.参考文献
[1] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」第1版, 岩波書店, 1975.
[2] F. M. Arscott. "The Land Beyond Bessel: A Survey of Higher Special Functions." In Ordinary and Partial Differential Equations Proceedings of the Sixth Conference Held at Dundee, Scotland, New York: Springer-Verlag,pp 26-45, 1980.
[3] Weisstein, Eric W. "Weber Differential Equations." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/WeberDifferentialEquations.html
[4] Weisstein, Eric W. "Parabolic Cylinder Function." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/ParabolicCylinderFunction.html