ファンデルワールスの状態方程式
目次
1.ファンデルワールスの状態方程式
分子間力や気体分子自体の体積を考慮しない場合の気体の状態方程式は、気体の圧力を \(P\)[Pa] 、体積を \(V\)[m^3/mol] 、温度を \(T\)[K]、気体定数を \(R\)[J/(K・mol)]として
\[PV=RT\tag{1}\]
で表される。温度をパラメータとしてP-Vグラフを描くと、反比例のグラフとなる。
\(a\) を分子間引力による効果を示すパラメータで、\(b\) を気体分子の体積排除効果を示すパラメータとすれば、実在気体の状態方程式は
\[\left(P+\frac{a}{V^2}\right)\left(V-b\right)=RT\tag{2}\]
となる(ファンデルワールスの状態方程式)。(2)式をアナログコンピュータで解き、複数の \(RT\) の値でP-V線図を描画する。
2.アナログコンピュータプログラム
方程式(2)を変形する。
\begin{eqnarray}\left(P+\frac{a}{V^2}\right)\left(V-b\right)-RT=0\\\\\frac{a}{V}\left(1-\frac{b}{V}\right)+P\,\left(V-b\right)-RT=0\tag{3}\end{eqnarray}
式(3)の右辺の0を高利得増幅器(もしくは時定数小の積分器)の入力とおく陰関数法を利用して解く。(この手法の他にも、陽関数法による実装・最急降下法による実装も可能である。)体積 \(V\) を独立変数とする。\(V=0\) で \(P\) の値は無限大になるため、\(V\gt{0}\) の適当な点から0に向かって掃引することとした。
ブロックダイヤグラムは以下の通り。
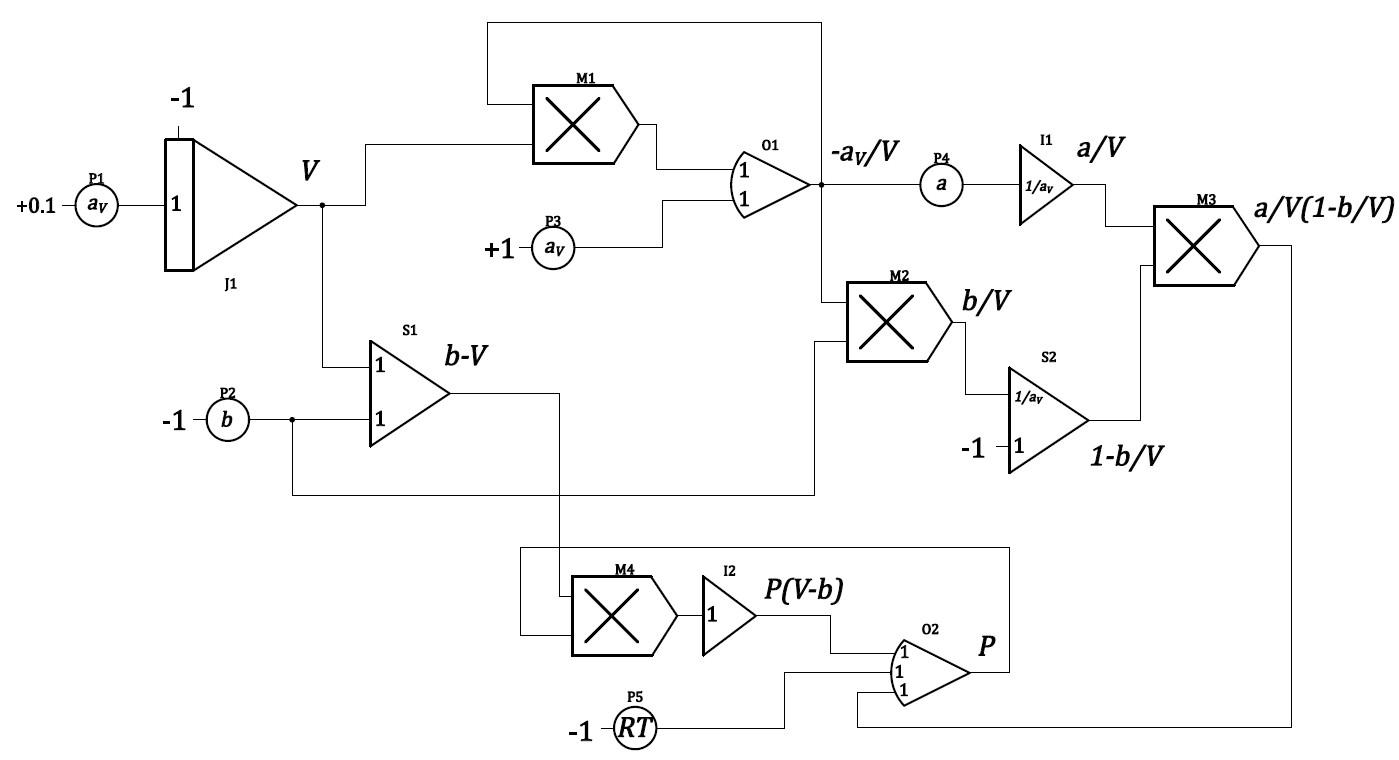
\(a_{V}\) は 通常における\(a_{T}\) と同様の扱いで、独立変数の電圧換算係数である。
パラメータ \(a\)、\(b\) については、実際の気体での値よりも大きくとり、グラフの特徴が顕著になるよう\(RT\)も試行的に定めた。
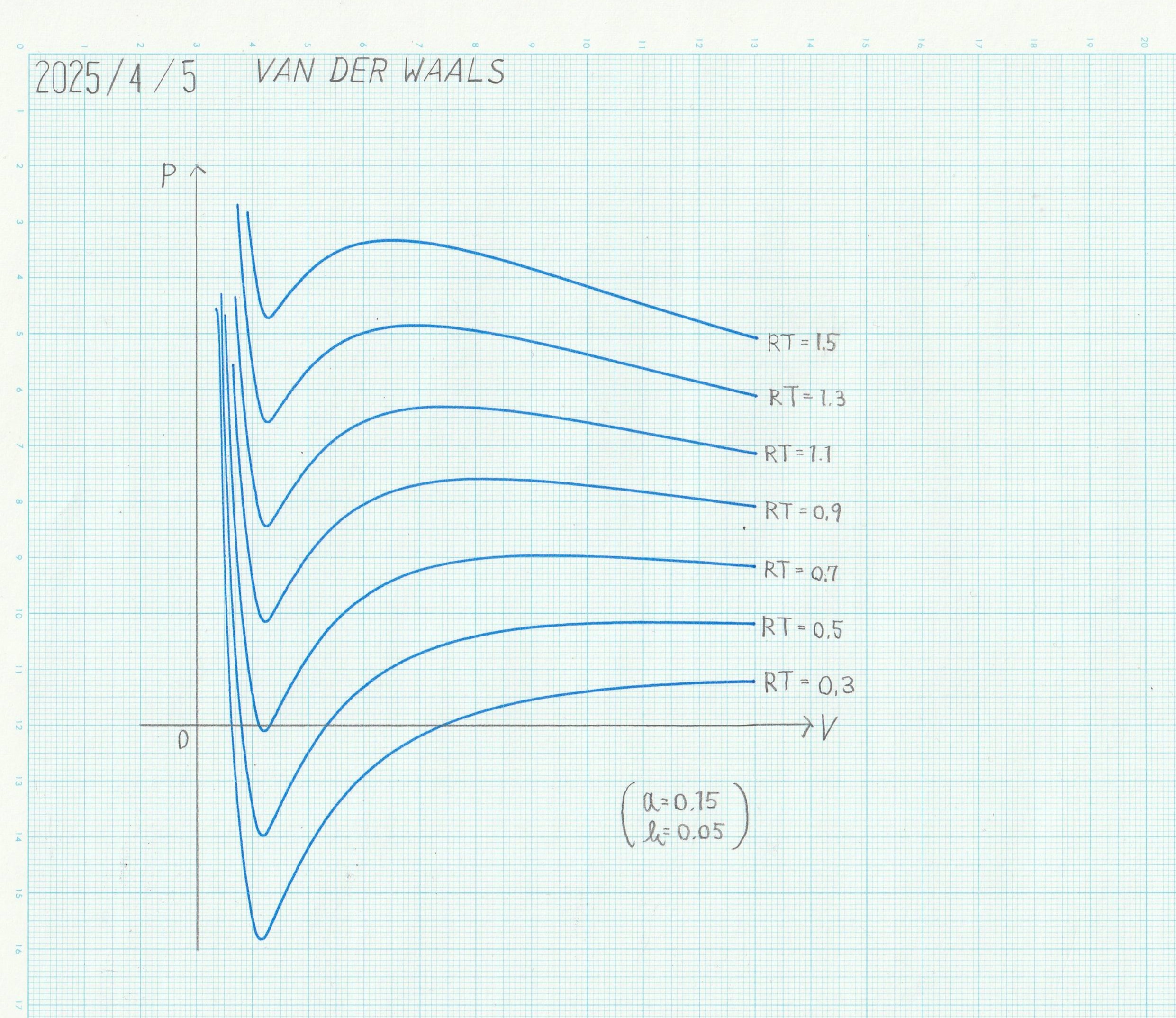
3.結果
低速モードにおける演算結果(P-V線図)を下に示す。諸係数は、\(a_{V}=1/20\), \(a_{\tau}=1\), \(a=0.15\), \(b=0.05\) と設定した。
4.参考文献
[1] 本田昭. 「シミュレーション技術を学ぶためのアナログコンピュータの基礎と演習」第1版, コロナ社, p143-p145, 1976.