一機無限大母線系統の過渡安定度
目次
1.動揺方程式の導出とスケーリング
今回は、自作アナログ計算機により電力系統過渡安定度の解析を行う。一機無限大母線 (SMIB: Single Machine Infinite Bus) 系統における電力動揺方程式(Swing Equation)[1]を導出し、演算方程式に変換してシミュレーションを行う。
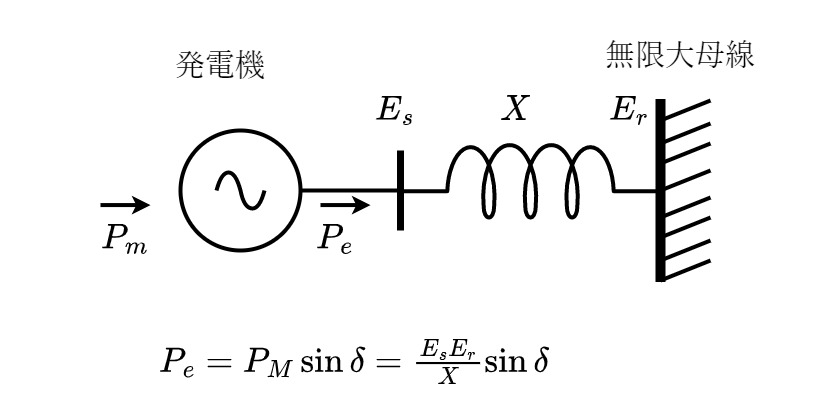
図1 対象とする電力系統の模式図
同期発電機の回転慣性モーメントを \(J\,[\text{kg}\cdot\text{m}^2]\)、回転子の回転角(機械角)を \(\theta\,[\text{rad}]\)、機械的入力トルクを \(T_m\,[\text{N}\cdot\text{m}]\)、電気的出力トルクを \(T_e\,[\text{N}\cdot\text{m}]\) とすると、次の関係が成り立っている。
\[J\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}=T_m-T_e\tag{1}\]
機械角を電気角 \(\delta\,[\text{rad}]\) に変換し、(1)の両辺に角速度 \(\omega_{s} \,[\text{rad}/\text{s}]\) を掛けパワーの次元にすると
\[\omega_{s}J\frac{\mathrm{d}^2\delta}{\mathrm{d}t^2}=P_m-P_e\tag{2}\]
ただし、\(P_m \,[\text{J}/\text{s}]=\omega_s\,T_m\)、\(P_e \,[\text{J}/\text{s}]=\omega_s\,T_e\) としている。
慣性定数 \(H\,[\text{W}\cdot\text{s}]=J\omega_{s}^2/2S_{\text{base}}\) (ただし \(S_{\text{base}}\,[\text{VA}]\) は定格皮相電力) を用いた表現は
\[\frac{2H}{\omega_{s}}\frac{\mathrm{d}^2\delta}{\mathrm{d}t^2}=P_m-P_e\tag{3}\]
となり、左辺の2階微分の係数をまとめて慣性係数 \(M\) \([\text{W}\cdot\text{s}^2]\) としておけば
\[M\frac{\mathrm{d}^2\delta}{\mathrm{d}t^2}=P_m-P_e\tag{4}\]
と表される。ここで、電気的出力 \(P_{e}\) (有効電力)が
\[P_{e}=P_{M}\sin{\delta}\tag{5}\]
の形で表されることから、(4)式は
\[M\frac{\mathrm{d}^2\delta}{\mathrm{d}t^2}=P_m-P_M\sin{\delta}\tag{6}\]
となる。(6)式が(制動項なしの)電力動揺方程式であり、(6)式を解くことで位相角の時間発展を調べることができる。負荷の急変、もしくは故障により、有効電力 \(P_e\) が急減してしまうと、(6)式より同期機のローターが加速し、位相の動揺が発生することが分かる。その後リアクタンスが回復すれば、ローターは減速に転じる。回復が間に合って再び定常に戻れば安定するが、それが間に合わないと脱調してしまう。系統事故発生後に位相角が動揺しても発電機が同期運転を継続できる度合を過渡安定度いう。系統の安全な運用のためには過渡安定度を高めることが重要である。
(6)式は2階の非線形微分方程式であるから解析解を得ることは難しい(厳密には可能だが、初等関数のみでは表せない)。数値計算に頼るのが一番だが、三角関数回路さえあればアナログ計算機でも十分対応可能な問題である。

図 アナログ式三角関数回路(入力電圧の正弦・余弦を出力可能)
2.エネルギー関数と分岐
非減衰の動揺方程式(6)について、\(v=\frac{\mathrm{d}\delta}{\mathrm{d}t}\) を用いた式に直すと
\[Mv\frac{\mathrm{d}v}{\mathrm{d}\delta}=P_m(1-m\sin{\delta})\tag{7}\]
上式を、平衡点 \(\delta_{0}\)から\(\delta\)まで積分すると、以下のようなエネルギーの式が得られる。
\[\frac{1}{2}Mv^2-P_m\biggl\{\left(\delta+m\cos{\delta}\right)-\left(\delta_0+m\cos{\delta_0}\right)\biggr\}=0\tag{8}\]
ここで、
\[K(\delta)=\frac{1}{2}Mv^2\tag{}\]
は同期機の回転子の運動エネルギーであり、
\[U(\delta)=-P_m\left(\delta+m\cos{\delta}\right)\tag{9}\]
は系統の相差角を\(\delta\)だけ開くために要するエネルギーである。
\(\delta_0\) についての項を初期値とみなせば、系統全体のエネルギー \(V=K+U\) が常に一定に保たれることを表している。
\[\frac{1}{2}Mv^2+U(\delta)=\text{const}\tag{10}\]
\(V\)がある一定値をとる点を結んだ曲線を位相面軌跡(phase plane trajectory)という[2]が、相平面上において(平衡点以外の)初期値を与えた場合の(6)式の解軌道は、初期値を通る位相面軌跡と一致する。
\(m=P_M/P_m\) の値によって位相面軌跡を分類すると、\(m=1\)を境界として分岐(bifurcation)が生じる。
<1> \(m\lt{1}\) すなわち \(P_{M}\lt{P_m}\) のとき、位相面上ですべての軌道は発散する。機械的入力が最大送電容量より大きい場合であるため、位相は加速し、安全運転が達成できないのは当然である。また、方程式からこの場合平衡点は存在しないことが分かる。
<2> \(m={1}\) すなわち \(P_{M}={P_m}\) は(1)と(3)の境界である。唯一の平衡点 \(\delta=\pi/2\) は鞍点であり、その点を通る軌道自体はホモクリニック軌道となる。
<3> 一方、\(m\gt{1}\) すなわち \(P_{M}\gt{P_m}\) の場合、2つの平衡点(中心点と鞍点)が対となって生じる。その場合の不安定平衡点の位相を\(\delta_{c}\) とし、その点でのエネルギー値を \(V_c\) とすると、エネルギー \(V\) がその臨界値 \(V_c\) より大きいか小さいかで軌道の性質が異なってくる。
・\(V\gt{V_c}\) の場合 : 時間の経過とともに \(v\), \(\delta\) が無限に大きくなり発散する。
・ \(V\lt{V_c}\) の場合 : \(v\), \(\delta\) ともに一定周期で振動する。\(V\) は \(\frac{\partial{V}}{\partial{v}}=\frac{\partial{V}}{\partial{\delta}}=0\) となる点、すなわち平衡点 \((v,\delta)=(0,\arcsin{(1/m)})\) で以下の最小値をとる。\[V_{\text{min}}=-P_m\left(\arcsin{\frac{1}{m}}+\sqrt{m^2-1}\right)\]
・\(V={V_c}\) の場合 : 上記2つの境界(セパラトリクス)であり、\(\delta\lt{\delta_{c}}\) または \(\delta\gt{\delta_c}\) かつ \(v\lt{0}\) のときは常に鞍点( \(\delta=\delta_{c}\))に近づこうとするが、鞍点に到達するには無限の時間が必要であるため、実際の系でこの状態が実現することは無いと考えてよいだろう。
<1>~<3>の位相面軌道の変化は、サドルノード分岐の1種である。また、<3>の場合のエネルギーと位相の臨界値(すなわち鞍点位相角及びその点における全エネルギー)については
\[\delta_{c}=\pi-\arcsin{\frac{1}{m}}\tag{11}\]
\[V_{c}=-P_m\left(\delta_c+m\cos{\delta_c}\right)=-P_m\left(\pi-\arcsin{\frac{1}{m}}-\sqrt{m^2-1}\right)\tag{12}\]
と計算できる。
3.アナログコンピュータによる解析
解析のため、(6)をもとに演算方程式を立てよう。\(\tau=\sqrt{\frac{P_{m}}{M}}t\) なる変数変換を施し、演算時間\(\tau\) を用いて書き改め、さらに \(P_M/P_m=m\) とおくと、
\[\frac{\mathrm{d}^2\delta}{\mathrm{d}\tau^2}=1-m\sin{\delta}\tag{13}\]
と無次元化される。ここで制動巻線、回転子の摩擦による制動項を加えてみる。
\[\frac{\mathrm{d}^2\delta}{\mathrm{d}\tau^2}=1-n\frac{\mathrm{d}y}{\mathrm{d}\tau}-m\sin{\delta}\tag{14}\]
(8)式の \(n\) は制動項の係数、\(m\) は線路リアクタンスに反比例する係数で、これらをパラメータとして(8)を解く。
分かりやすさのために、変数を書き改めて2元連立系に直す。
\begin{cases}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}\tau}&=&y\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}\tau}&=&1-n\,y-m\sin{x}\tag{15}\end{cases}
電圧換算係数を \(a_{X}=a_{Y}=1\)に定めよう。(加速度項は電気信号として現れないのでスケーリングする必要はない。)時間換算係数を\(a_{\tau}=10\) とすれば、演算方程式は
\begin{cases}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}&=&0.1Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}&=&\displaystyle{\frac{1}{10}-\frac{n}{10}\,y-\frac{m}{10}\sin{x}}\tag{16}\end{cases}
となる。
※ \(X\) はラジアン単位である。\(0\leq{x}\leq{\pi}\) 程度の範囲を扱えればよいのだが、\(X\) が現れるのはsin関数の中だけであり、今回使用する自作アナログ計算機の正弦回路は入力1MUが \(\pi\) [rad] に対応しているため、たまたま変数変換をしなくても上手くいくようになっている。
(10)式を実装した演算回路は以下の通り。
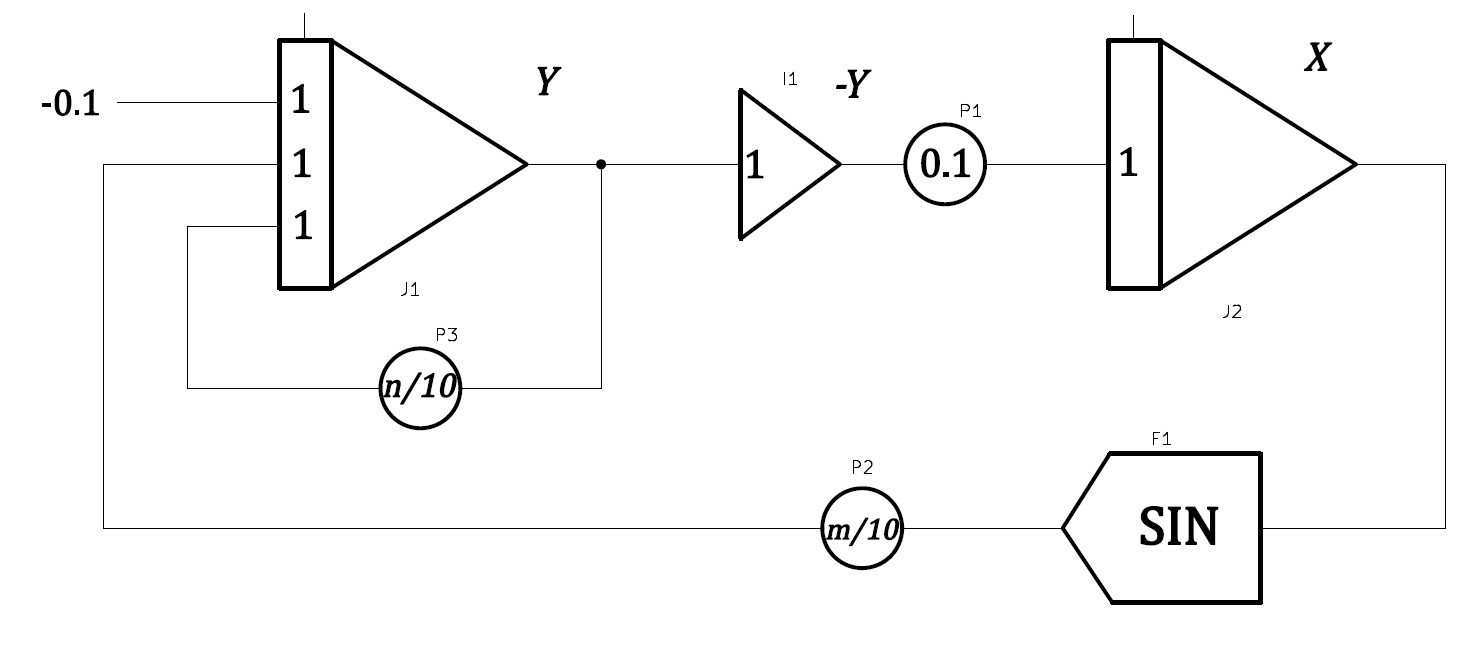
図3 動揺方程式の演算回路ブロックダイヤグラム
3.1 種々の \(m\) の値における演算
\(n=0\) (非減衰)とおいて、 初期条件として \((x_0,y_0)=(0,0)\) を与えた場合の低速演算結果を下に示す。
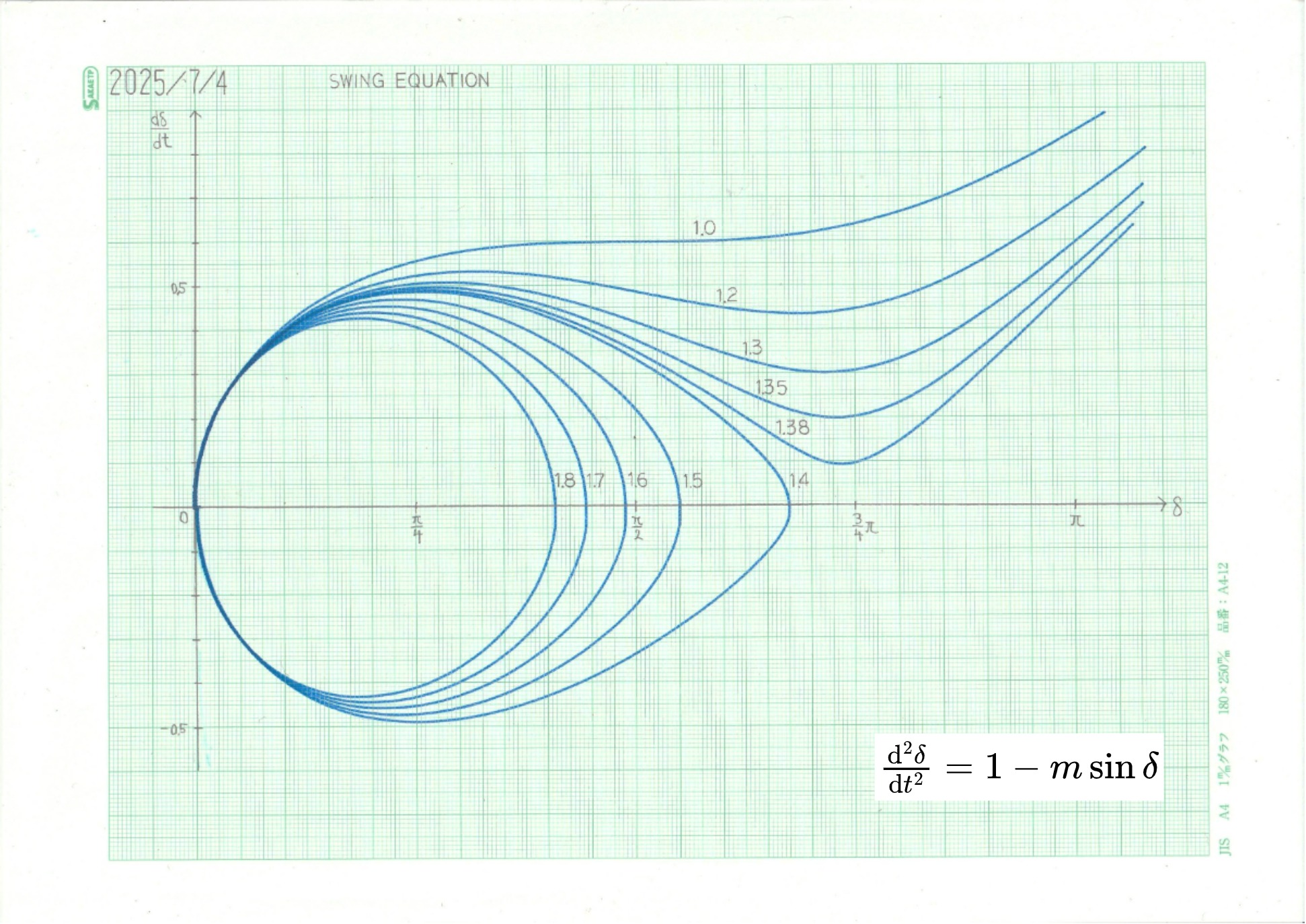
図4 非減衰動揺方程式の解軌道
初期条件を相平面上の原点にとったときの安定限界は \(m=1.39\)から\(m=1.4\)の間であることが分かった。
数値計算による結果も下に示しておく。
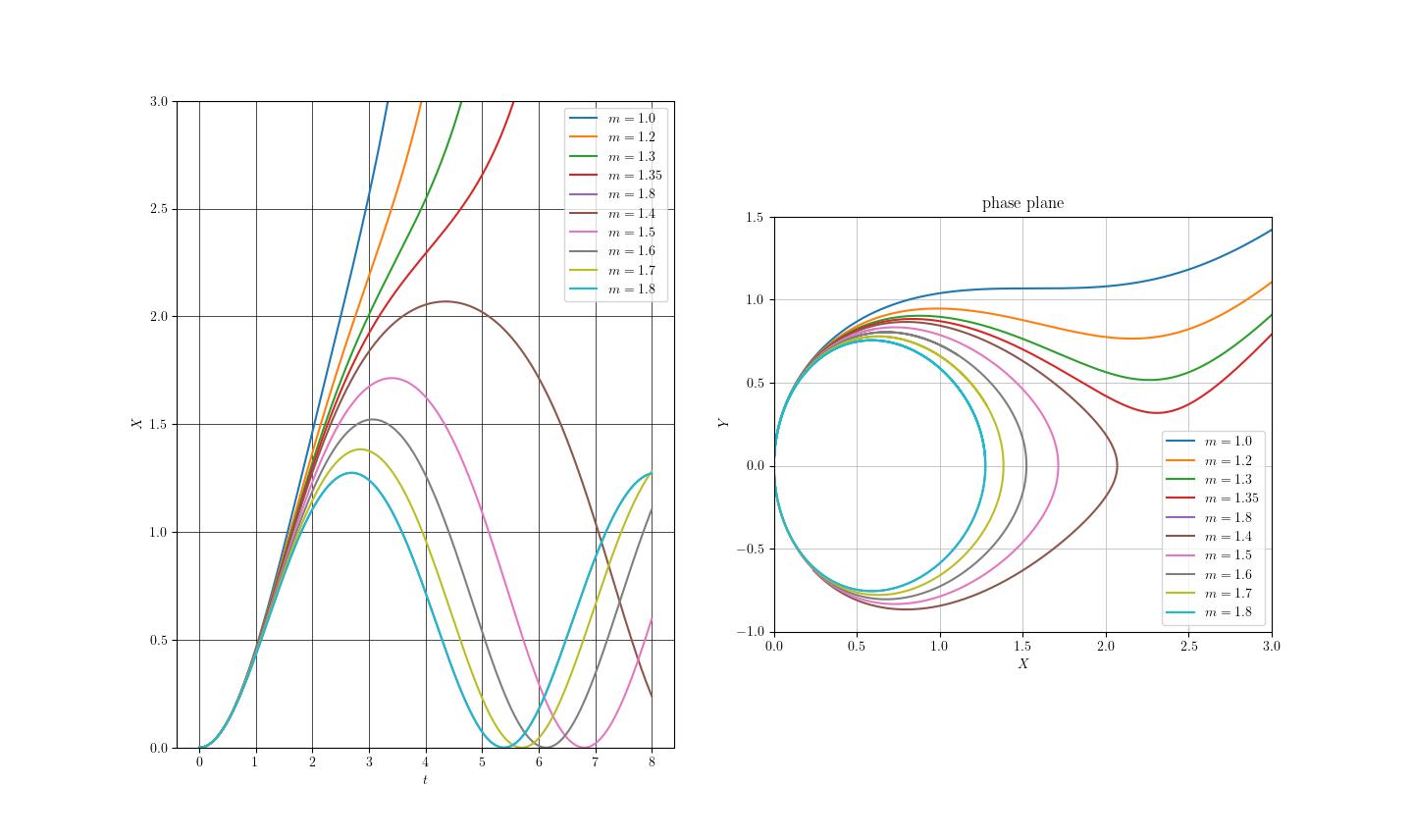
図5 非減衰動揺方程式の数値解(時系列と相平面)
3.2 位相面軌跡と分岐現象
下の図は、\(n=0\)としたときの、\(m\) の値による位相面軌跡の変化を記録したものである。
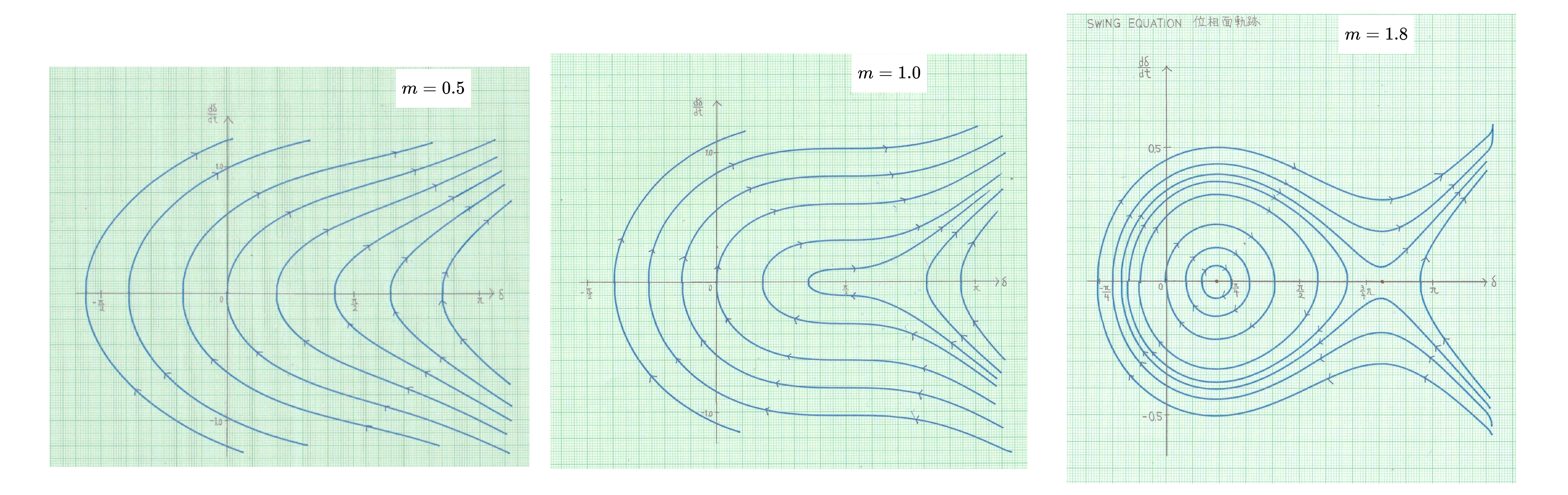
図6 \(m\)が0.5, 1.0, 1.8のときの位相面軌跡
\(m\lt{1}\) の場合は平衡点が無く、\(m=1\) にとなって \(x=\delta=\frac{\pi}{2}\) において平衡点が生じ、\(m\gt{1}\)で安定平衡点と不安定平衡点に分裂する。安定な周期軌道が生じうるのは\(m\gt{1}\)の場合である。各mの値での安定限界を等高線表示したものを図7に示す。XYレコーダに記録した生データに修正を加えた画像である。
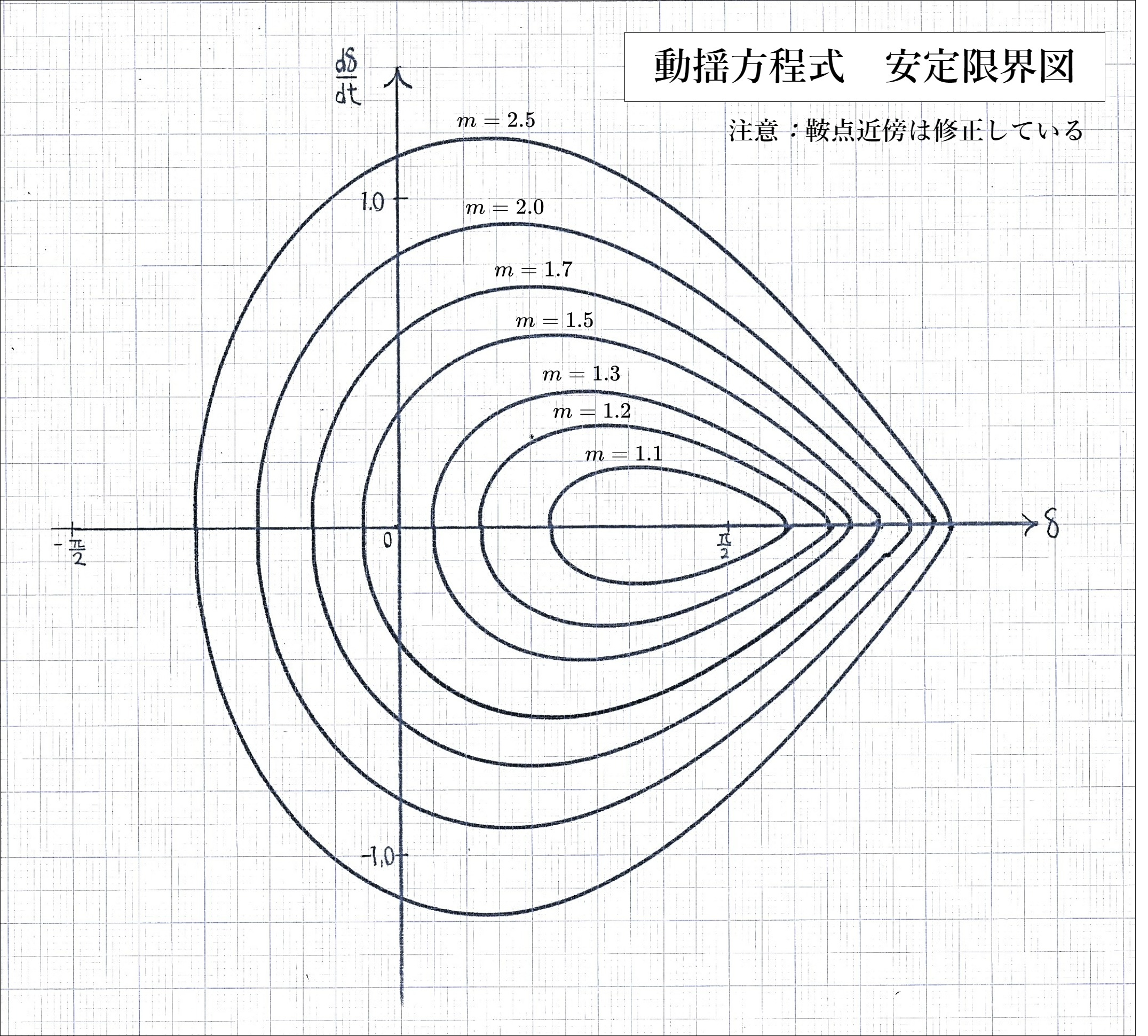
図7 安定限界
また、高速モード(時間換算係数\(a_{\tau}=10^{-3}\))において、その位相面軌跡が変化する様子をパラメータ \(m\)を変えながらリアルタイムに観察することもできる。
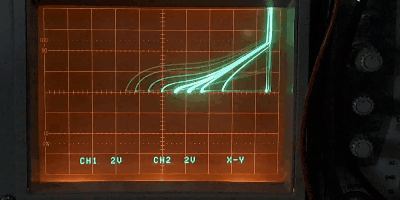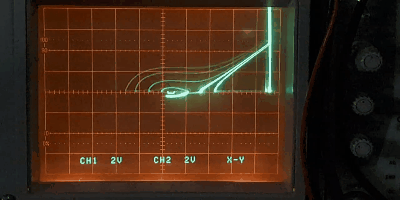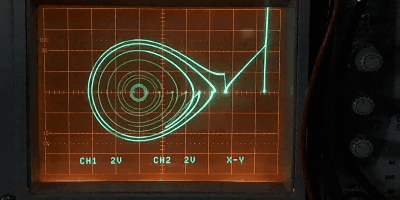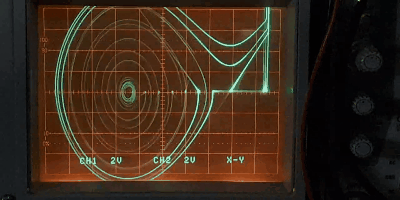
図8 分岐現象
図8は相平面上の軌跡を相差角軸(x軸)に等間隔で並べた初期値を与えて複数表示している。安定平衡点の周りに周期軌道が生じる様子がよくわかる。平衡点の移動の様子は次の画像の方が分かりやすいかもしれない。

図9 平衡点
上の画像では左端の初期値が原点である。各軌道の演算時間範囲は全て等しくしてあるので、軌道ごとの速度ベクトルの大きさが如実に分かる。\(m\) を大きくしていくと、\(m=1\) で \(\delta=\pi/2\)において平衡点が生じ、その後は安定平衡点と不安定平衡点(鞍点)に分裂している。
4.参考文献
[1]大久保 保仁.「新ユニバーシティ 電力システム工学」第1版, オーム社, p81-p84, 2021.
[2] 関根 泰次. 「電力系統解析理論」第1版, 電気書院, p325- p335, 1971.
[3] 小林 英夫, 一柳 勝宏.「電力系統過渡安定度に関するアナログシミュレーション」 愛知工業大学研究報告, 第4巻, p11-p24, 1969.