便利なブロックダイヤグラム集

戻る

単なる備忘録です。いちいち導出するのが面倒なのでまとめました。一般の電子式アナログコンピュータで適用可能なメソッドです。詳細情報については参考文献をご覧ください。

完全に個人用のメモはこっち（見ても面白くない）→自作機EDEQS23専用運用メモ

---

目次

1. ブロックダイヤグラム集
   
   1. 固定係数
   2. 基本関数の発生
   3. ダイオードを利用した非線形演算器
   4. 比較器を利用した非線形演算器
   5. 座標変換・投影
   6. その他便利な回路
2. 参考文献

---

1.ブロックダイヤグラム集

以後、計算機のマシンユニット（演算単位）は10Vであるものとする。

1.1 固定係数

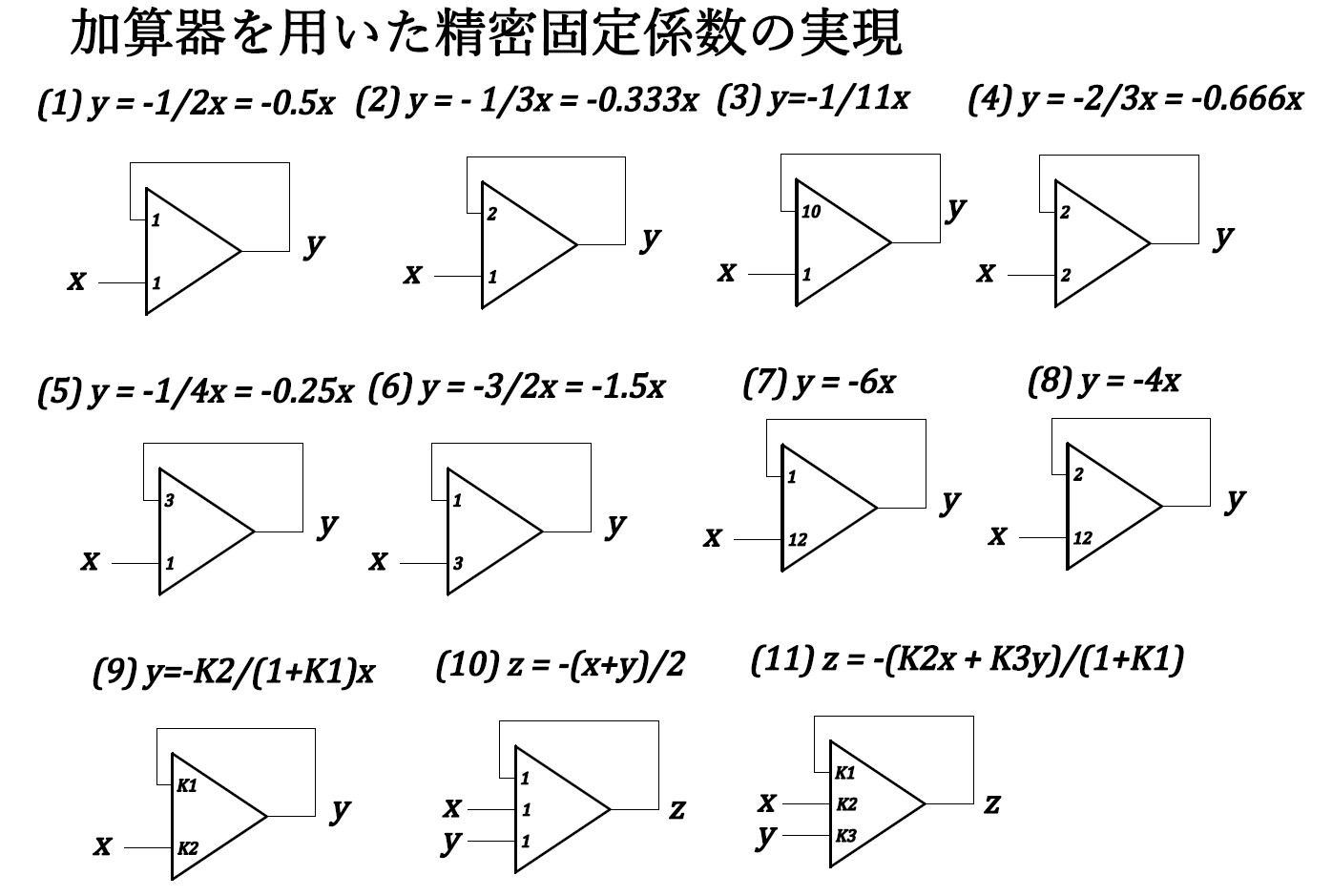
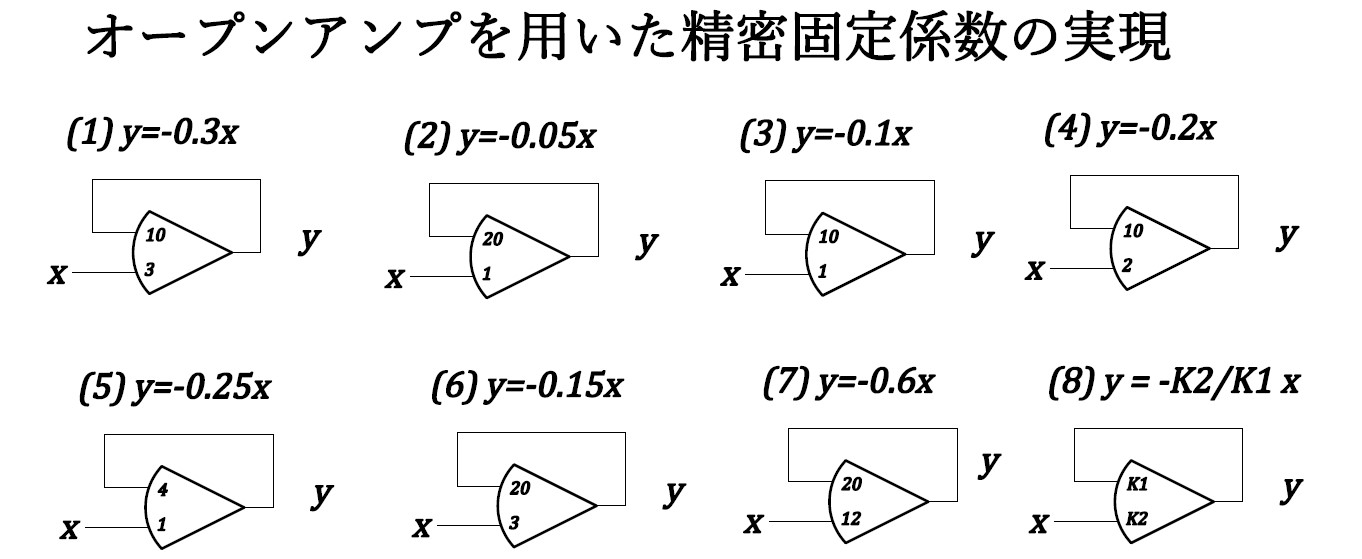
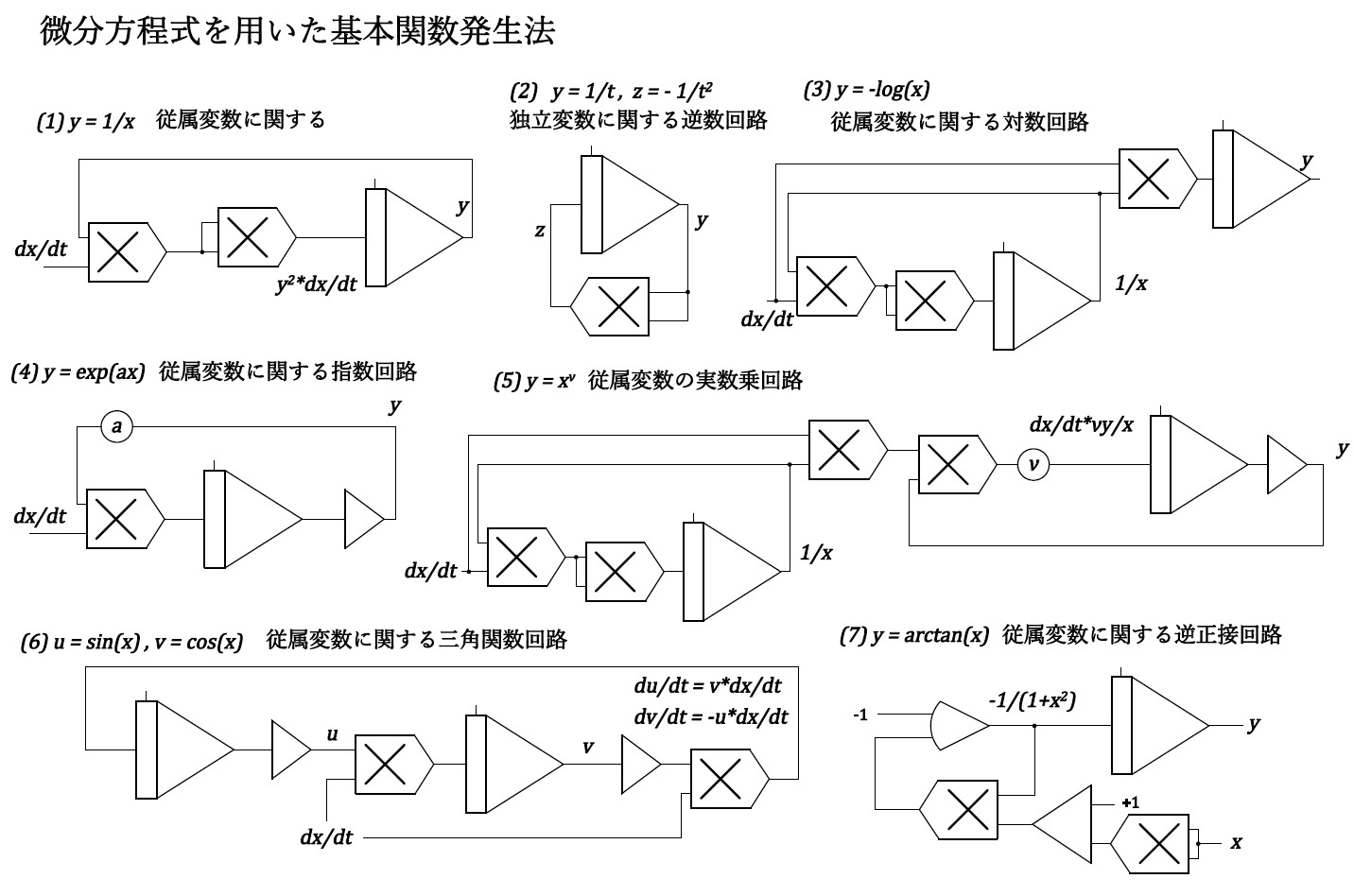
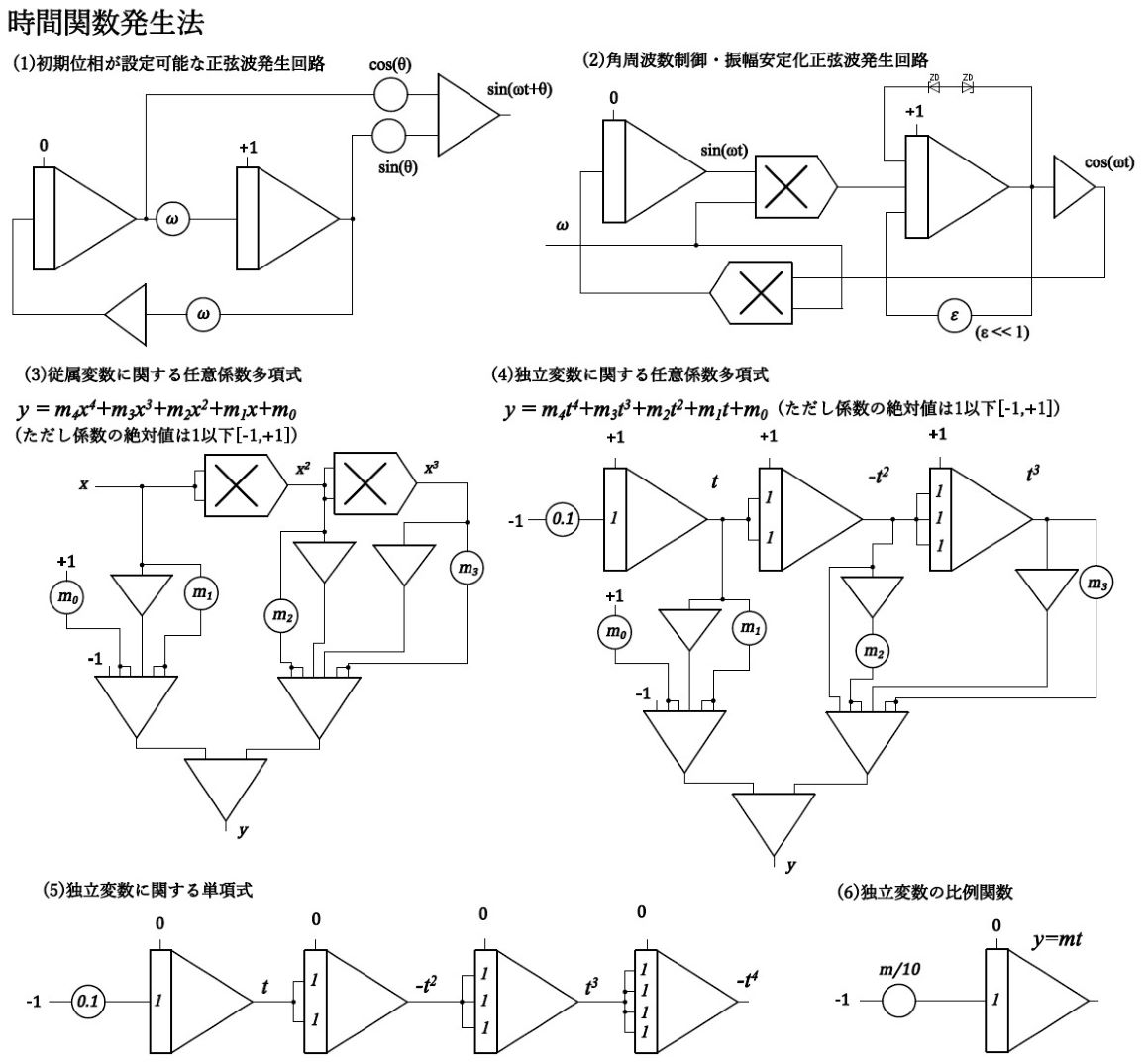
1.2 基本関数の発生

 

 

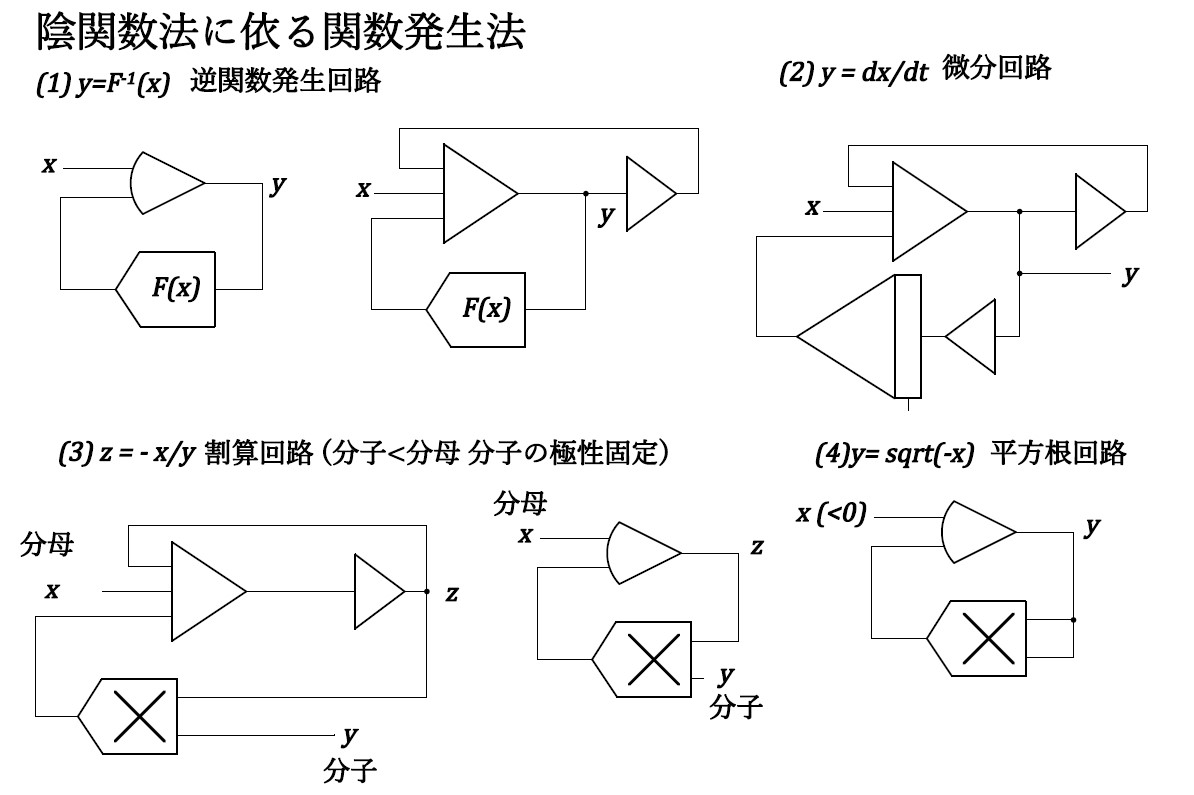
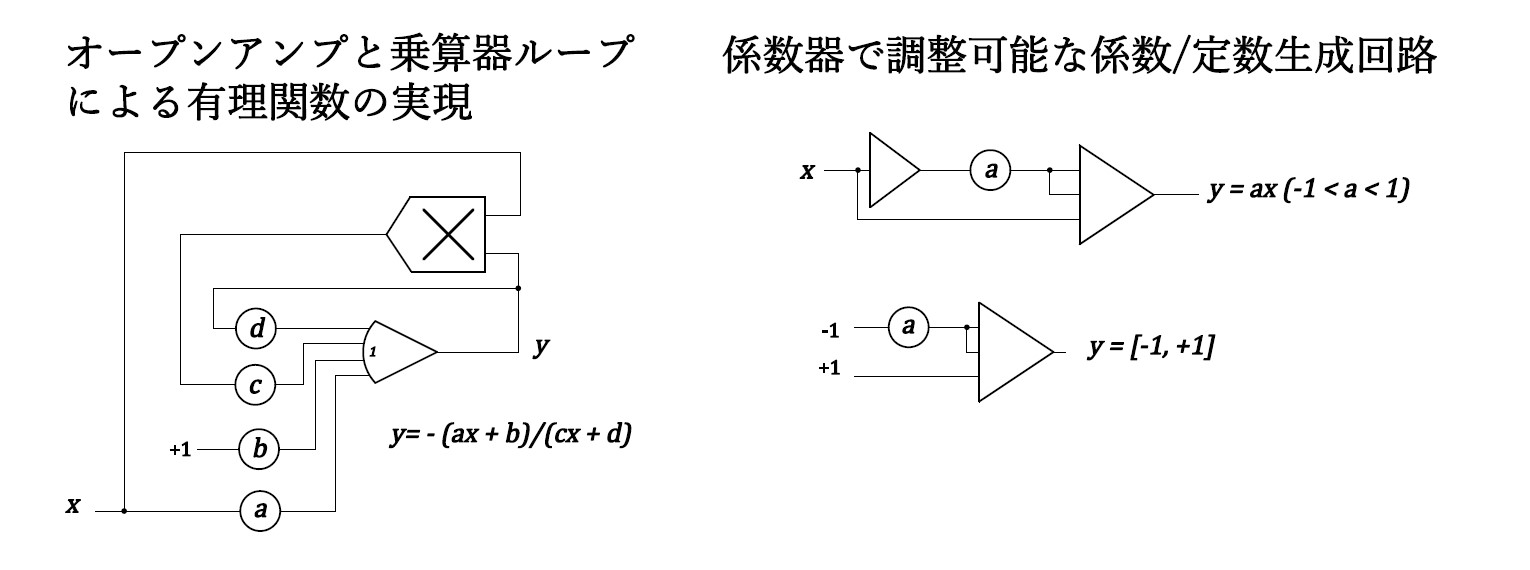
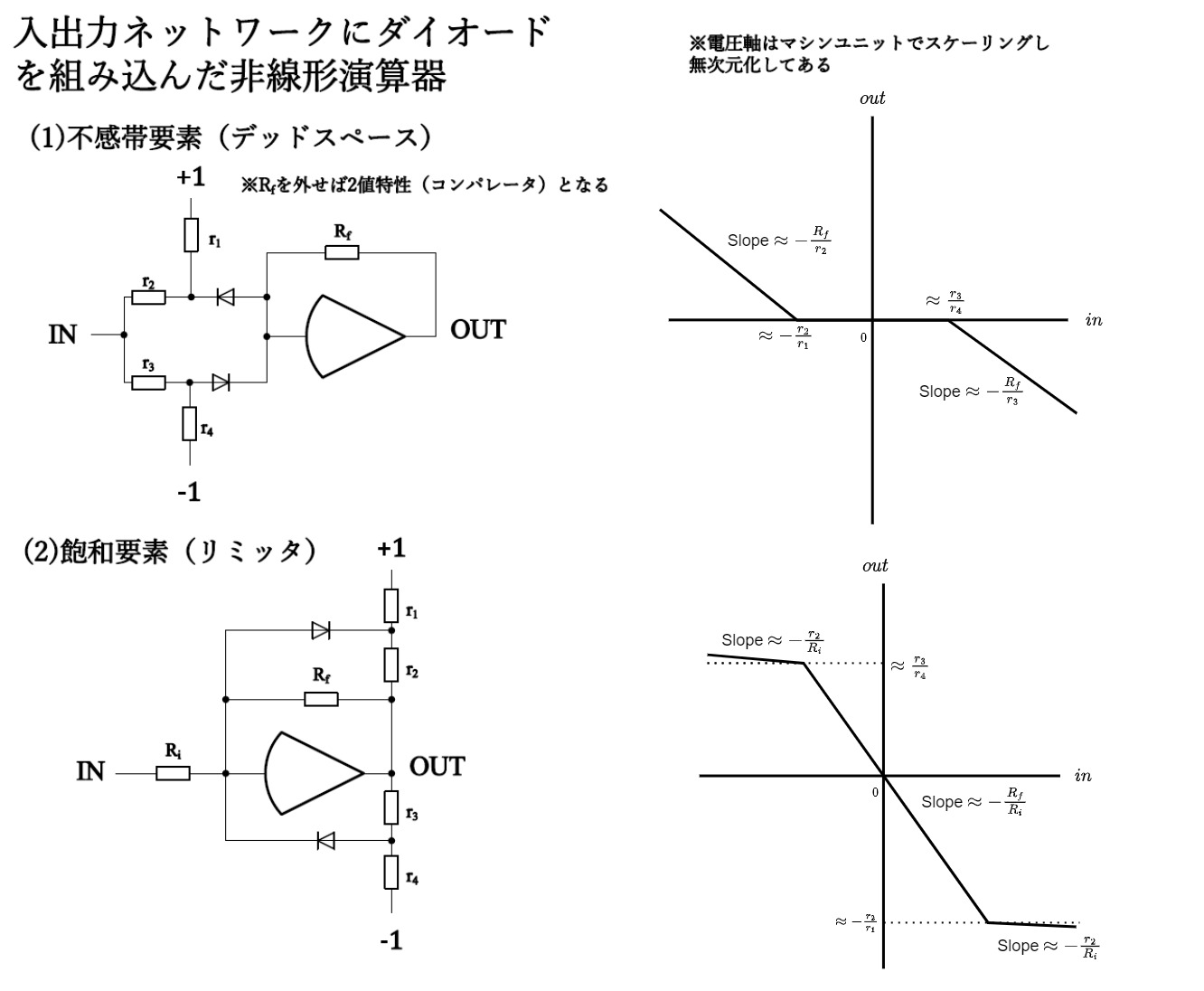
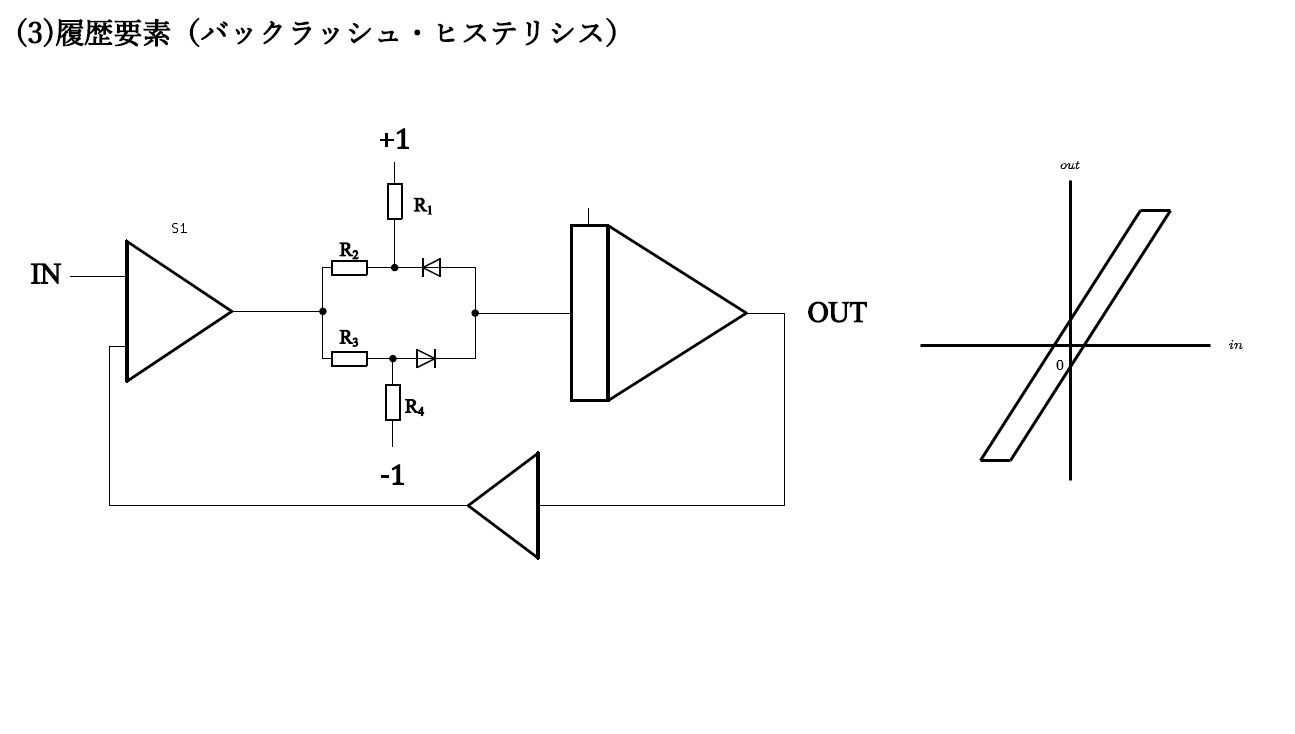
1.3 ダイオードを利用した非線形演算器

1.4 比較器を利用した非線形演算回路

 

1.5 座標変換・投影

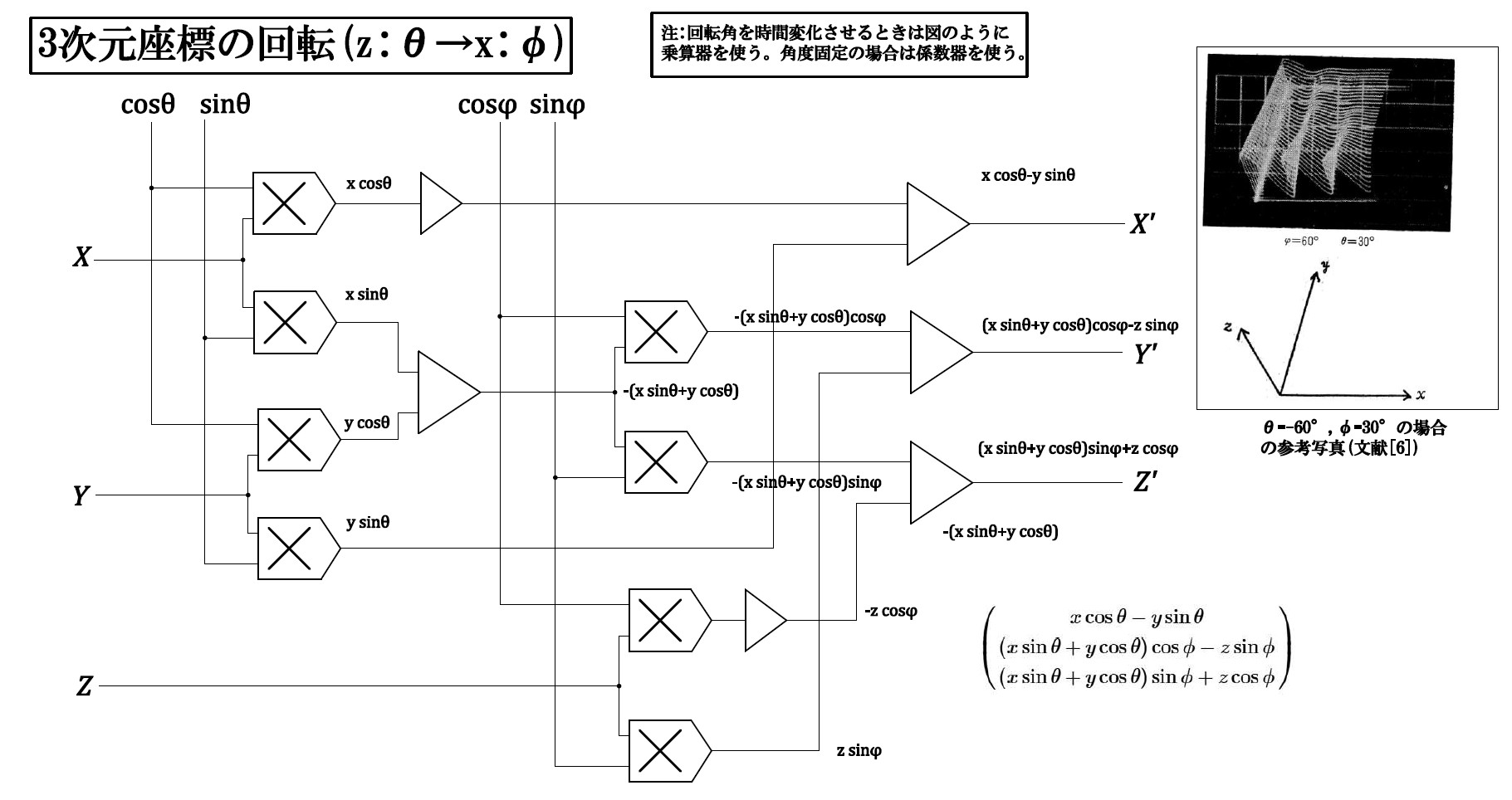
(1) z軸を中心に\(\theta\) 回転→x軸を中心に\(\phi\) 回転 (いずれも時計回りを正とする)

\begin{eqnarray} \left(\begin{array}{ccc} x'\\y'\\z'\end{array}\right)&=&\begin{pmatrix}1&0&0\\0&\cos{\phi}&-\sin{\phi}\\0&\sin{\phi}&\cos{\phi}\end{pmatrix}\begin{pmatrix}\cos{\theta}&-\sin{\theta}&0\\\sin{\theta}&\cos{\theta}&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}\\\\&=&\begin{pmatrix}x\cos{\theta}-y\sin{\theta}\\(x\sin{\theta}+y\cos{\theta})\cos{\phi}-z\sin{\phi}\\(x\sin{\theta}+y\cos{\theta})\sin{\phi}+z\cos{\phi}\end{pmatrix}\end{eqnarray}

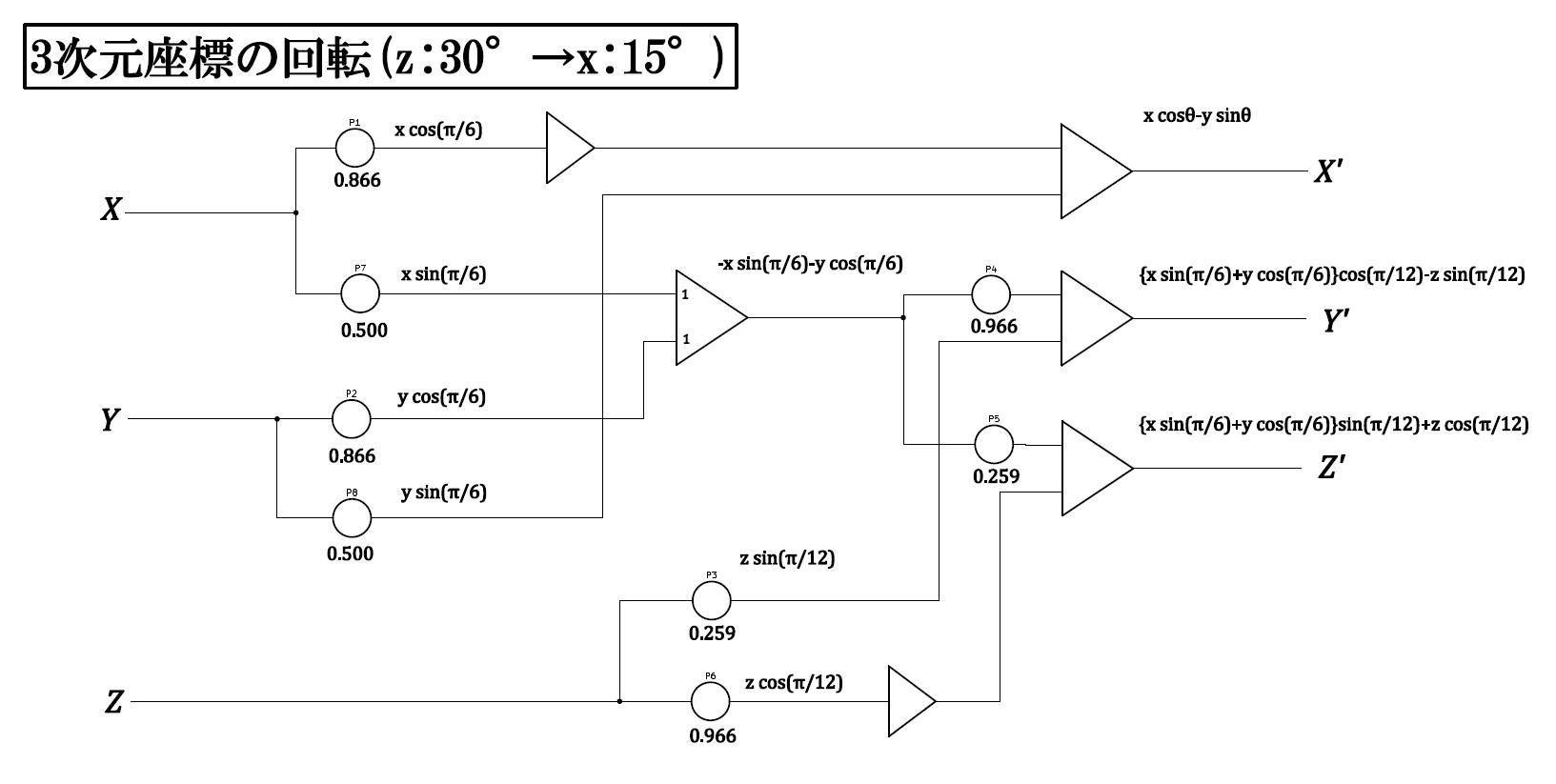
\(\theta=π/6\,,\phi=\phi/12\) で固定する場合は以下のような構成になる。パラメータを変化させて方程式の解を立体的に表示したい場合、この回路の\(x\)軸に独立変数、\(z\)軸に従属変数、\(y\)軸に可変パラメータを入力すると見通しの良い図が得られる。

 

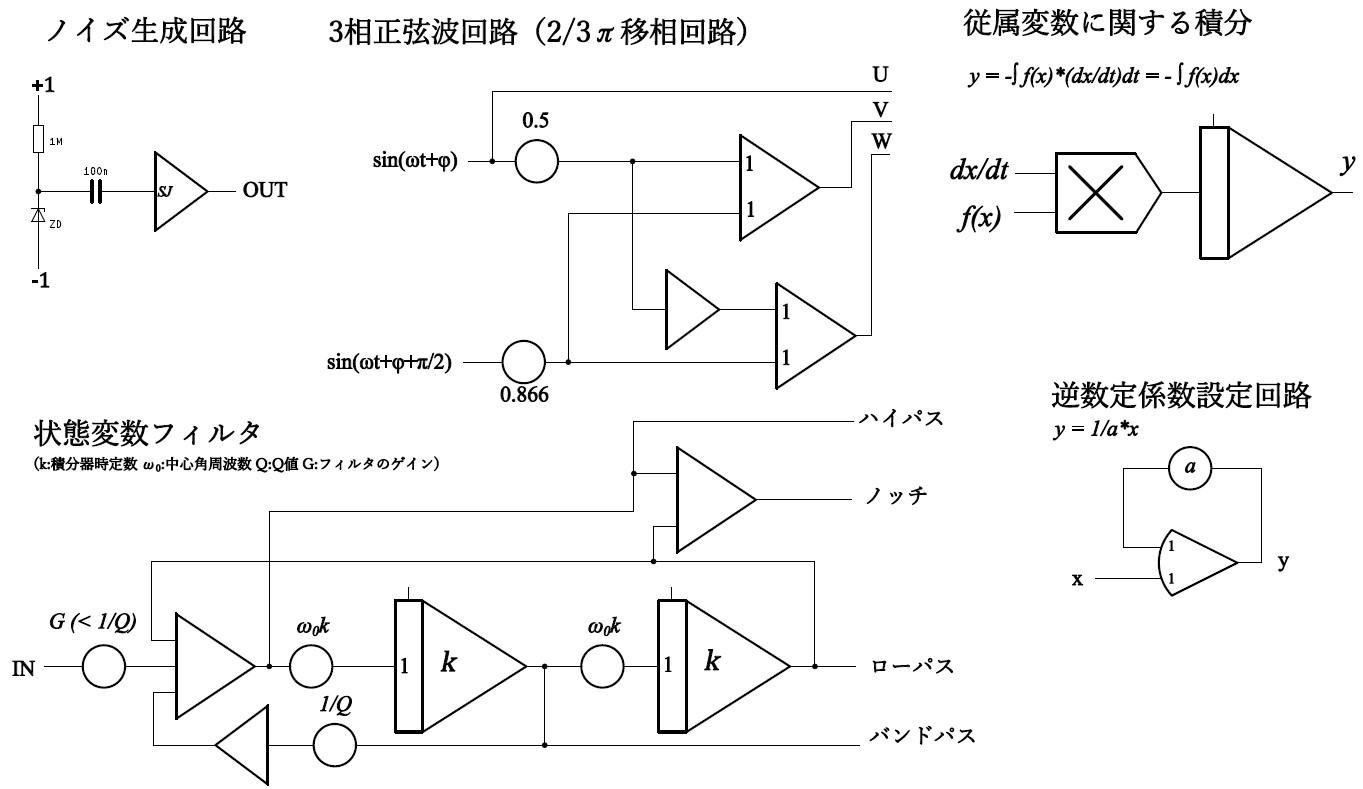
1.6 その他便利な回路

2.参考文献

[1] 野村民也, 三浦武雄. 「アナログ電子計算機」 コロナ社, 1960.

[2] 藤田広一. 「アナログ計算機のプログラム」昭晃堂,1978.

[3] 山下英夫. 「電子計算機 アナログ計算機編」オーム社, 1959.

[4] Michael Koch. " THAT Analog Computer Book Collection of Examples, useful Hints and Electronic Circuits "

http://www.astro-electronic.de/THAT_Analog_Computer_Book.pdf

[5] Granino A. korn & Theresa M. Korn. "Electronic Analog And Hybrid Computers"  McGraw-Hill Book Company, 1964. 

[6] 井上浩, 横田重雄.「アナログ電子計算機の3次元表示について」富山大学工学部紀要. (通号 20) 1969, p.20～32.

 

---

 

戻る