速度に比例する抵抗力が働く線形振動子
目次
2階線形常微分方程式はアナログコンピュータを使うまでもなく解析解が得られるのだが、ブロックダイヤグラム構成の基礎を把握する良い題材となるので、最初のアプリケーションとして選んだ。
1.準備
1.1 運動方程式
図1.1が今回の解析対象の「バネ-マス-ダンパ系」である。フックの法則にしたがうバネと速度に比例する抵抗力を生ずるダンパにより物体が支えられている(摩擦はないものとする)。適切なる初期条件を与えると、速度や変位が減衰的な振動を見せる。
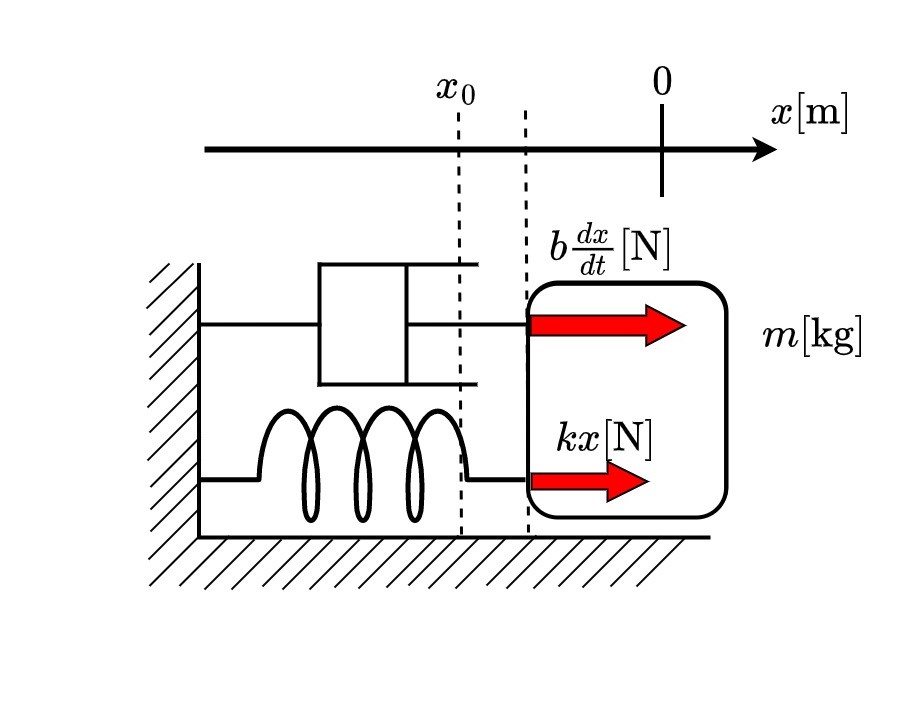
図1 バネ-マス-ダンパ系
運動方程式は
\[m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=-b\frac{\mathrm{d}x}{\mathrm{d}t}-kx \]
\[m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+b\frac{\mathrm{d}x}{\mathrm{d}t}+kx=0\tag{1} \]
ただし\(m\rm{[kg]}\)を質量、\(b\rm{[Ns/m=kg/s]}\)をダンパの粘性係数、\(k\rm[N/m=kg/s^2]\)をばね定数としている。無論これらは全て正の値であるとする。
工学上の解析で、よく方程式を無次元化することがある。一応、後述するアナログコンピュータ専用のスケーリング操作でその目的は達せられるため、冗長ではあるのだが、如何せん途中で出てくる固有角周波数や減衰比が重要なパラメータであるので一応触れておく。
位置変数\(x\rm{[m]}\)を、一定変位値\(x_a\rm{[m]}\)で規格化した無次元変数\(\tilde{x}=\frac{x}{x_a}\)を導入する。線形斉次微分方程式であるからそのまま
\[m\frac{\mathrm{d}^2\tilde{x}}{\mathrm{d}t^2}+b\frac{\mathrm{d}\tilde{x}}{\mathrm{d}t}+k\tilde{x}=0 \]
\[\frac{m}{k}\frac{\mathrm{d}^2\tilde{x}}{\mathrm{d}t^2}+\frac{b}{k}\frac{\mathrm{d}\tilde{x}}{\mathrm{d}t}+\tilde{x}=0\tag{2} \]
ただし式の次元が\(\rm{[s^{-2}]}\)となっていることに注意。
続いて時間について、固有非減衰角周波数\(\omega_n\rm{[rad/s]}\)を考える。これは減衰項が存在しない場合の角周波数、\(\sqrt{\frac{k}{m}}\)である。非減衰で1振動に要する時間は\(\frac{1}{\omega_n}\)となるから、これで時間\(t\)を正規化する。すなわち、\(\tilde{t}=\omega_n t=\sqrt{\frac{k}{m}} t\)。式(2)に\(t=\sqrt{\frac{m}{k}}\tilde{t}\)を代入して
\[\frac{\mathrm{d}^2\tilde{x}}{\mathrm{d}\tilde{t}^2}+\frac{b}{k}\sqrt{\frac{k}{m}}\frac{\mathrm{d}\tilde{x}}{\mathrm{d}\tilde{t}}+\tilde{x}=0\]
\[\frac{\mathrm{d}^2\tilde{x}}{\mathrm{d}\tilde{t}^2}+\frac{b}{\sqrt{mk}}\frac{\mathrm{d}\tilde{x}}{\mathrm{d}\tilde{t}}+\tilde{x}=0\tag{3} \]
(3)式の時点で式の次元は無次元となった。
ここで、1階微分の項の係数(無次元)
\[\frac{b}{\sqrt{mk}}=\frac{b}{k}\sqrt{\frac{k}{m}}=\frac{b}{k}\omega_n\]
を \(2\zeta\)とおく。つまり
\[\frac{b}{2\sqrt{mk}}=\frac{b}{2k}\sqrt{\frac{k}{m}}=\frac{b}{2k}\omega_n=\zeta\tag{4}\]
ここで\(\zeta\)を(臨界)減衰比という。
あえて\(2\zeta\)と置いた理由は、
\[\zeta=\frac{b}{2\sqrt{mk}}\tag{5}\]
とすることで、分子の\(b\)(ばねの減衰係数)と分母の\(2\sqrt{mk}\)との比として意味ある量にしたかったからである。分母の\(2\sqrt{mk}\)は臨界減衰係数といい、解析解の節で詳述するが、解が指数関数的減衰になるか振動的減衰になるかの「臨界」となる減衰係数を示す。減衰比は、臨界減衰係数\(2\sqrt{mk}\)と減衰係数\(b\)の比を示し、これが1より大であれば過減衰(指数関数的減衰)、小であれば振動減衰であることを示している。
減衰比\(\zeta\)を用いて式(3)を書き改めると
\[\frac{\mathrm{d}^2\tilde{x}}{\mathrm{d}\tilde{t}^2}+2\zeta\frac{\mathrm{d}\tilde{x}}{\mathrm{d}\tilde{t}}+\tilde{x}=0\tag{6} \]
これが無次元化した減衰振動方程式の表式である。物理的次元を持つ3つのパラメータが、ただ1つの無次元パラメータ\(\zeta\)のみに集約され、解析がしやすい形に変形できている。また、(4)式から
\[b/m = 2\zeta\omega_n\tag{7}\]
\[k/m={\omega_n}^2\tag{8}\]
であるから、力の次元をもつ元の運動方程式(1)の両辺を質量\(m\)で割った式は
\[\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+2\zeta\omega_n\frac{\mathrm{d}x}{\mathrm{d}t}+{\omega_n}^2x=0\tag{9} \]
と書き直せることもわかる。
1.2 解析解
(6)式の解析解を求める。対応する特性方程式は
\[s^2+2\zeta s+1=0\tag{10}\]
で、その根は
\[s=-\zeta\pm\sqrt{\zeta^2-1}\tag{11}\]
然らば一般解は
\[\tilde{x}(\tilde{t})=C_0 \exp{\{(-\zeta+\sqrt{\zeta^2-1})\tilde{t}\}}+C_1 \exp{\{(-\zeta+\sqrt{\zeta^2-1})\tilde{t}\}}\tag{12}\]
(\(C_0,C_1\)は初期条件に依る定数)
2階線形常微分方程式は、関数x(t)自身かその微分の線形結合が定数(ここでは0)になることを示している。厳密な説明ではないが、これから解がexpの形になることが自然だとわかるだろう。2階微分方程式なら2つの初期条件で特解が一意に定まる。
[1]\(\zeta>1\)のとき(特性根は全て実数)
一般解は
\begin{eqnarray}\tilde{x}(\tilde{t})&=&C_0 \exp{\{(-\zeta+\sqrt{\zeta^2-1})\tilde{t}\}}+C_1 \exp{\{(-\zeta-\sqrt{\zeta^2-1})\tilde{t}\}}\\ &=& \exp{(-\zeta\tilde{t})}(C_0\exp{\{(\sqrt{\zeta^2-1})\tilde{t}\}}+C_1\exp{\{(-\sqrt{\zeta^2-1})\tilde{t}\}})\tag{13}\end{eqnarray}
\(\zeta>\sqrt{\zeta^2-1}\)であるから、解は\(t\rightarrow\infty\)でつり合い位置\(x=0\)に指数関数的に収束する。
この状態が過減衰である。
[2]\(\zeta=1\)のとき(特性方程式は実重解を持つ)
2階微分方程式は2つの任意定数を含む一般解でないといけないが、特性根が1つの場合、不足する解空間を補完するため、重根のつくるexp関数のスカラー倍に加え、線形時間項をそれに乗じた関数のスカラー倍も考え、それらの和をとり、(14)式のようになる。任意定数を関数とみて定数変化法を用いれば導ける。
\begin{eqnarray}\tilde{x}(\tilde{t}) &=& \exp{(-\zeta\tilde{t})}(C_0+C_1\tilde{t})\tag{14}\end{eqnarray}
こちらも指数関数的に減衰するが、過減衰より収束するのが速い。
この状態が臨界減衰である。臨界減衰比\(\zeta=1\)なので、減衰定数\(b\)が臨界減衰定数\(2\sqrt{mk}\)と等しい。
[3]\(\zeta<1\)のとき(特性根は全て複素解)
一般解は
\begin{eqnarray}\tilde{x}(\tilde{t})&=&C_0 \exp{\{(-\zeta+j\sqrt{1-\zeta^2})\tilde{t}\}}+C_1 \exp{\{(-\zeta-j\sqrt{1-\zeta^2})\tilde{t}\}}\\ \\ &=& \exp{(-\zeta\tilde{t})}\left\{(C_0+C_1)\cos{(\sqrt{1-\zeta^2}\tilde{t})}+j(C_0-C_1)\sin{(\sqrt{1-\zeta^2})\tilde{t})}\right\}\\ &=& \exp{(-\zeta\tilde{t})}\left\{C_2\cos{(\sqrt{1-\zeta^2}\tilde{t})}+C_3\sin{(\sqrt{1-\zeta^2}\tilde{t})}\right\}\\ &=&\sqrt{C_2^2+C_3^2}\exp{(-\zeta\tilde{t})}\sin{\left(\sqrt{1-\zeta^2}\tilde{t}+\arctan{\frac{C_2}{C_3}}\right)} \tag{15}\end{eqnarray}
ただし、\(C_2=C_0+C_1,C_3=C_0-C_1\)は無次元定数。
振幅が指数関数的に減衰する正弦波となることが分かる。
図1.2に、\(\zeta\)が異なる値をとる時の解のグラフを示す。緑がζ=1、つまり臨界減衰解である。
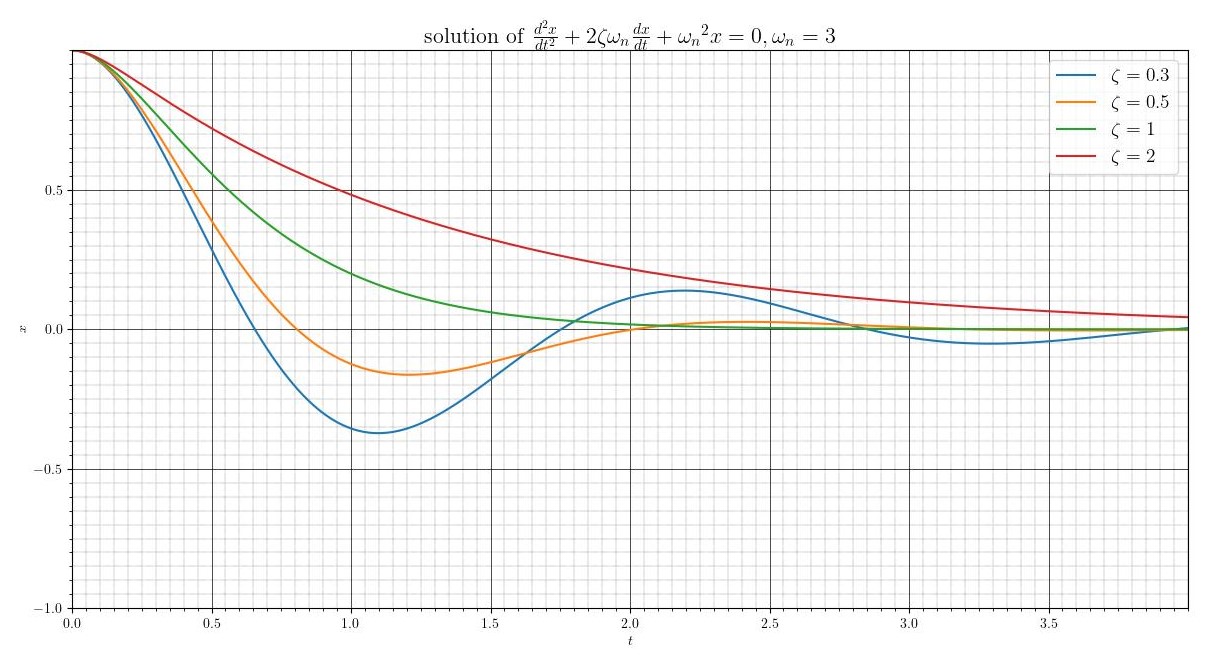
図2 減衰振動のデジタル計算機による解
さて、ここで無次元初期位置\(\tilde{x_0}\)、無次元初速度\(\tilde{v_0}=\frac{v_0}{\omega_n t}\equiv \tilde{\sigma}\)を初期条件とし、[3]\(\zeta<1\)の場合の特解を求めてみる。(15)式を微分すると速度の一般解が得られる。
\begin{eqnarray}\frac{\mathrm{d}\tilde{x}}{\mathrm{d}\tilde{t}}(\tilde{t}) &=& \sqrt{C_2^2+C_3^2}\exp{(-\zeta\tilde{t})}\left\{(-\zeta)\sin{\left(\sqrt{1-\zeta^2}\tilde{t}+\arctan{\frac{C_2}{C_3}}\right)} + \sqrt{1-\zeta^2}\cos{\left\{(\sqrt{1-\zeta^2}\tilde{t})+\arctan{(\frac{C_2}{C_3})}\right\}}\right]\\ &=& \sqrt{C_2^2+C_3^2}\exp{(-\zeta\tilde{t})}\sin{\left(\sqrt{1-\zeta^2}\tilde{t}+\arctan{\frac{C_2}{C_3}}+\arctan{\frac{\sqrt{1-\zeta^2}}{-\zeta}}\right)} \tag{16}\end{eqnarray}
(15),(16)式それぞれに\(\tilde{t}=0\)を代入する。
\begin{eqnarray}\tilde{x}(0)=\tilde{x_0}&=&\sqrt{C_2^2+C_3^2}\sin{\left(\arctan{\frac{C_2}{C_3}}\right)}\\&=&C_2\tag{17}\\ \frac{\mathrm{d}\tilde{x}}{\mathrm{d}\tilde{t}}(0)=\tilde{\sigma}&=&\sqrt{C_2^2+C_3^2}\sin{\left(\arctan{\frac{C_2}{C_3}}+\arctan{\frac{\sqrt{1-\zeta^2}}{-\zeta}}\right)}\\&=& \sqrt{C_2^2+C_3^2}\left\{\sin{\left(\arctan{\frac{C_2}{C_3}}\right)}\cos{\left(\arctan{\frac{\sqrt{1-\zeta^2}}{-\zeta}}\right)}+\cos{\left(\arctan{\frac{C_2}{C_3}}\right)}\sin{\left(\arctan{\frac{\sqrt{1-\zeta^2}}{-\zeta}}\right)}\right\}\\&=&\sqrt{C_2^2+C_3^2}\left(\frac{C_2}{\sqrt{C_2^2+C_3^2}}(-\zeta)+\frac{C_2}{\sqrt{C_2^2+C_3^2}}\sqrt{1-\zeta^2}\right)\\&=&-\zeta C_2 +\sqrt{1-\zeta^2}C_3\tag{18}\end{eqnarray}
よって、
\[C_2=\tilde{x_0} \tag{19}\]
\[C_3=\frac{\zeta \tilde{x_0}+\tilde{\sigma}}{\sqrt{1-\zeta^2}} \tag{20}\]
これらを一般解に代入して特解を得る。
\begin{eqnarray}\tilde{x}(\tilde{t}) &=&\sqrt{\tilde{x_0}^2 + \biggl( \frac{\tilde{\sigma}+\zeta\tilde{x_0}}{1-\zeta^2}\biggr)^{2}}\exp{(-\zeta\tilde{t})}\sin{\left(\sqrt{1-\zeta^2}\tilde{t}+\arctan{\frac{\tilde{x_0}\sqrt{1-\zeta^2}}{\tilde{\sigma}+\zeta\tilde{x_0}}}\right)} \tag{21} \\ \frac{\mathrm{d}\tilde{x}}{\mathrm{d}\tilde{t}}(\tilde{t}) &=&\sqrt{\tilde{x_0}^2 + \biggl( \frac{\tilde{\sigma}+\zeta\tilde{x_0}}{1-\zeta^2}\biggr)^{2}}\exp{(-\zeta\tilde{t})}\sin{\left(\sqrt{1-\zeta^2}\tilde{t}+\arctan{\frac{\tilde{x_0}\sqrt{1-\zeta^2}}{\tilde{\sigma}+\zeta\tilde{x_0}}+\arctan{\frac{\sqrt{1-\zeta^2}}{-\zeta}}}\right)} \tag{22}\end{eqnarray}
2.アナログコンピュータのプログラム
無次元の式(6)をアナログコンピュータで解析することにする。変数を置き換えて、
\[\frac{\mathrm{d}^2{x}}{\mathrm{d}{t}^2}+2\zeta\frac{\mathrm{d}{x}}{\mathrm{d}{t}}+{x}=0\tag{23} \]
非斉次線形であるので電圧換算は初期条件のみ行えばよいのだが、初期条件に任意性があるのなら最初から1にしておくとスケーリングが不要になる。ブロックダイヤグラムを次に示す。
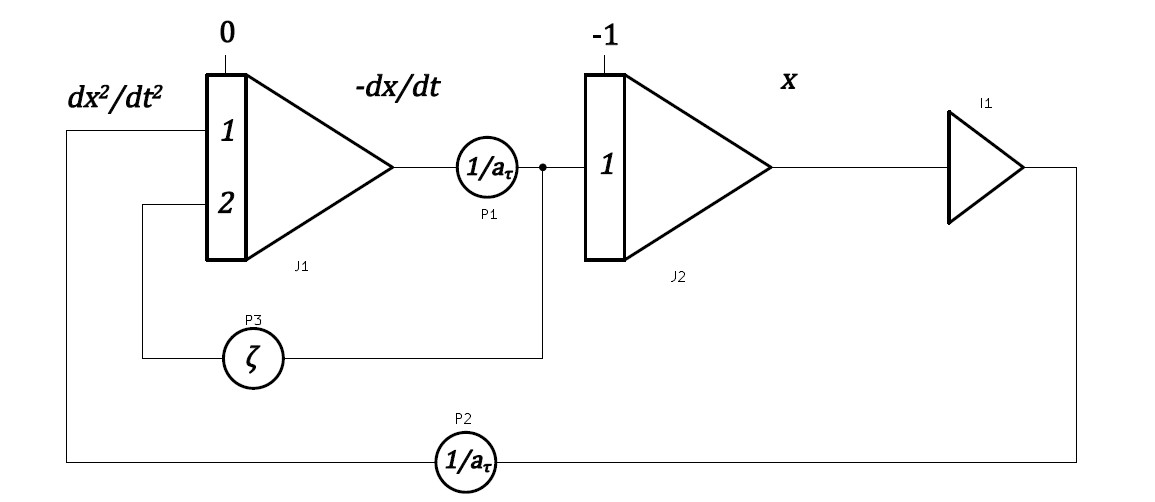
図3 減衰振動子のブロックダイヤグラム
時間換算係数の逆数\(1/a_{\tau}\)が非減衰角周波数\(\omega\)に等くなる。高速モードで\(a_{\tau}=10^{-3}\) とする場合は、積分器の時定数切り替えスイッチの操作のみで時間換算係数を設定できるので、係数器\(1/a_{\tau}\)は不要である。
3.結果
高速モードでアナログコンピュータを駆動し、解\(x(t)\)をアナログオシロスコープに出力させた。
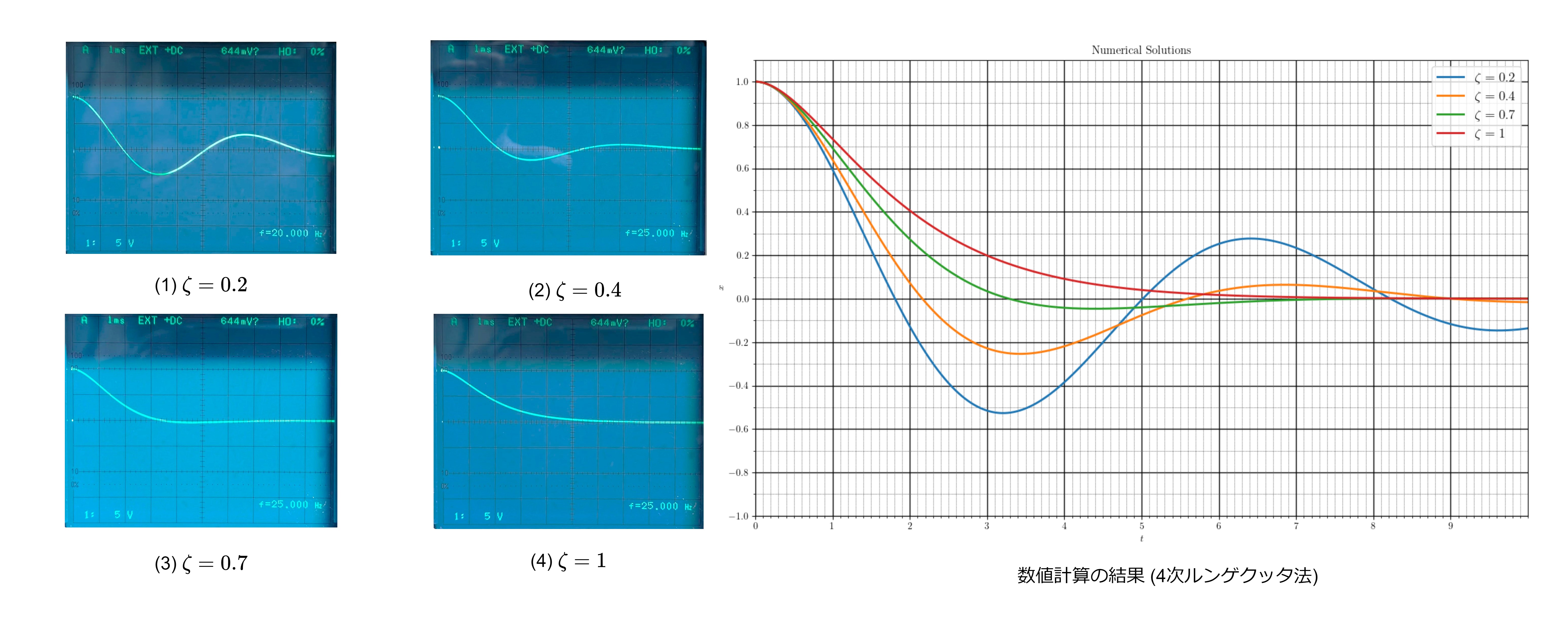
図4 \(x(t)\)のアナログコンピュータによる演算解
時間微分 \(\frac{\mathrm{d}x}{\mathrm{d}t}\)の解も一緒に表示させてみた。
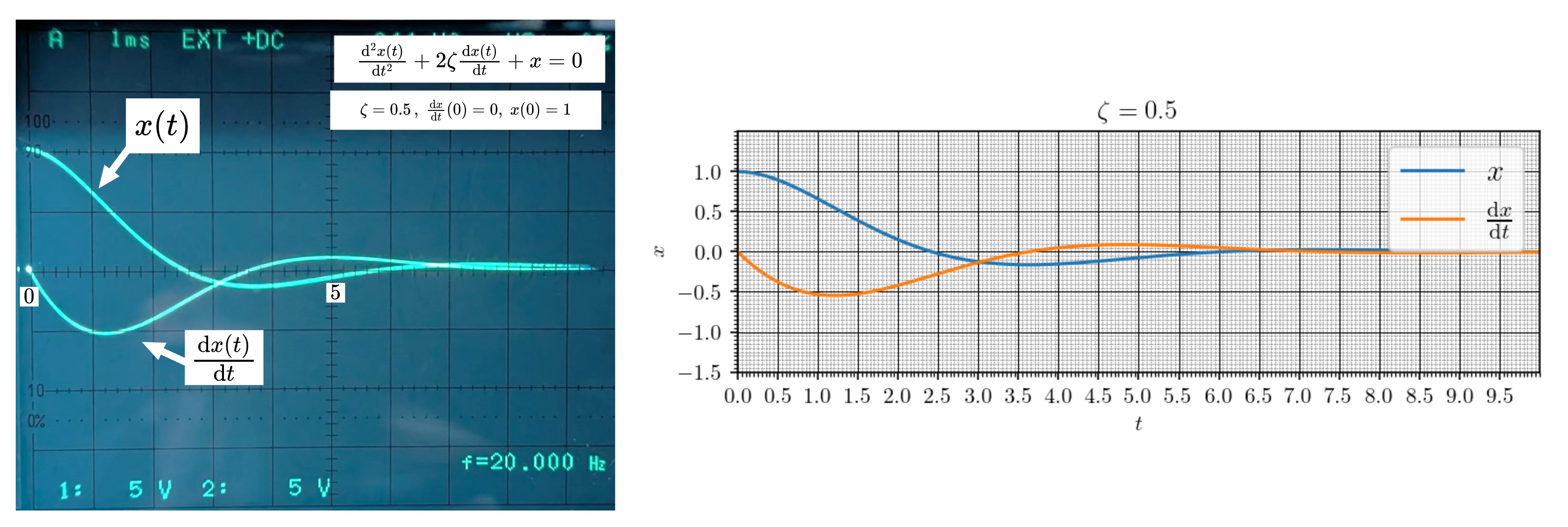
図5 \(x(t)\)と\(\mathrm{d}x/\mathrm{d}t\)のアナログコンピュータによる演算解
幾分精度面で不利である高速モードでの演算ではあるが、数値計算の結果(厳密解とみなしてよい)と十分に一致していることがわかる。
次に、アナログコンピュータを低速モードに設定し、\(\zeta=0.1\) から \(\zeta=1.0\) の場合のグラフをそれぞれペンレコーダで記録した。積分器の時間換算係数は1である。
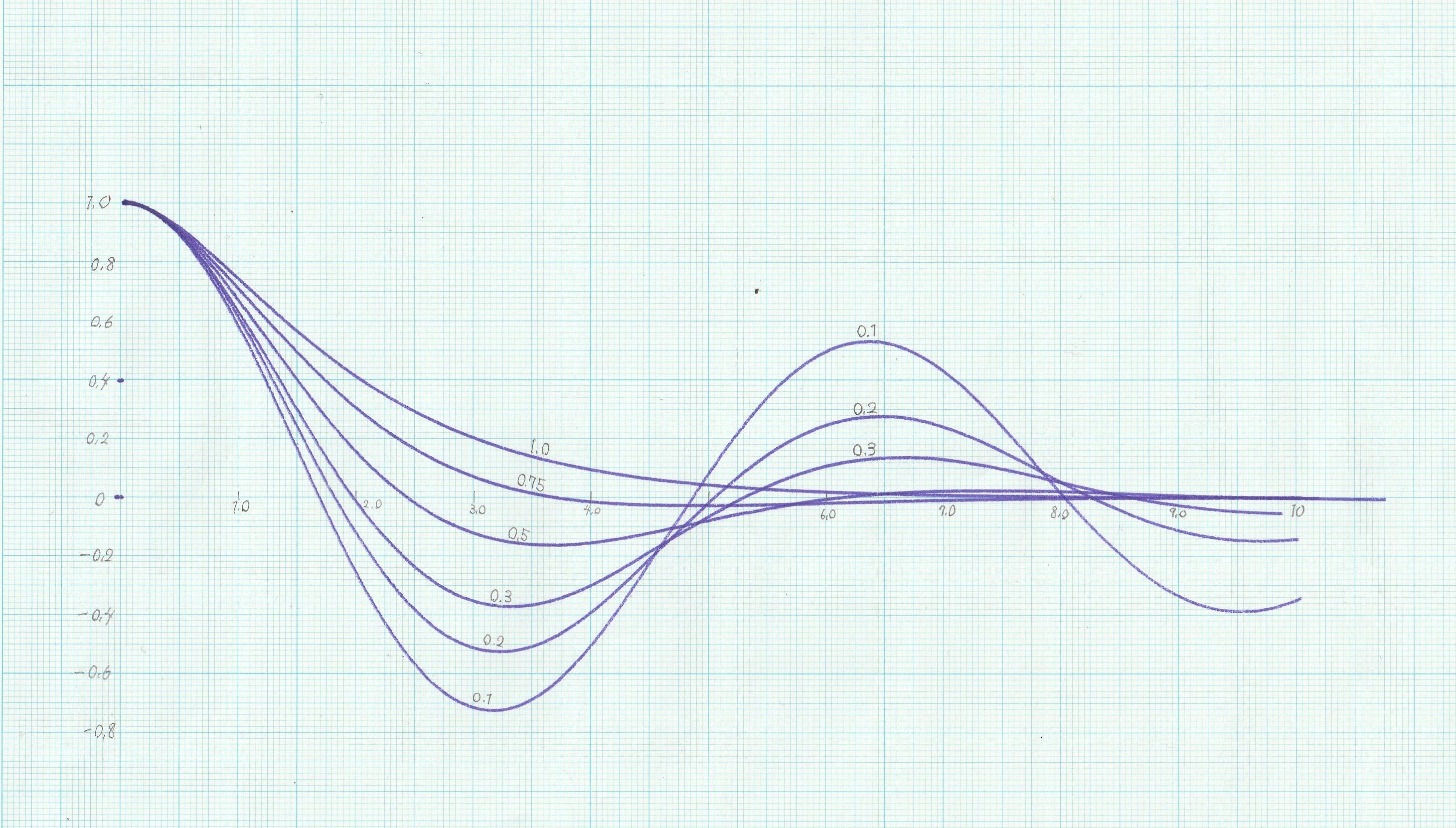
図6 低速モードによる解
こちらも厳密解とほぼ一致しており、実用性は十分である。
また、減衰比 \(\zeta\) の値を同期式十現象切替器(マルチプレクサ)により高速で切り替え、出力ベクトル\((t\,,\zeta\,,x(t))\)を回転行列のブロックダイヤグラムに通したのち、XYモードのオシロスコープに入力すれば、以下のような立体的俯瞰図が得られる。
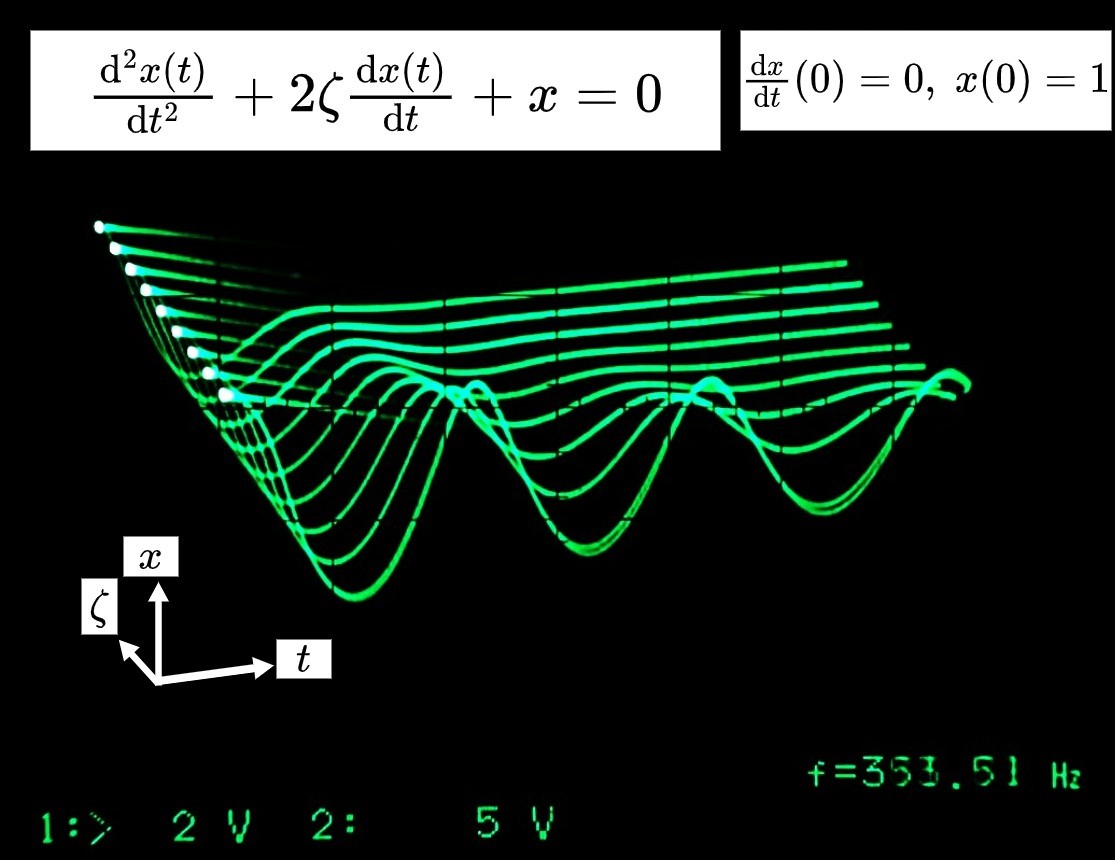
図7 パラメータ変化時の解関数群俯瞰図
回転行列回路は係数器で設定する場合、回転角は固定だが、乗算器を使えば回転角を時間依存関数とできるので、任意の方向を軸としてグルグル視点を変えるようなアニメーションを得ることも可能である。
複数パラメータでの演算解を安定して高速描写するためには、演算器制御信号とオシロスコープを同期させる必要があることはもちろん、被演算系積分器の時定数は通常の値である\(10^{-3}\)[s]では不足であり、最低でも\(10^{-4}\)[s]は必要であることに留意すべきである。そのような高周波演算では積分誤差(振幅減衰・振幅過大)が如実に表れるので、適宜微小フィードバックを掛けて補正するとよいだろう。
4.参考文献
[1] https://mechatronic-kame.hatenablog.jp/entry/2021/01/18/220754 (2025/3/2閲覧)