最急降下法による除算
目次
1.従来の手法
アナログ計算機における変数除算の方法として、陰関数法による実装が第1にあげられる。これは、オープンループアンプ(ゲインが負の無限大で近似できる演算増幅器)に乗算器ループを挿入する方法である。
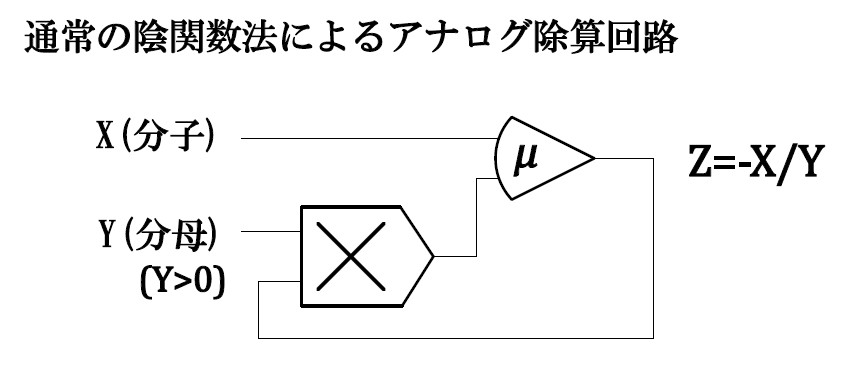
図1 従来の除算回路
増幅器及び乗算器の入力インピーダンスは非常に高いとみなせるので、
\begin{eqnarray}Z=-\mu\left(X+\,Z\,Y\right)\\\\Z\left(\frac{1}{\mu}+Y\right)=-X\end{eqnarray}
\(\mu\rightarrow{\infty}\) の極限をとると
\[Z=-\frac{X}{Y}\tag{1}\]
という関係が成り立つ。(無論、\(X,Y,Z\) は演算単位(乗算器のスケールファクタ)でスケーリングされた無次元計算機変数であり、電圧ではないことに注意。)
この回路は以下の欠点を有する。
- 分母が正の場合のみ動作する。(分母が負になるとポジティブフィードバックがかかることになり、出力は飽和して正常な解は得られない。)
- 分母が正であっても、分子が0に近い小さな値の場合、回路の帰還量が不足し安定動作しない。
要するに、基本的にこの回路は1象限除算器であり、分子の極性が変わらず正常動作範囲に収まることが分かっている箇所でしか使用できない。これは極めて不便である。例えば、0次ベッセル微分方程式
\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2}+\frac{1}{t}\frac{\mathrm{d}y}{\mathrm{d}t}+y=0\tag{2}\]
のような係数に極のある微分方程式を解く場合、時間原点(t=0)で除算器が正常動作しないため、まともに計算できない。高利得増幅器の入力側電流加算点を方程式の右辺の0とみなし、除算器を排したブロックダイヤグラムを組む手法は考案されている(詳しくはアプリケーション例「第1種ベッセル関数」を参照)が、使用乗算器としてサーボ乗算器を想定してある古い文献が元であるためか、乗算器ICを用いた演算では特異点での異常発振問題が解決できず、さらに回路の負帰還安定化が常に可能とも限らない。
2.最急降下法による安定な除算
前述の問題を解決するため、「最急降下法」を用いた演算が考案されている。(文献[1],[2])
最急降下法は、「演算の理論/2.6 最急降下法」の節で説明してあるように、微分方程式であろうと代数方程式であろうと、常に安定した演算回路を組むことが可能であり、広義の陰関数法とみなせる。アナログ最急降下法の理論の説明は上記ページを参考にして頂くとして、ここでは最急降下法の除算への応用に絞って解説する。
除算の式を変形すると、
\[x(t)-y(t)\,z(t)=0\tag{3}\]
となる。左辺を関数\(\varepsilon(t)\) として、その2乗\(\varepsilon^2(t)\)について1変数最急降下を行う。
\[\frac{\mathrm{d}}{\mathrm{d}t}\varepsilon^2(t)=2\varepsilon(t)\,\frac{\mathrm{d}\varepsilon(t)}{\mathrm{d}z(t)}\frac{\mathrm{d}z(t)}{\mathrm{d}t}\tag{4}\]
であるから、 \(\frac{\mathrm{d}z(t)}{\mathrm{d}t}\) を常に \(-2\,K\,\varepsilon(t)\,\frac{\mathrm{d}\varepsilon(t)}{\mathrm{d}t}\) と一致させればよい(\(K\)は正の定数)。すなわち、
\[\frac{\mathrm{d}z(t)}{\mathrm{d}t}=-2K\,\varepsilon(t)\frac{\mathrm{d}\varepsilon(t)}{\mathrm{d}z(t)}=2K\biggl\{x(t)-y(t)\,z(t)\biggr\}y(t)\tag{5}\]
という微分方程式をプログラムすればよろしい。演算回路は図2のようになる。
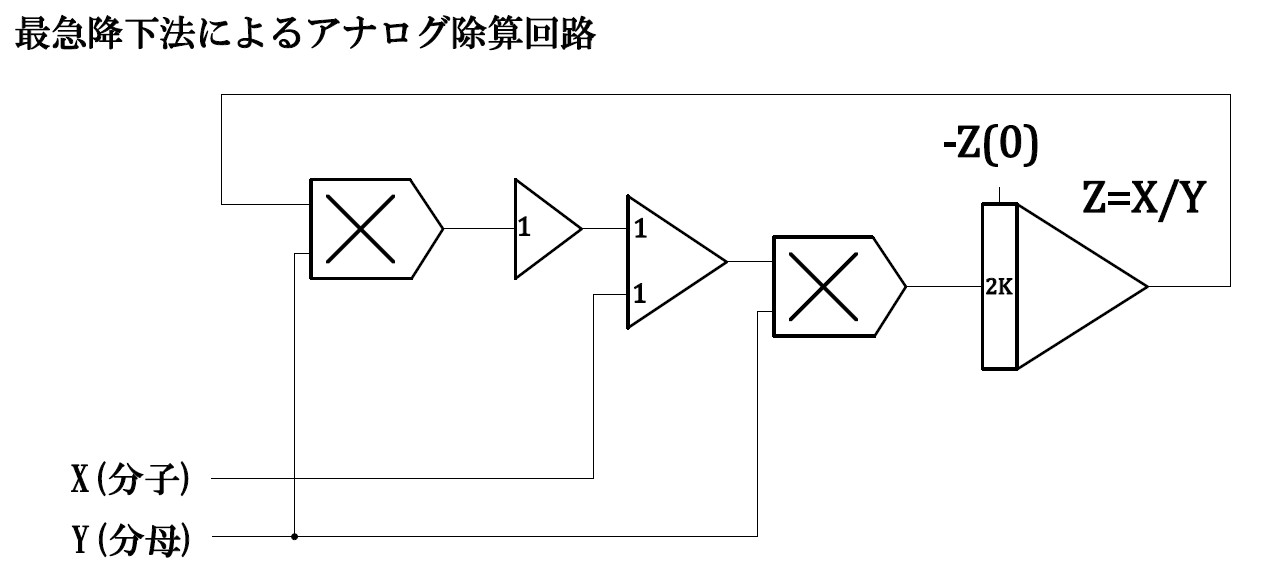
図2 最急降下法による除算回路
最急降下法は初期値の選び方が大切だが、割算の初期値は大抵の場合明らかであるため、最初からその値を積分器に与えれば定常値収束までの過渡誤差は抑えられる。
負の商 \(-x/y\) を得たいなら、\(\varepsilon(t)=x+yz\) と定めればよく、回路的には図2の反転器を除外することで実現させる。
方程式中に特異点の生じる除算(特に、独立変数が分母に来るようなもの)を安定に行えることが最大の利点といえる。
従来の手法と、最急降下法による除算の演算結果を実際に比較してみた。
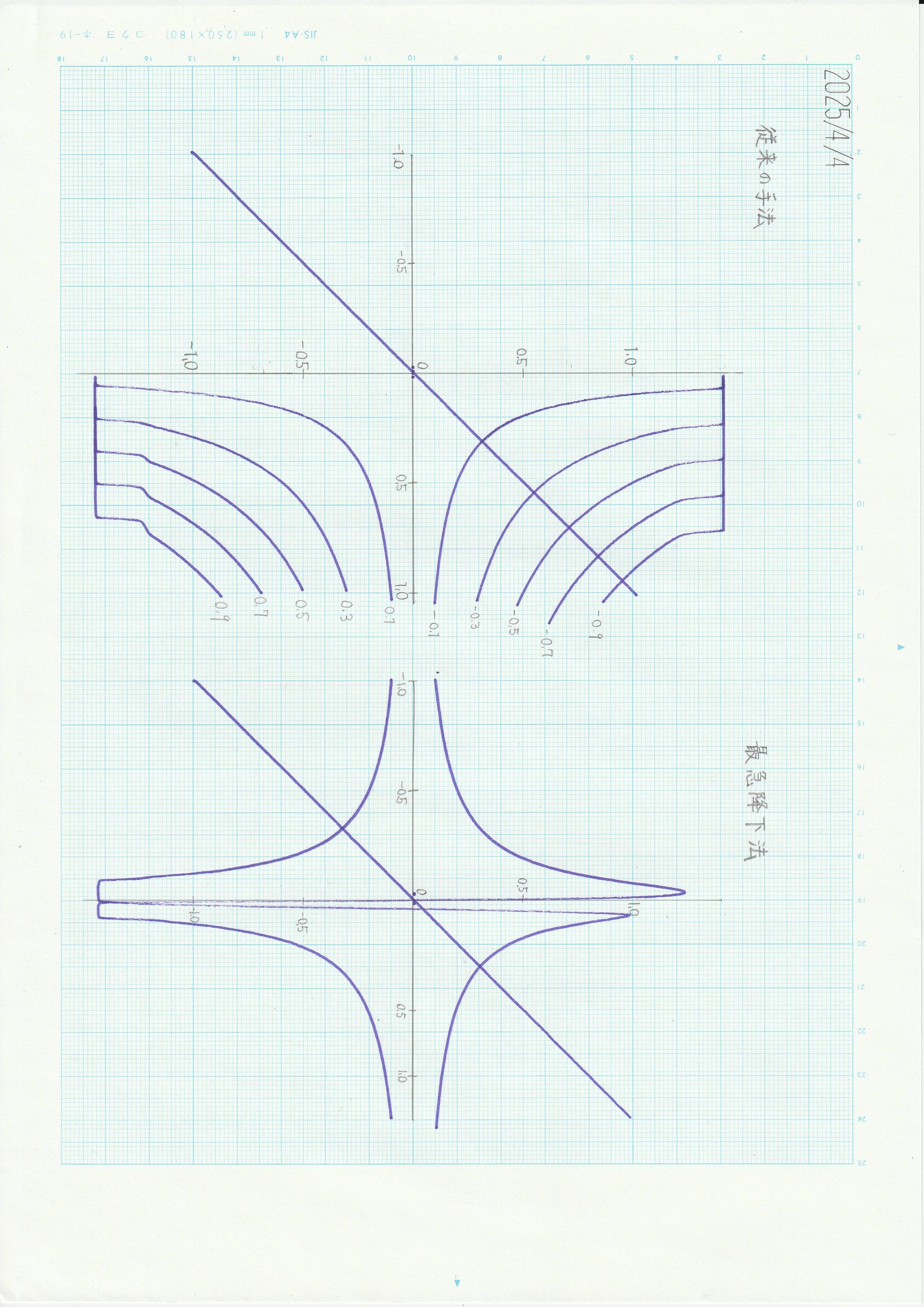
図3 除算の比較
左が従来の手法、右が最急降下法によるものである。両者ともに、分子の値を固定し分母に比例関数を入力して、解をペンレコーダに記録している。
最急降下法の第1象限が厳密解とずれているのは、ペンレコーダの掃引速度が速すぎて上手く追従できなかったためであり、適切な速度で掃引すれば、1MU以内であれば正しい解が得られる。
3. 誤差の評価
分母・分子ともに同周波数の正弦関数である場合の過渡誤差を解析的手段で評価してみる。
\[x(t)=A\sin{(\omega{t})}\,,\quad y(t)=B\sin{(\omega{t})}\tag{6}\]
(\(A\),\(B\)は正の定数)
\(z(t)\) についての1階線形微分方程式(5)の解析解は定数変化法により以下の如く求まる。
\[z(t)=\exp{\left(-\int{2K\,y(t)^{2}}\mathrm{d}t\right)}\left[\int\left\{{2K}x(t)y(t)\exp{\left(\int{2K\,y(t)^{2}}\mathrm{d}t\right)}\right\}\mathrm{d}t+C\right]\tag{7}\]
ただし\(C\)は積分定数である。
(7)式に(6)を代入すると、
\begin{eqnarray}z(t)&=&\exp{\left(-\int{2KB^{2}\sin^{2}{(\omega{t})}}\mathrm{d}t\right)}\left[A\int\left\{{2K}B\sin^{2}{(\omega{t})}\exp{\left(\int{2KB^{2}\sin^{2}{(\omega{t})}}\mathrm{d}t\right)}\right\}\mathrm{d}t+C\right]\tag{8}\end{eqnarray}
ここで
\[\mathrm{d}w(t)={2K}B^{2}\sin^{2}{(\omega{t})}\exp{\left(\int{2KB^{2}\sin^{2}{(\omega{t})}}\mathrm{d}t\right)}\mathrm{d}t\tag{9}\]
つまり
\[w(t)=\exp{\left(\int{2KB^{2}\sin^{2}{(\omega{t})}}\mathrm{d}t\right)}\tag{10}\]
とおくと、(8)式は
\begin{eqnarray}z(t)&=&\frac{1}{w(t)}\left(\int{\frac{A}{B}\mathrm{d}w+C}\right)\\\\&=&\frac{A}{B}+\frac{C}{w(t)}\\\\&=&\frac{A}{B}+C\,\exp{\left(-\int{2KB^{2}\sin^{2}{(\omega{t})}}\mathrm{d}t\right)}\\\\&=&\frac{A}{B}+C\,\exp{\left(-KB^2\,t+\frac{KB^2}{2\omega}\sin{(2\omega{t})}\right)}\tag{11}\end{eqnarray}
(11)が微分方程式の一般解である。
初期条件として \(t=0\) のとき \(z(t)=0\) が与えられるから、\(C=-A/B\)。ゆえに特解は
\begin{eqnarray}z(t)&=&\frac{A}{B}\left\{1-\exp{\left(-KB^2\,t+\frac{KB^2}{2\omega}\sin{(2\omega{t})}\right)}\right\}\\\\&=&\frac{A}{B}\left\{1-\left(e^{-KB^2\,t}\right)\left(e^{\frac{KB^2}{2\omega}\sin{(2\omega{t})}}\right)\right\}\tag{12}\end{eqnarray}
と求まる。\(\displaystyle{e^{-KB^2\,t}}\) の項が過渡誤差となり、\(\displaystyle{e^{\frac{KB^2}{2\omega}\sin{(2\omega{t})}}}\) の項が振動誤差となっているので、入力周波数の2倍で振動しながら指数関数的に定常値へ収束することがわかる。もちろん収束先は
\[z(t)\rightarrow{\frac{A}{B}}\tag{13}\]
である。
以上のことから、
- \(KB^2\) の値が大きい程はやく定常値に収束する
- 入力信号の角周波数\(\omega\) が大きく、\(KB^2\) の値が小さい程、振動誤差が小さくなる
が言える。積分器ゲイン\(2K\)を大きくすればより素早く真の解へ収束するが、その代わり振動誤差が大きく出るので、大きすぎるのも良くない。ちょうどいい値を探る必要がある。
実際には適切な初期値を与えれば上記1は無視できるので、最適な\(K\)の値というのは低速モードにおいては比較的簡単に見つかるだろう。
高速モードでは、最適なゲインを得るためには積分器のゲインをかなり大きく(時定数をかなり小さく)する必要がある。場合によっては、積分器のかわりにオープンループアンプを用いるとよいかもしれない。
低速モードにおいて、最急降下法を用いて \(\sin{(\omega{t})}/\sin{(\omega{t})}\) を演算した結果を図4に示す。
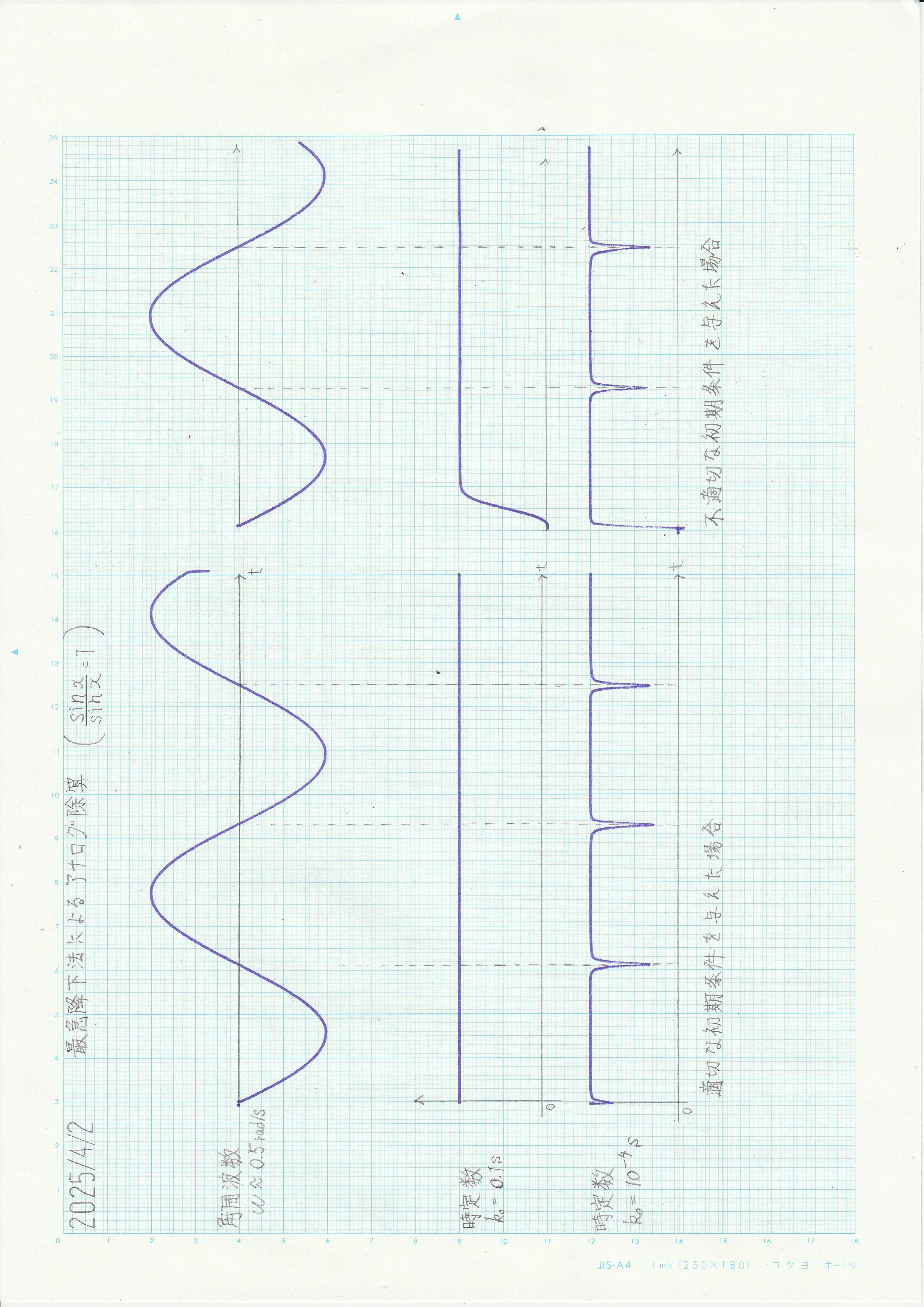
図4 最急降下法による\(\sin{(\omega{t})}/\sin{(\omega{t})=1}\) の解
左は正しい初期値1.0を与えた場合、右は不適切な初期値0を与えた場合の演算結果である。ゲインが大きい(時定数が小さい)と収束までの時間は短くなっているが、入力信号値が0に近い箇所で振動項に起因する誤差が生じている。
入力信号角周波数 \(\omega=0.5\)rad/s に比較して適度な大きさの時定数をもつ積分器を選択し、初期値をきちんと与えれば、これらの誤差はほぼ無視できるようになる。
4.正接関数
\(\tan(t)=\sin(t)/\cos(t)\) の演算解を図に示す。
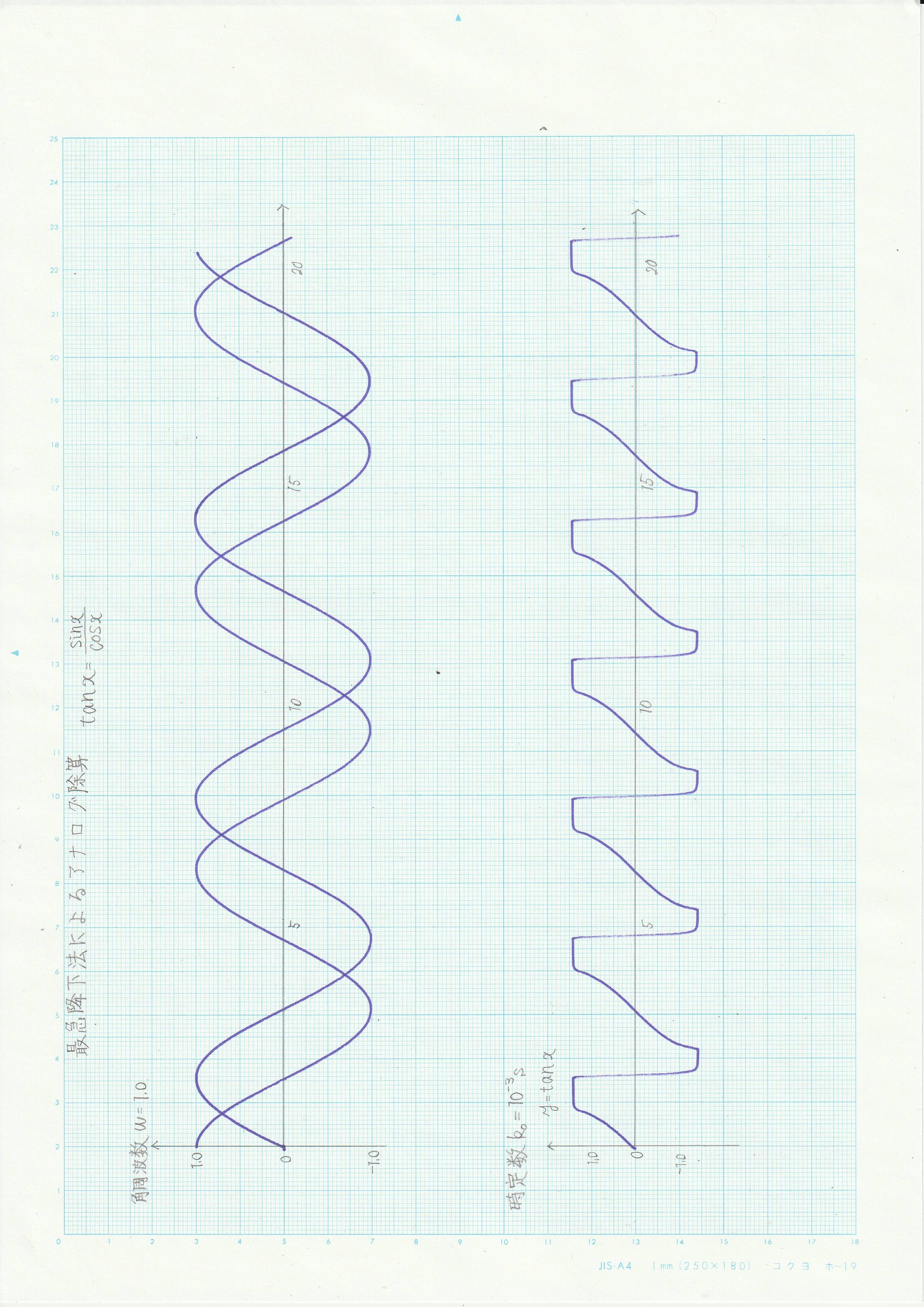
図4 tanの解
これは2入力振幅を相等しくした場合の結果である。振幅比を調整すれば、任意の倍率にスケーリングできることに留意して欲しい。
5.分母に\(t\)等がある場合
\[z(t)=\frac{x(t)}{y(t)}=\frac{\sin{t}}{t}\tag{14}\]
のような関数(Sinc関数)や、第1種ベッセル関数求解回路中の除算など、
(1) \(t=0\)において分母分子 の値がともに0であるが、数学的に有限の初期値が存在し、
(2) 分母の値がすぐには大きくならない
ような形の除算を行う場合、図2に示したような回路ではオーバースケール・低周波発振してしまい、ちょうどよいゲインを探すことは非常に難しくなる。そのような場合で大切なのは、できるだけ最急降下法回路のループゲインKYを大きくすることと、スケーリングをしっかり行うことの2点である。
図2の回路の加算器をオープンループアンプとして、フィードバックに係数器を挿入し値1/Kを設定すると、オープンループアンプ回路のゲインはKとなる。係数器で設定できる値の範囲は \(0\leq{1/K}\leq{1}\) であるから、ゲインKとして非常に大きな値を選ぶことができる。積分器入力端子を入れ替えたり、コンデンサを入れ替えたりするよりも手間を掛けずに最適なKを見つけることができる。また、分母の値がすぐには大きくならないので、分子の電圧換算係数を小さく選ぶ(分子をダウンスケールする)ことも必要である。
以下はsinc関数のグラフを最急降下法除算によりえがいたものである。Z(t)×Y(t)の積を計算する乗算器の出力(分子X(t)=\(\sin(t)\)に漸近)も併記している。
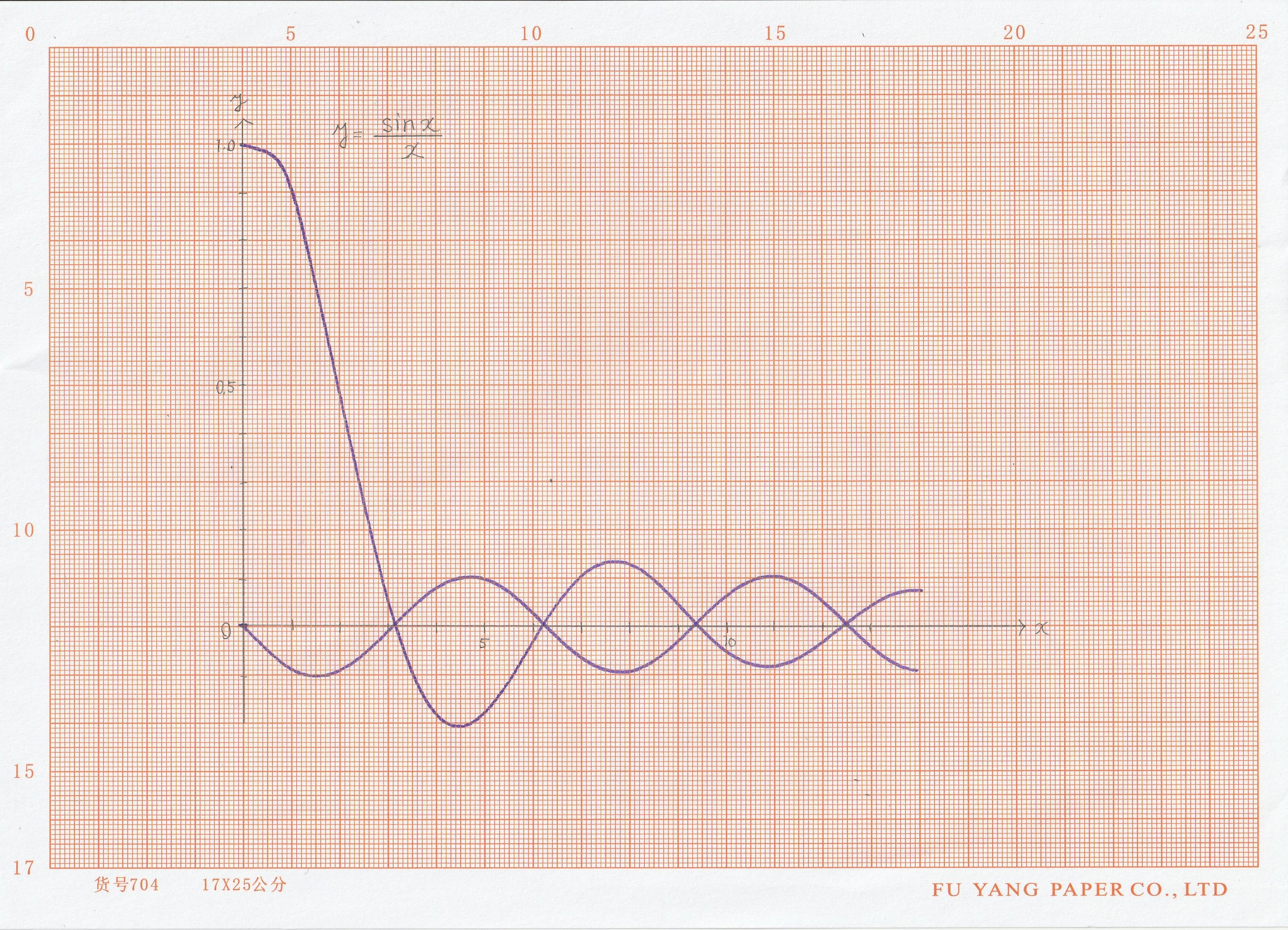
図5 sinc関数の解
6.参考文献
[1] 藤田広一, 山田安幸, 梅村護. 「最急降下法を利用した割算及び相関の演算法」アナログ技術研究会資料, 9巻, 5号, p15-p27, 1969.
[2] 藤田広一. 「アナログ計算機のプログラム」昭晃堂,p98-p99, 1978.
[3] Granino A. korn & Theresa M. Korn. Electronic Analog And Hybrid Computers. McGraw-Hill Book Company, 1964.