演算の理論
アナログコンピュータの実際の運用に必要不可欠な知識
目次
※以後、アナログコンピュータまたはアナログ計算機の語を使用する場合、特記無い限り「電子式アナログ計算機(間接相似型)」を指すものとします。
1. アナログコンピュータの演算要素
本章ではアナログコンピュータの演算要素について紹介する。以下が主な演算要素のリストである。
- 積分器
- 加算器
- 反転器
- 係数器
- 乗算器
電子式アナログ計算機では、これらの要素同士をパッチパネル上で結線して、解を電圧波形として得る。なかでも微分方程式を扱うことがアナログコンピュータの主目的であるため、積分器は特に重要である。上記以外にもアナログコンピュータの演算要素や補助要素が多く存在するが、ここでは上記の基本的な演算器に限って説明する。
1.1 積分器
この要素はオペアンプ・抵抗・コンデンサで構成された積分回路に他ならない。実際の計算機の積分器はこれほど単純な回路ではない。微分方程式を解くことが積分器の存在意義であるが、一般に\(n\)階の常微分方程式の解には\(n\)個の任意定数が含まれている。つまり、各積分器毎に任意の初期条件を設定できるような回路でないといけないのだ。その初期条件設定機能を付加した積分器の記号は以下のようになる。出力電圧と初期値電圧、入力電圧の関係式も図の通り。
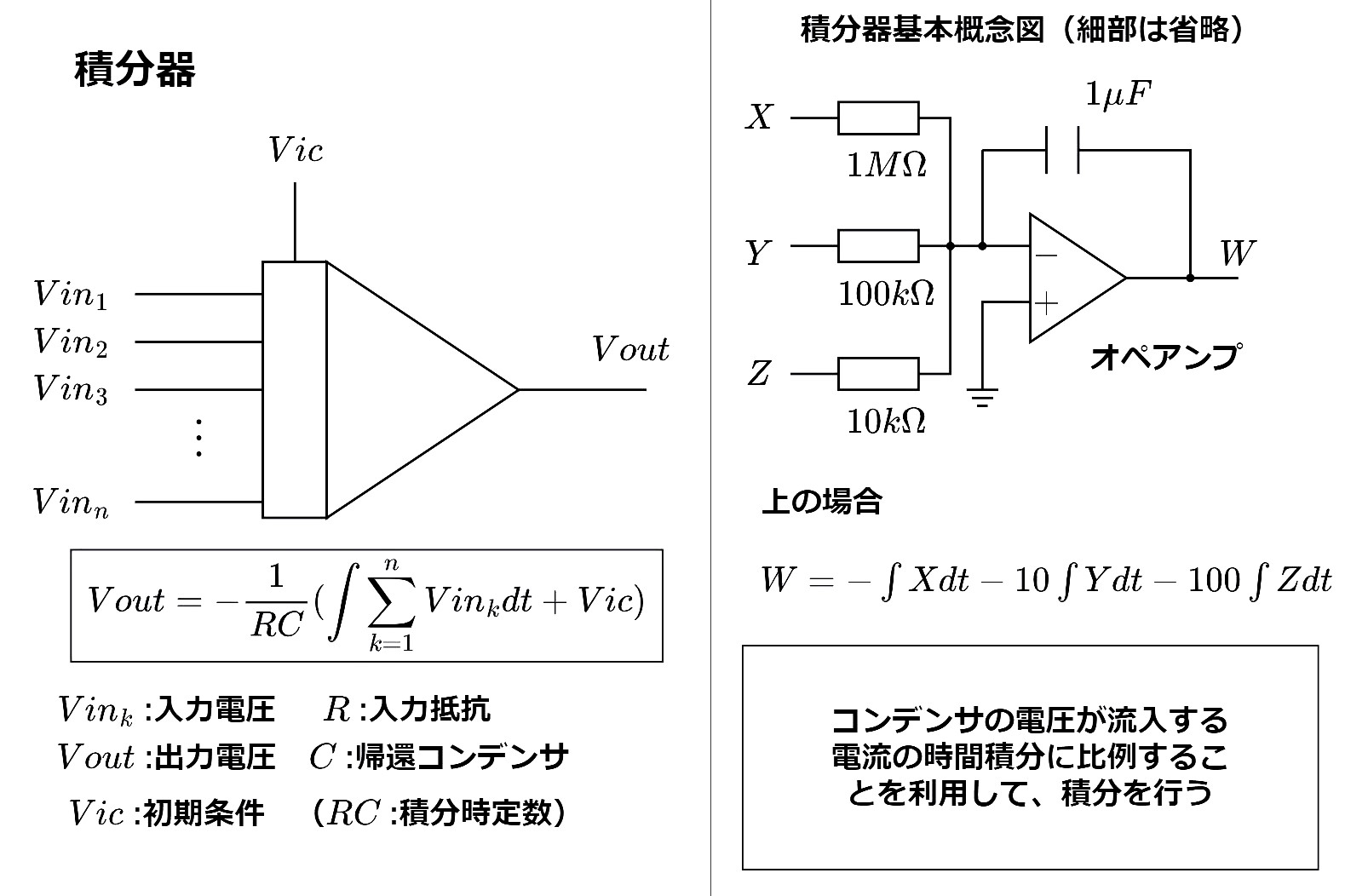
(右半分の概念図では簡単のため初期条件設定部分は省略してある。)
出力の符号が反転していることに注意されたい。初期条件電圧\(V_{ic}\)にもその符号がかかることに注意。すなわち、初期条件端子に入力する電圧値の符号は、設定したい初期条件の符号の反対になる。
直接相似型のアナログコンピュータは「低速型」と「高速(繰り返し)型」に分かれる。低速型は、時定数が\(RC=1\)sに近い値で演算を行い、解波形が角周波数成分1rad/s~10rad/s程度でペンレコーダなどに描きだされる(実時間動作ともいう)。高速型は数キロヘルツから数百ヘルツ程度の速さで繰り返し演算を行えるように積分器の時定数が小さくしてある。演算の繰り返し周波数がある程度高ければ、オシロの水平掃引と同期させることで波形が画面にちらつくことなく静止表示できる。これが高速動作である。一般にアナログコンピュータの演算器のなかで時間に関する演算を行うのは積分器のみであるため、積分器の時定数が系の各信号の周波数を決定すると言える。コンデンサ容量を切り替えることで時定数を1s(~0.1s)と(100ms~)1msとで切り替えられる「低速・高速両用」アナログコンピュータも存在した。
上図の積分器記号において入力端子側長方形に書かれた数字はいずれもその入力端子のゲインを表す。低速型の場合、例えばフィードバックコンデンサが1μFで入力端子が1MΩの場合ゲイン\(\frac{1}{RC}=1\) /sになり、100kΩの場合、ゲイン\(\frac{1}{RC}=10\) /sと計算できる。高速型の場合注意が必要で、フィードバックコンデンサが1nF=\(10^{-3}\)μF等の容量になるが、この\(10^{-3}\)は時間換算係数に相当する(後に詳述)ので無視する。すなわち高速型では1nFと1MΩの組み合わせでゲイン1とする。
当然のことだが、高速動作では初期状態・演算状態の切り替えを手動スイッチでちんたらやっているひまはない。かつてのアナログコンピュータは、コントロールユニットのスイッチや制御回路からのパルス信号(多くの専門書ではこのデジタル信号および信号線に\(\phi\)と名付けている。本稿でもこの慣習に従う)を受けたリードスイッチ・電子管スイッチ・FETスイッチ等によって、初期状態⇔演算状態の切り替えを高速に繰り返した。無論周波数が高くなれば誤差が大きくなり、精度が低速型と比較して幾分か落ちてしまうが、高速型は解波形が常に画面上で走査更新されているため、係数ポテンショメーターで方程式のパラメータを変化させつつ、それに伴う解の形状変化の様子を同時に調べるといった芸当が可能であり、大変便利であった。低速型の場合はこうはいかない。低速演算中にパラメーターを変えれば得られた解が何の意味もなさなくなるからである。以下が高速繰り返し形の演算の概要を示した図である。
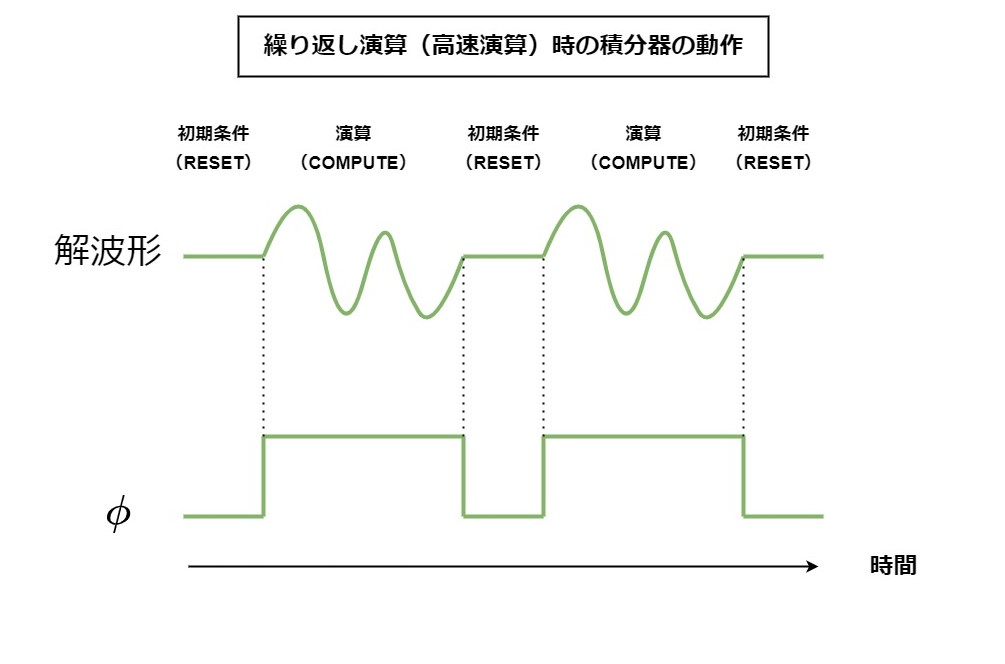
また、初期状態(REST/IC)・演算状態(OPERATE/COMPUTE)の他に、「保持(HOLD)」という状態を設ける計算機もある。以下がHOLD動作の概念図である。
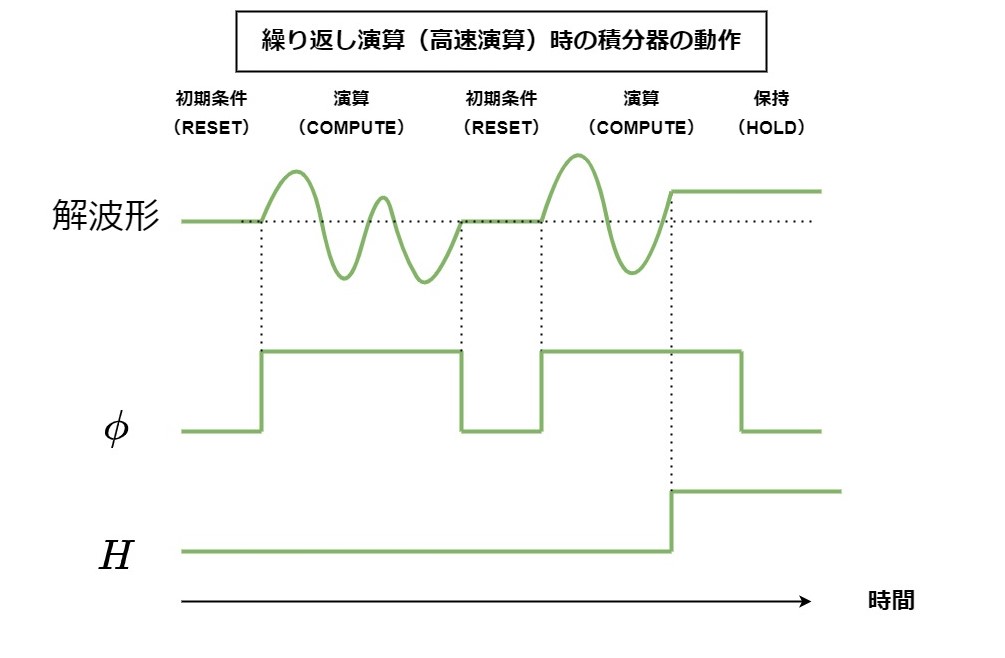
これは、信号線\(H\)がHighになった時点での積分器出力を保持している状態である。\(H\)がHighのとき、信号線\(\phi\)の電圧の如何にかかわらずコンデンサ側が積分回路から切り離され、その時点での電圧を維持する。ただし、実際のコンデンサは漏れ電流などの誤差により電荷が次第に放出され、長時間この状態のままだと電位は減衰していく。減衰の程度コンデンサの種類と性能による。
保持の機能は電子式アナログ計算機に記憶の機能を持たせることができるなどいろいろと便利である。
これらの動作を踏まえ、初期条件・演算・保持の各状態を考慮した、より詳細な積分器の回路を以下に示す。
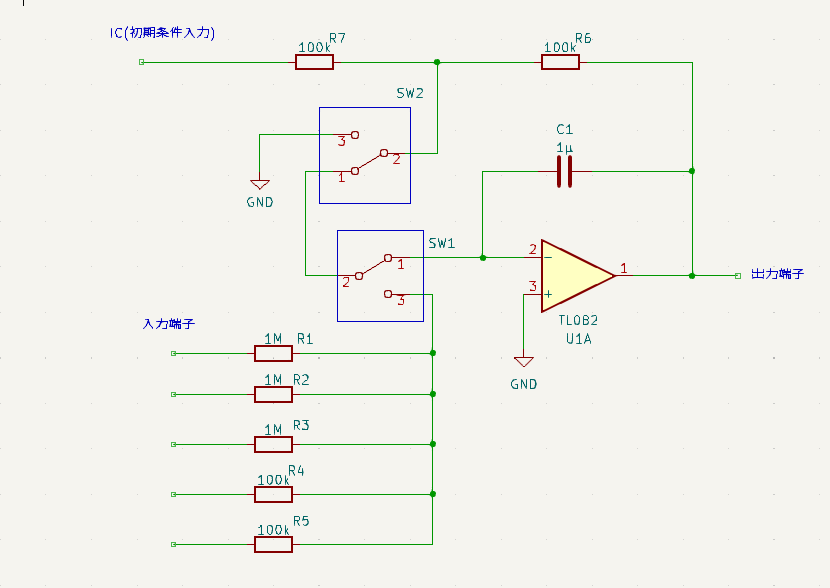
上の回路は低速型を想定し、C=1.0μFとしてある。(高速型の場合、C=1.0nFなどにするのが一般的である。)R1~R5は積分信号入力側の抵抗である。抵抗値を見れば、R1~R3に入力した信号はゲイン1倍、R4,R5に入力したものは10倍のゲインで積分出力されることが分かるだろう。R6,R7は初期条件を設定する抵抗である。 初期状態の時はR7を入力抵抗、R6をフィードバック抵抗とする反転器として動作し、演算状態になるとスイッチ(リレーやアナログスイッチ)で回路を切り替えて、R1~R5を入力抵抗、Cをフィードバックコンデンサとする積分回路として動作させる仕組みになっている。さらに、保持状態にするときは、演算増幅器とコンデンサから初期条件用抵抗と入力抵抗群の両方から切り離す必要がある。以上を踏まえると、図中におけるSW1,SW2の切り替え方は表のとおりになる。
| SW1 | SW2 | |
| 初期条件 | 端子1 | 端子1 |
| 演算 | 端子3 | 端子3 |
| 保持 | 端子3 | 端子3 |
表 積分器のモード切替に伴うスイッチ動作
- 初期条件 SW2及びSW1を通じて反転増幅器(ゲイン1)を構成し、初期条件入力端子に加わる電圧の符号反転値が出力に現れる。コンデンサは演算に関与しない。
- 演算 初期条件回路が切り離され、入力インピーダンスが入力抵抗群R1~R5に切り替わる。コンデンサによって積分が開始される。
- 保持 コンデンサと演算増幅器がいずれの入力インピーダンス素子とも切り離されるため、理想的な状態ではコンデンサの電荷がそのまま保持され、保持状態に移行した瞬間の出力電位を保つ。つまり積分が停止する。
この論理を実現するため、ふつうはデジタル回路が用いられる。
さて、重要なのは部品の選定である。積分器のコンデンサは当然無極性コンデンサである必要があるので、電解コンデンサなどではなく、比較的容量誤差を小さく作ることができるフィルムコンデンサが用いられる。積分器の誤差はアナログ計算機全体の演算誤差に大きな影響を与えるのでコンデンサの選定には多大な注意を払う必要がある。「アナログ電子計算機」(野村民也, 三浦武雄. コロナ社,1960) [1] の第8章「総合演算誤差」において、積分器を中心に各演算素子の誤差について数学的に議論しているので参考にしていただきたい。この本は1960年時点での技術を以てして達成できるアナログ計算機の演算誤差は、よくて0.1%であると主張するが、結局何十年たってもこの「0.1%」超えを安価に達成できるようなイノベーションは起きなかったので、結局この0.1%という数値がデジタル計算機とアナログ計算機の棲み分けの基準となったようだ。積分器の誤差要因は様々だが、積分コンデンサ由来のものでは、等価並列抵抗の存在に伴う「漏れ電流」と、コンデンサを短絡放電しても完全に電位が0にならずわずかに電荷が残ってしまう「誘電(体)吸収」という現象の2つが主要である。前者は低速型において、後者は高速型においてより顕著になり、相対誤差を増してしまう。漏れ電流が大きければ、例えば低速演算で解として正弦波が得られたとしても数十秒で振幅が減衰し、数分経てば半分以下になることもある。プログラムした式によっては逆に振幅が次第に発散する場合もあり、いずれも好ましくない現象である。それらの原因以外にも、入力抵抗同士の浮遊容量による誤差等もある。ゆえに高速型での繰り返し周波数(積分器の初期状態⇔演算状態を切り替える周波数)には上限がある。
以下は文献[1]のp288にある図表の引用である。あくまで60年代の情報であるので参考程度に留めてもらいたい。
.jpg)
.jpg)
.jpg)
当時はフィルムコンデンサとしてポリエチレンコンデンサやスチロールコンデンサ、マイラコンデンサが主流であったが、現在のポリプロピレンフィルムコンデンサの特性に敵うものではない。絶縁抵抗10GΩ~100GΩと、漏れ電流がとても小さく抑えられ、誘電体吸収も小さい高性能なコンデンサが開発されている。現代において、積分器のコンデンサとして選ぶならポリプロピレンフィルムが最適解であろうと思われる。ポリスチレンコンデンサは誤差を小さく作ることはできるが、容量のバリエーションが少なく熱にも弱いのでポリプロピレンフィルムコンデンサに幾分劣る。
抵抗値の誤差についても重要だが、これは積分器に限らず加算器・反転器などにも言えることである。金属皮膜抵抗で0.1%~1%のものを使えばある程度は使い物になるだろう。それ以上許容誤差を小さくしても、価格が指数関数的に増大してしまうだけで、コスト面から入力端子数に制限がかかる。コンデンサの公差が0.1%未満のものは同公差の抵抗のより製造が難しく、一般に大変高価であるため、他の演算要素の誤差が悪ければ抵抗値だけ良くても意味がないという点から考えるとあまりよろしくない。
巻線型の抵抗器を用いると高周波領域でインダクタンス成分に伴う誤差を生じるので、精度よく作ろうと思えば低速型の計算機にしか用いることができないだろう。
超精密級の大型商用アナログ計算機では、抵抗などのインピーダンスが恒温槽に入れられ、さらに基板上で金属板により抵抗同士が遮蔽され浮遊容量による結合を防いだというからすごいものである。
1.2 加算器・反転器
アナログ反転加算回路と反転増幅器そのものである。反転器は正負変換器ともいう。以下が加算器・反転器の出力電圧の関係式と記号である。
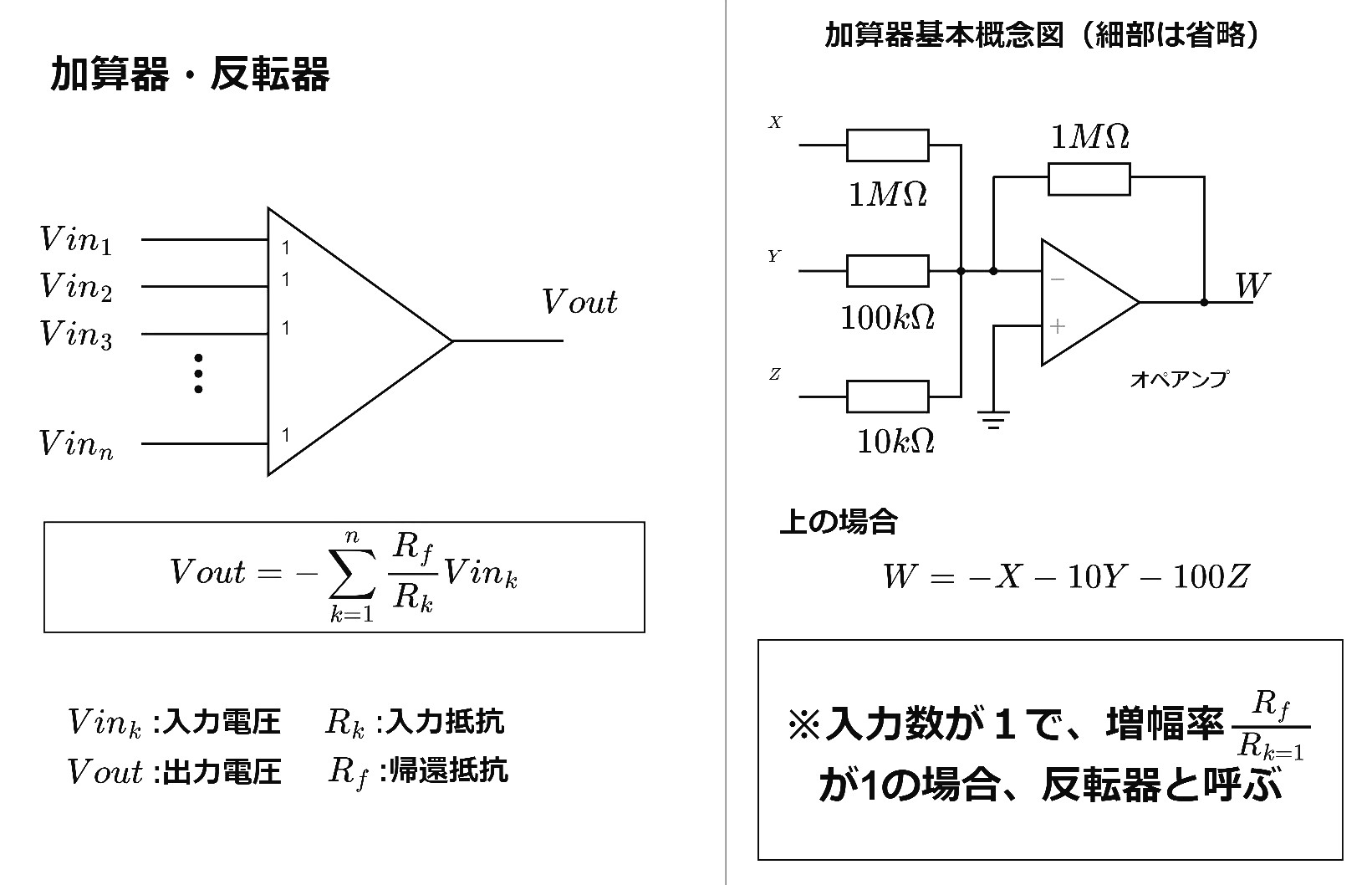
反転器は加算器の入力端子が1つの場合といえる。入力端子のゲインは積分器と同様、1倍,10倍が多い。(加えて2倍,4倍,5倍がある場合も。)
アナログ加算器は電圧の加算を行う演算器だが、実際には、電圧を入力抵抗で電流に変換し、キルヒホフの電流則による電流加算を行った後、オペアンプによるI-V変換回路でその電流和を再び電圧値に戻しているにすぎない。
また、高速繰り返しアナログコンピュータでは、フィードバック抵抗と並列に位相補償用の小容量コンデンサを接続する場合がある。
1.3 係数器
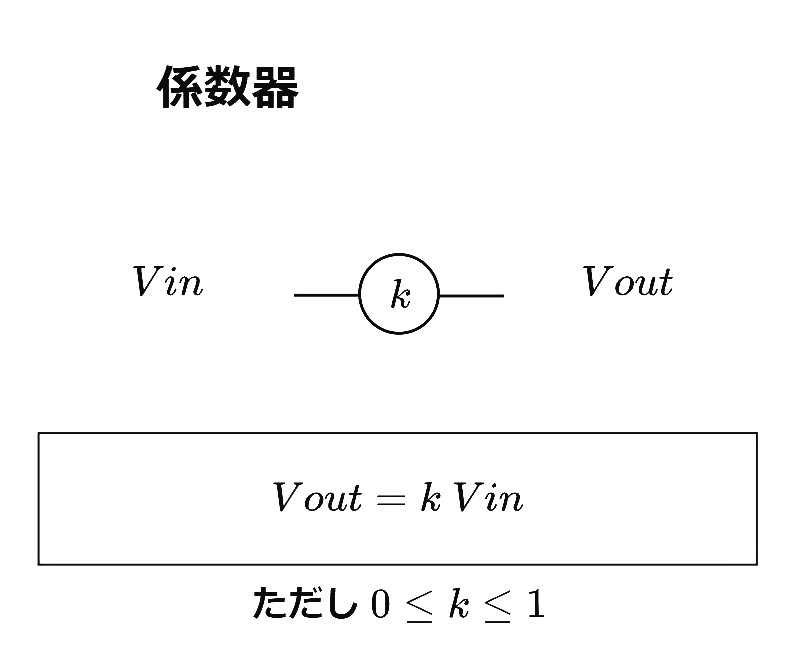
基本的に、可変抵抗器の一端を接地した「ポテンショメーター」である。精密設定ができる点から10回転ヘリカルポテンショメータが用いられる。この係数器で0~1の任意の係数\(k\)を設定できる。普通の商用アナログ計算機の加算器や積分器のフィードバックインピーダンスが1MΩや1μF(高速型の場合1nF等)固定で、入力抵抗が1MΩや100kΩ、200kΩ、400kΩ、500kΩなどとバリエーションを増やし、ゲインの種類を1倍、10倍、2倍、4倍、5倍もなどと設定できるようにしていたが、基本は1倍と10倍である。それらの端子の前に係数器を挿入すれば、合わせて\(k \times K\)のゲインが実現できる。ここで\(K\)は加算器や積分器のゲインである。係数器を0.24に、加算器のゲインが10倍の端子を選べば、合わせて2.4倍という中途半端なゲイン値を設定できるので、係数器は重要である。
しかしそのままでは出力インピーダンスが低く、係数器の出力を積分器や加算器等の入力に接続した場合に誤差が生じる。かつての商用アナログコンピュータは大抵ポテンショメーターそのままであったが、今はオペアンプが手軽に手に入る時代。ボルテージフォロワによるバッファー回路をすべての係数器の出力端子に入れることが可能である。。
1.4 乗算器
アナログコンピュータにおいて二つの従属変数の乗算を行うことは大変難しく、演算増幅器(オペアンプ)と受動素子の組み合わせで実現できない。係数を掛けるだけなら前記の係数器(係数ポテンショメーター)を用いればよいが従属変数の積はそう簡単にいかない。以下に様々な種類の乗算器を挙げる。
- サーボ乗算器 真空管式のアナログコンピュータの時代から広く使われている掛算の方法。サーボモーターとポテンショメータと差動増幅回路からなる。サーボ機構を利用するので低速型のみで用いられる。この文献に詳しい。
- 1/4二乗方式乗算器 \(xy=\frac{1}{4}(x+y)^2-(x-y)^2\)なる恒等式を利用すれば、2変数の乗算が加減算の線形演算と2乗演算の組み合わせで出来る。線形演算は加算器で行い、2乗演算はダイオードによる折れ線近似回路で放物線を近似して行う。
- その他:三角波乗算器・可変利得方式・変調方式・時分割式・半導体の2乗特性を用いる方式・ホール効果を用いる方式・特殊電子管を用いる方式など。
詳しくは「アナログ電子計算機」(野村民也, 三浦武雄. コロナ社,1960) 第五章「非線形演算器」p150~などを参照。
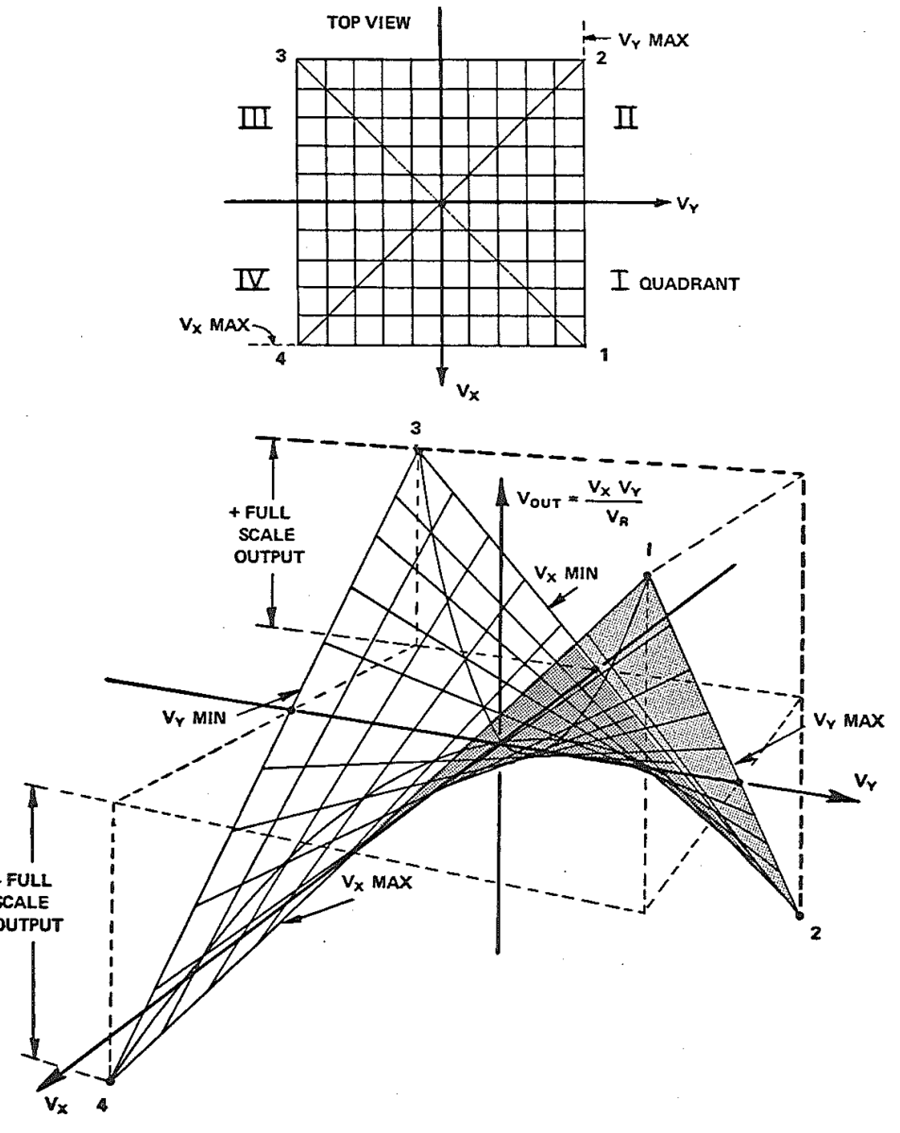
下図が乗算器の記号と入出力関係式。
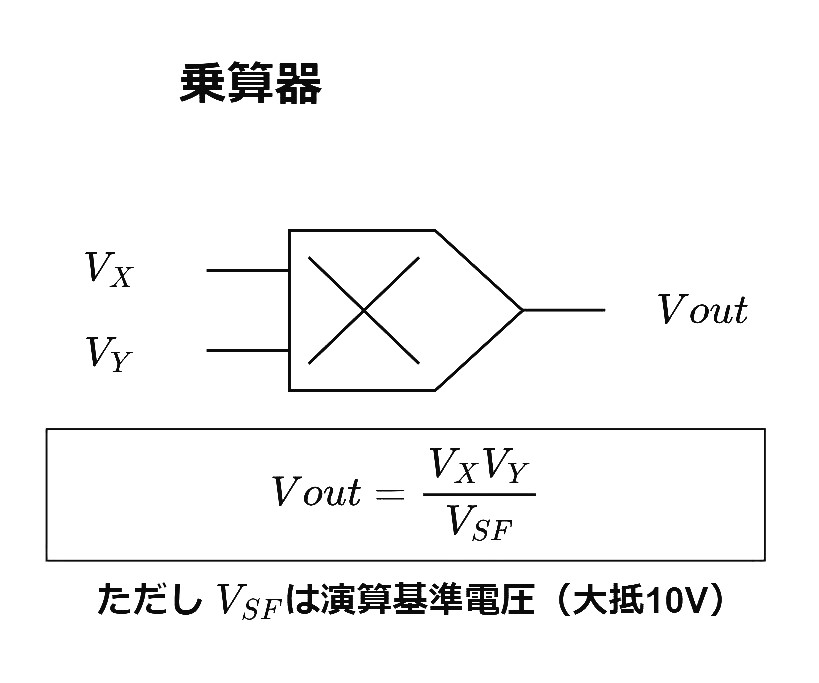
\(V_{SF}\)はスケール係数で、非線形演算に付き物である。10Vを「1」として計算するトランジスタ(or IC)式アナログコンピュータの場合この\(V_{SF}\)は10Vとなる。100Vを「1」とする真空管式であれば100Vとなる。この\(V_{SF}\)は、非線形演算の性質に関係する。一般に、同一単位の物理量の加減算では式の前後で次元は不変である(例えば1V+1V=2Vの加算のように)。この点から、線形演算は全ての演算器の入出力が等しく同次元(V)であるアナログコンピュータに適した演算と言えよう。しかし乗除算のような非線形演算だと話は変わってくる。1V×1V=2V\(^{2}\)というように、単位の次元が演算により変化してしまうのだ。それに伴い、演算器の入出力変数の単位は全て同次元であるという前提の元成り立っていた「10V→1」という対応付けが意味を失ってしまう。 例を挙げよう。10Vを「1」とする計算機の場合を考えると、「1×1=1」の演算を行いたいときは10V×10Vの電圧乗算を行うわけだ。しかし答えは100V(本当の単位はV\(^{2}\))として出力されてしまい、「1×1=10」という不正な演算が行われてしまうことになる。これを防ぐために、乗算器の出力は必ず電圧の次元を持つ係数\(V_{SF}\)で除される。そうすれば「1×1=1」の計算は(10V×10V)/10V=10V(→「1」)となり、次元の整合性がとれた正解が得られる。
乗算器は2変数の積を計算するから、非線形の微分方程式をアナログコンピュータで扱ううえで重要な要素である。しかし、数学で線形微分方程式として扱われるような式でも乗算器が必要になる場合がある。その1つが従属変数に独立変数\(t\)が陽に掛かっている式である。独立変数と従属変数の積の計算も「変数同士の積」にあたるから乗算器が必要になる。つまり、乗算器なしで解き得るのは厳密には定数係数線形常微分方程式に限られる。
その逆も言える。すなわち、非線形微分方程式を解くために必ず乗算器が必要になるとは限らない。主に工学上の諸問題を扱う際に出てくる「ガタ要素」「飽和要素」「不感帯要素」「階段関数」「履歴要素」などである。これらはある区間を定めてやればその範囲内では線形だが、全変域で考えれば非線形である。このような演算はダイオードを用いた折れ線近似回路などを利用すればよく、乗算器は必要ない。
乗算器の2入力端子を短絡し同一変数を与えるようにすれば二乗器ができるのは説明不要だろう。(同様にして、乗算器を2つ用いれば3乗演算も可能。)
1.5 除算器
また、乗算器と高利得増幅器(反転増幅器のフィードバック抵抗を除去した演算器)を用いれば、除算も行うことができる。下の図を見て頂きたい。
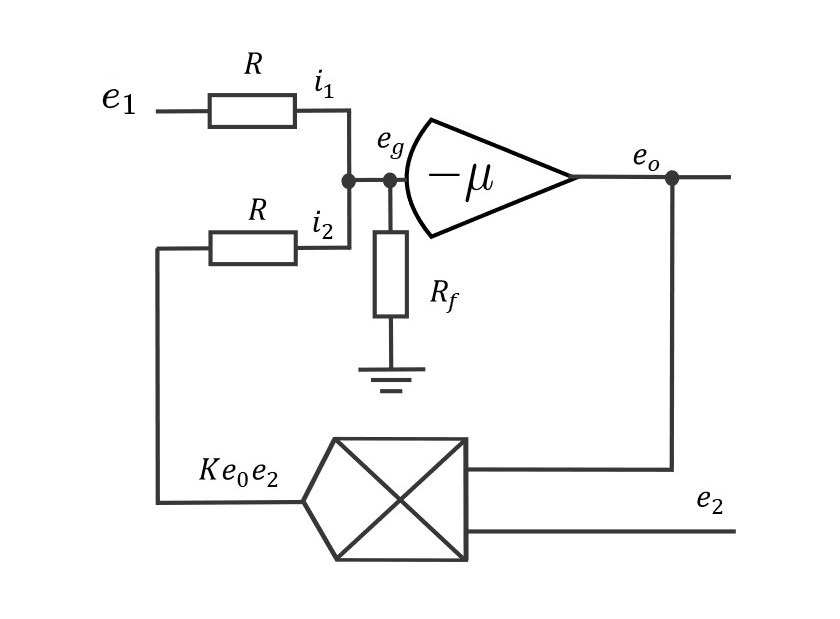
高利得増幅器は非反転入力端子(図では描かれていない)を接地したオペアンプだと思って頂いて差支えない。高利得増幅器に設けるフィードバック回路が抵抗のみであればそれは単なる「反転増幅回路」であるが、上の図ではその抵抗の前に乗算器が挿入されている。 \(\mu\)は増幅器のゲイン、\(K\)はアナログ乗算器の出力スケール係数( \(K=\frac{1}{V_{SF}}\)に注意 )、\(R_{f}\) は演算増幅器の入力インピーダンスとする。
オームの法則、および演算増幅器の働きから、以下の4式が直ちに得られる。
\begin{eqnarray}e_{g}&=&e_{f}(i_{1}+i_{2})\tag{1}\\\\i_{1}&=&\frac{e_{1}-e_{g}}{R}\tag{2}\\\\i_{2}&=&\frac{K e_{o}e_{2}-e_{g}}{R}\tag{3}\\\\e_{0}&=&-\mu e_{g}\tag{4}\end{eqnarray}
(1)に(2)および(3)を代入する。
\begin{eqnarray}e_{g}&=&R_{f}(\frac{e_{1}-e_{g}}{R}+\frac{K e_{o}e_{2}}{R})\\\\&=&R_{f}(\frac {e_{1}+K e_{o}e_{2}} {R} - \frac {2 e_{g}} {R} )\\\\\Leftrightarrow \quad e_{g}(1+\frac{2 R_{f}}{R}) &=& \frac{R_{f}}{R}(e_{1}+K e_{o}e_{2})\\\\\Leftrightarrow \quad e_{g}&=& \frac {e_{1}+ K e_{o}e_{2}} { \frac{R}{R_{f}} +2}\tag{5}\end{eqnarray}
\[e_{g}\approx \frac{e_{1}+K e_{o}e_{2}}{2}\tag{6}\]
関係式(4)を(6)へ代入して
\begin{eqnarray}-\frac{e_{o}}{\mu}&=& \frac{e_{1}+K e_{o}e_{2}}{2}\\\\e_{o}&=&\frac {-\mu e_{1} } {\mu K e_{2} + 2}\\\\&=&\frac {- e_{1}} { \frac{2} {\mu} +K e_{2} }\tag{7}\end{eqnarray}
\[e_{o}=-\frac { 1} {K }\frac { e_{1} } { e_{2} } \tag{8}\]
(8)式は、この回路で2変数電圧の除算がおこなえることを示している。また、係数は乗算器の出力スケール係数の逆数となっている。
上記回路においては、計算中は常に除算の分母の信号が正である必要がある。つまり、\(e_{2}\)は+0~+1 MU範囲に収まる変数のみ適用可能。もし\(e_2<0\)となれば、除算器ループが正帰還となり、演算回路は不安定になる。無論、分母が0になることも避けるべきである。
※ 除算器と同様の方式で平方根も生成可能である(乗算器を二乗器にすればよい)。これらを一般化すると、高利得増幅器のフィードバック部に\(f(x)\)で表される演算器を挿入したとき、その逆関数\(f(x)^{-1}\)生成や逆演算を容易に行える。これは陰関数法と称する演算回路構成法の一種であり、次章で詳しく述べることとする。
以上基本となる演算要素を概説した。他にも重要視される演算器は多数あるが、それらについてはたとえば文献「アナログ計算機の使い方」桑原道義 などを参照されたい。
2. 演算回路構成法
2.1 演算回路構成の手順
演算回路を構成する手順を概括すれば以下のようになる。
- 解くべき方程式(純粋な数学方程式でも、次元を持つ物理量を変数とする方程式でも構わない)を用意する。これを原方程式と呼ぶことにする。
- 原方程式の変数にスケーリング(電圧換算・時間換算など)を施し、演算方程式(計算機方程式)とする。原方程式が次元を持つ場合は、これで無次元の式となる。
- 演算方程式の形に合わせブロックダイヤグラムを組み、それに従いパッチボード(パネル)上で各演算要素の入出力端子同士を結線。
- 演算を開始し解を電圧波形としてオシロスコープやペンレコーダなどの出力装置で観測する。
以上は常微分方程式をアナログコンピュータで解く場合の手順である。微分方程式以外にも、アナログコンピュータで代数式( \(14+39\) や \(5^{}2\)などのような数式 )を解くこともできるが、これをアナログ計算機で解くことにあまりメリットがないので説明を省く。代数方程式を解くこともできるが、たとえば\(x^{2}+4x+3=0\)のような代数方程式はその変数を時間 \(t\)に変えて \(t^{2}+4t+3=0\)とすると、\(t\)の冪乗項は定数の縦続積分で生成できるため、アナログコンピュータではそれらを微分方程式とみなす。また、多元連立代数方程式や行列式も同様に常微分方程式に帰着でき、さらに偏微分方程式は差分近似によって連立常微分方程式に直すことができるため、いずれも常微分方程式の解法を応用できる。ゆえに以降の説明は微分方程式を解く場合について限定するので、その点ご了承いただきたい。
ちなみにアナログコンピュータが扱える変数は原理上実数の範囲に限られるが、オイラーの公式 \(e^{i\theta}=\cos{\theta}+i\sin{\theta}\)を応用して複素数変数を2変数実数関数と見做すことにより複素数の範囲にまでスコープを広げることもできる。(こちらは高次代数方程式の複素解求解に用いられるトリックである。詳細は「isograph(アイソグラフ)」という語で文献を検索してみて欲しい。)
基本的に上の手順に則って演算の方法を解説するが、本章では、すでにスケーリングが施された演算方程式が用意されている前提で解説する。スケーリングについては3章で詳しく説明するので、その旨念頭においていただきたい。
2.2 陽関数法と陰関数法
アナログコンピュータにおける演算回路構成法は大別すると以下のようになり、そのうち「陽関数法」と「陰関数法」が最も一般的な構成法である。

2.3 陽関数法
まずは陽関数法について解説する。陽関数法とは、最高微分階数項について陽に解ける常微分方程式に用いる演算回路の構成方法である。線形・非線形の如何や階数にかかわらず、この陽関数法で解ける場合がほとんどである。陽関数法の一般的な定義や概要を説明する前に、まずは簡単な例をお見せしたい。
以下の2階線形常微分方程式を解く場合を考える。\[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+\omega^{2}x=0\tag{9}\] ただし\(\omega\)は定数である。この式の解が正弦波\[A\sin{(\omega t+\phi)}\tag{10}\]となることはあまりにも有名である。(\(A\)と\(\phi\)は初期条件によって決まる定数)
この微分方程式は最高微分階数項について容易に解けるので、陽関数法が適用可能である。すなわち、\[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-\omega^{2}x\tag{11}\]
この式の形に合わせ、ブロックダイヤグラムを組む。
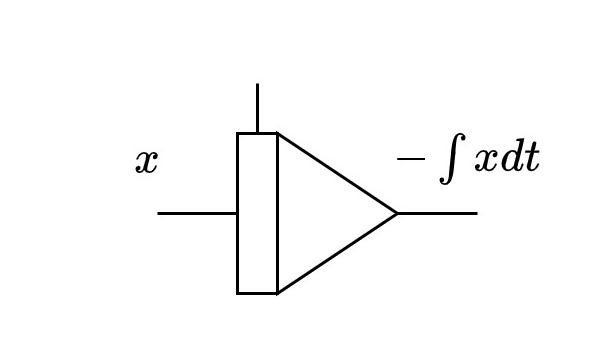
以前説明した積分器の記号である。以降入力端子のゲインは特記無き限り「1」であるとする。ここで注目すべきは、積分器の入出力の合いだに成り立つ関係である。アナログコンピュータにおける積分器は、「入力の時間積分の符号を反転したものを出力する」ので、入力を\(x\)とすれば出力は\(- \int x \mathrm{d}t\)と表される。しかし、見方を変えれば「入力は出力の時間微分の符号を反転させたものである」とも言えよう。これは微分と積分が互いに逆の演算であるという数学的事実に基づく。
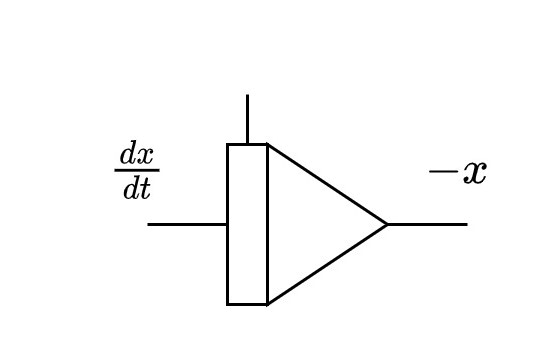
上の図はその関係を踏まえ入出力関係を書き直したものである。出力を\(-x\)とした場合、入力は\(\frac{\mathrm{d}x}{\mathrm{d}t}\)となる。
次に、積分器を2個縦続接続することを考える。
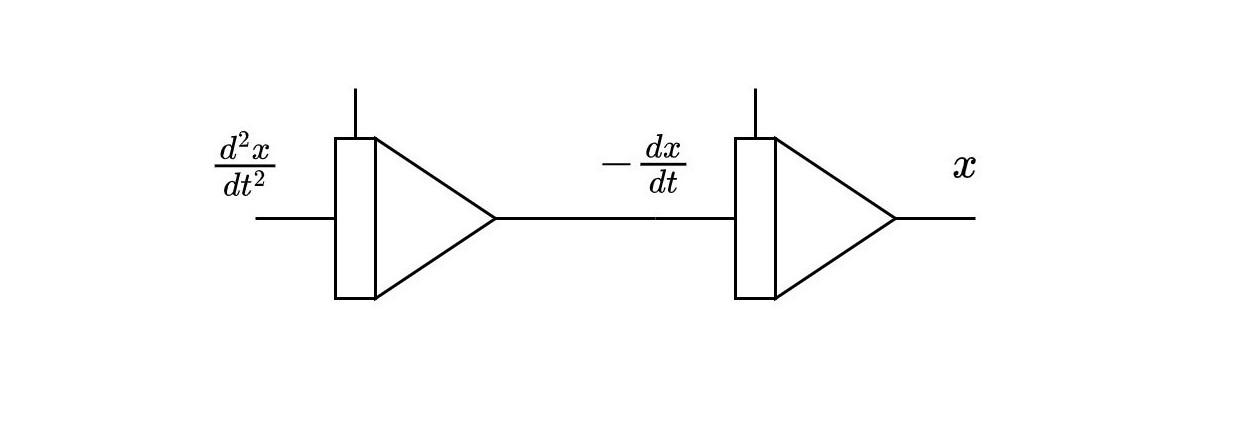
後段の積分器の出力を\(x\)とした場合、その入力は\(-\frac{\mathrm{d}x}{\mathrm{d}t}\)であり、それを出力とする前段の積分器の入力は、さらに時間微分された\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\)となる。回路中に積分器が挿入されるたびに符号が逆転することに注意して欲しい。
これで変数\(x\)とその2階時間微分が用意できたので、次に\[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-\omega^{2}x\tag{12}\] の等号部分を実現しなくてはならない。そのために必要なのが、以下のような「帰還(フィードバック)」である。
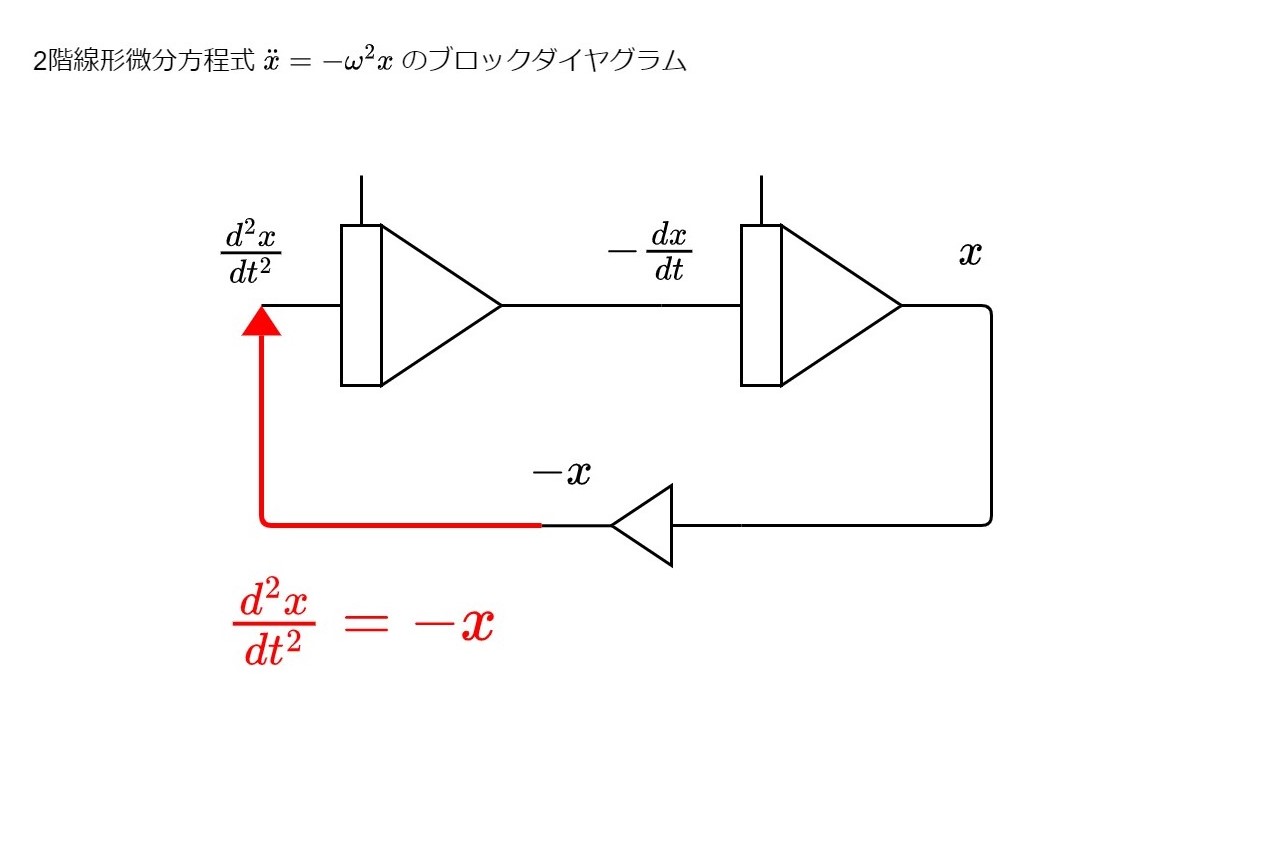
上の図は、\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-x\) なる関係式を演算回路中で実現するために、後段の積分器出力\(x\)を反転器で\(-x\)に変え、それを前段の積分器の入力に戻している。さらに、この帰還路を設けることにより初めて方程式中の等号を回路に落とし込めたことになる。さらに、\(-x\)に定係数 \(\omega^{2}\)を掛けるため係数器を以下のように挿入する。
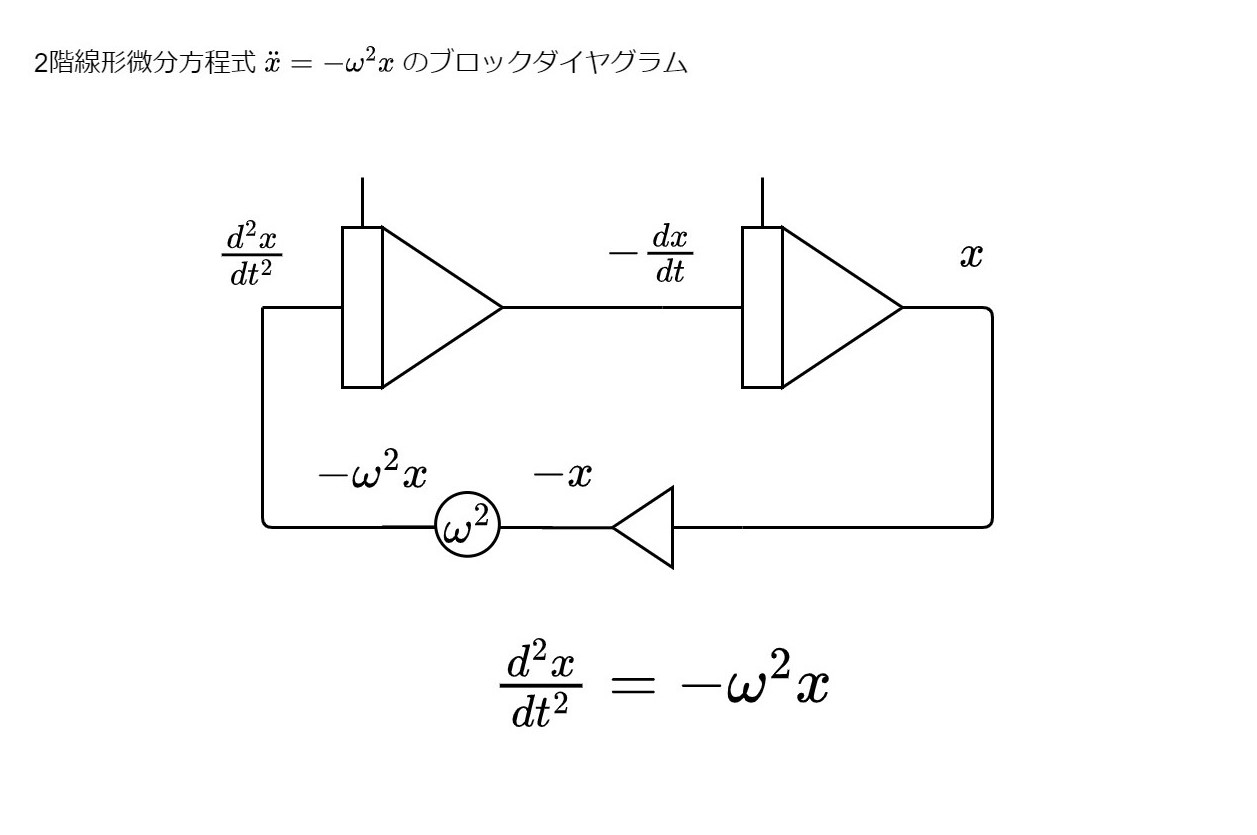
これで\(\frac{\mathrm{d}^{2}x}{dt^{2}}=-\omega^{2}x\)という方程式を表現する演算回路を構成できた。
しかし、この回路をそのまま動かしても解を出力することはない。忘れてはならないのは、常微分方程式がその階数だけ任意定数を含むということである。つまり、\(n\)階常微分方程式ならば\(n\)個の積分器それぞれに初期条件を設定しなくてはならないのだ。線形斉次方程式の解のうちすべての初期条件が0であるものは\(x(t)=0\)ただ1つのみであるから、このままでは解の正弦波は永久に出力に現れず、0Vのままである。
積分器の出力電圧は、初期条件入力端子に加えた電圧を \(V_{ic}\)とすると、\[V_{out}=-\int V_{in} \mathrm{d}t-V_{ic}\tag{13}\] つまり積分器の初期条件入力端子に加えた電圧の符号が逆転した値が初期条件として与えられる。
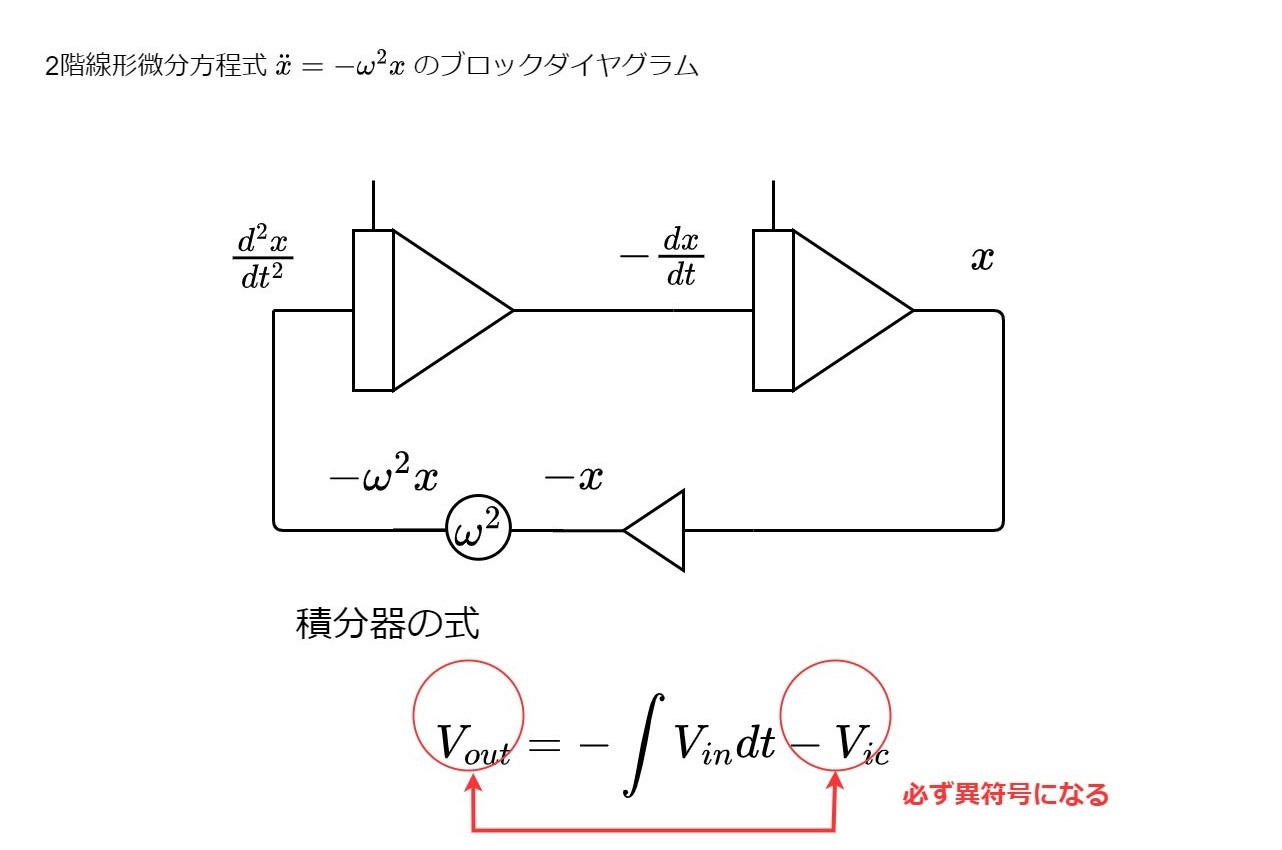
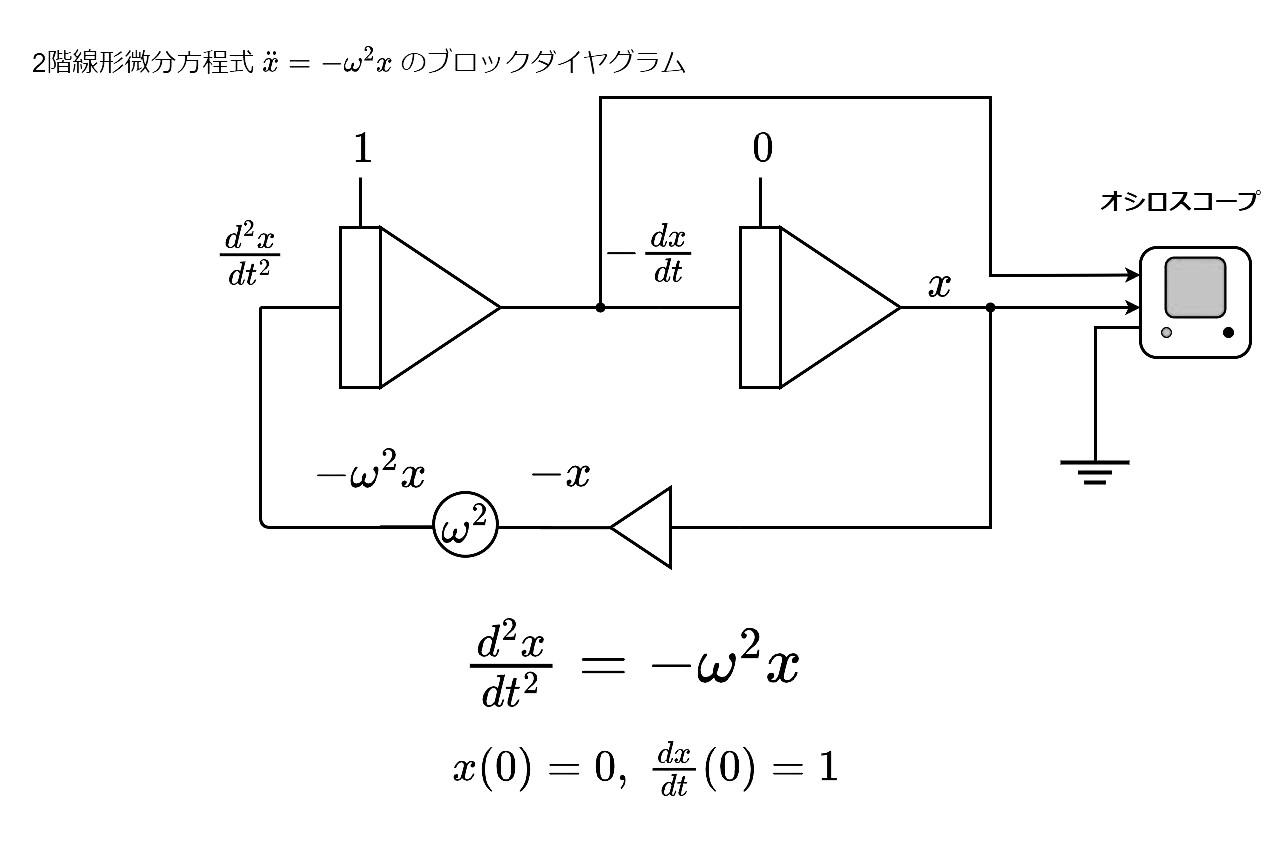
\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-\omega^{2}x\)の場合は \(x(0)\)と\( \frac{\mathrm{d}x}{\mathrm{d}t}(0)\)の2つの初期条件を設定しなくてはならない。仮に\(x(0)=0\),\( \frac{\mathrm{d}x}{\mathrm{d}t}(0)=1\)としたら、下図のように設定することとなる。
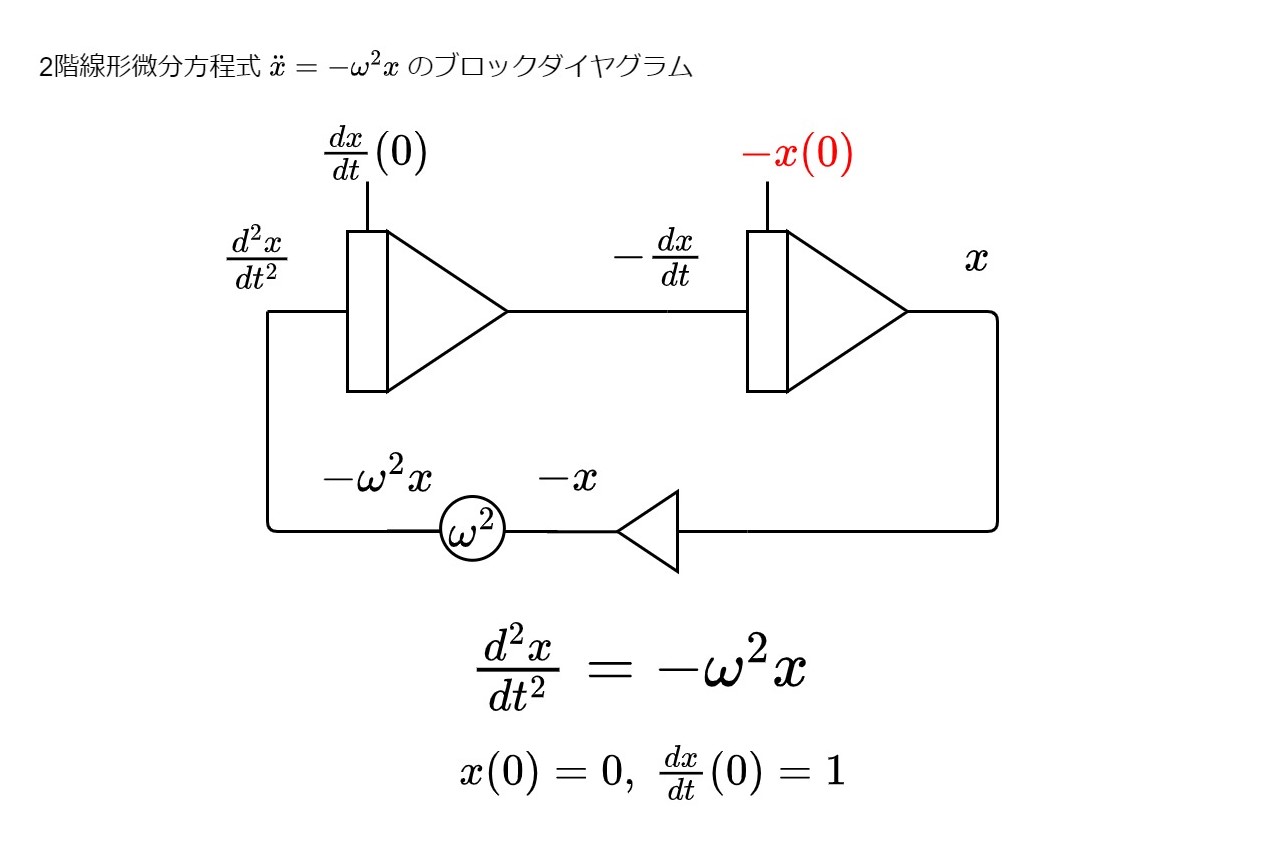
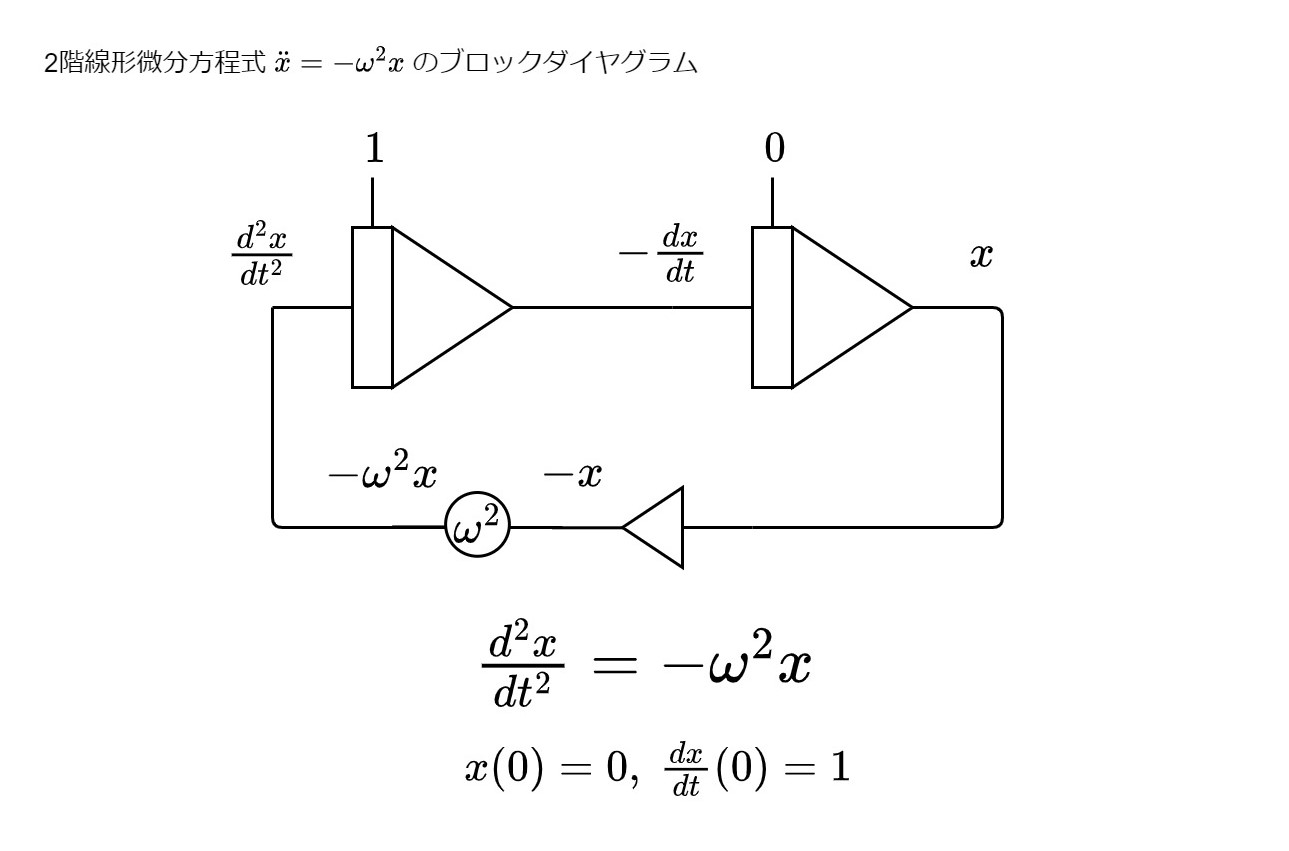
以上で演算回路の構成は完了した。以下のようにオシロスコープなどに接続して各変数の波形を見ることができる。
これまでの説明を踏まえ、さらに\(n\)階の常微分方程式に拡張したうえで陽関数法の概念を示したものが以下の図である。
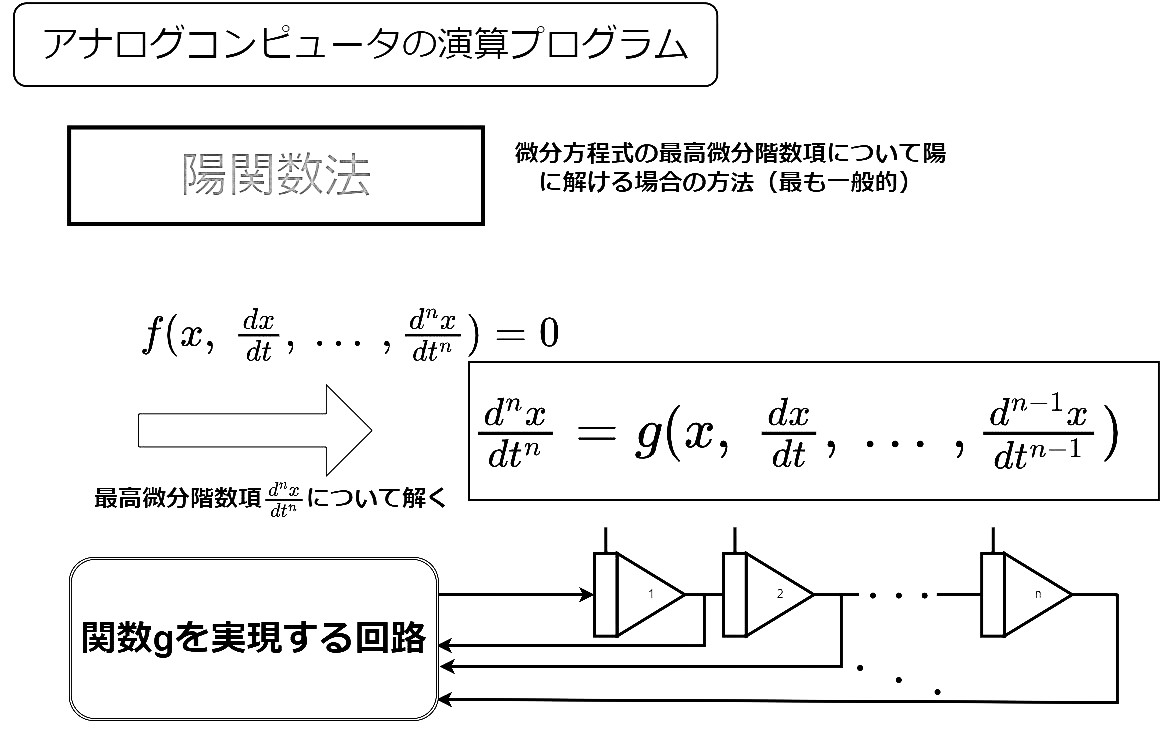
\(n\)階の常微分方程式 \[f\Bigl( \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \Bigr)=0\tag{14}\] を最高微分階数項について解くと \[\frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}=g\Bigl( \frac{\mathrm{d}^{n-1}x}{\mathrm{d}t^{n-1}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \Bigr)\tag{15}\] となるとする。図の下の回路を見ればわかるが、この関数\( g\)は変数\( x\)とその微分値を入力とし、最高微分階数項を出力として最前段の積分器に接続する回路部分に相当する。陽関数法で構成された演算回路は、大きく分けてこの関数\( g\)を実現する回路と積分器の\(n\)段縦続回路の2つからなるのだ。ちなみに前述の\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-\omega^{2}x\)の例だと、この関数\(g \)を実現する回路に相当するものは反転器に他ならない。単純な式の形をしているので、入力は\( x\)の1つのみである。
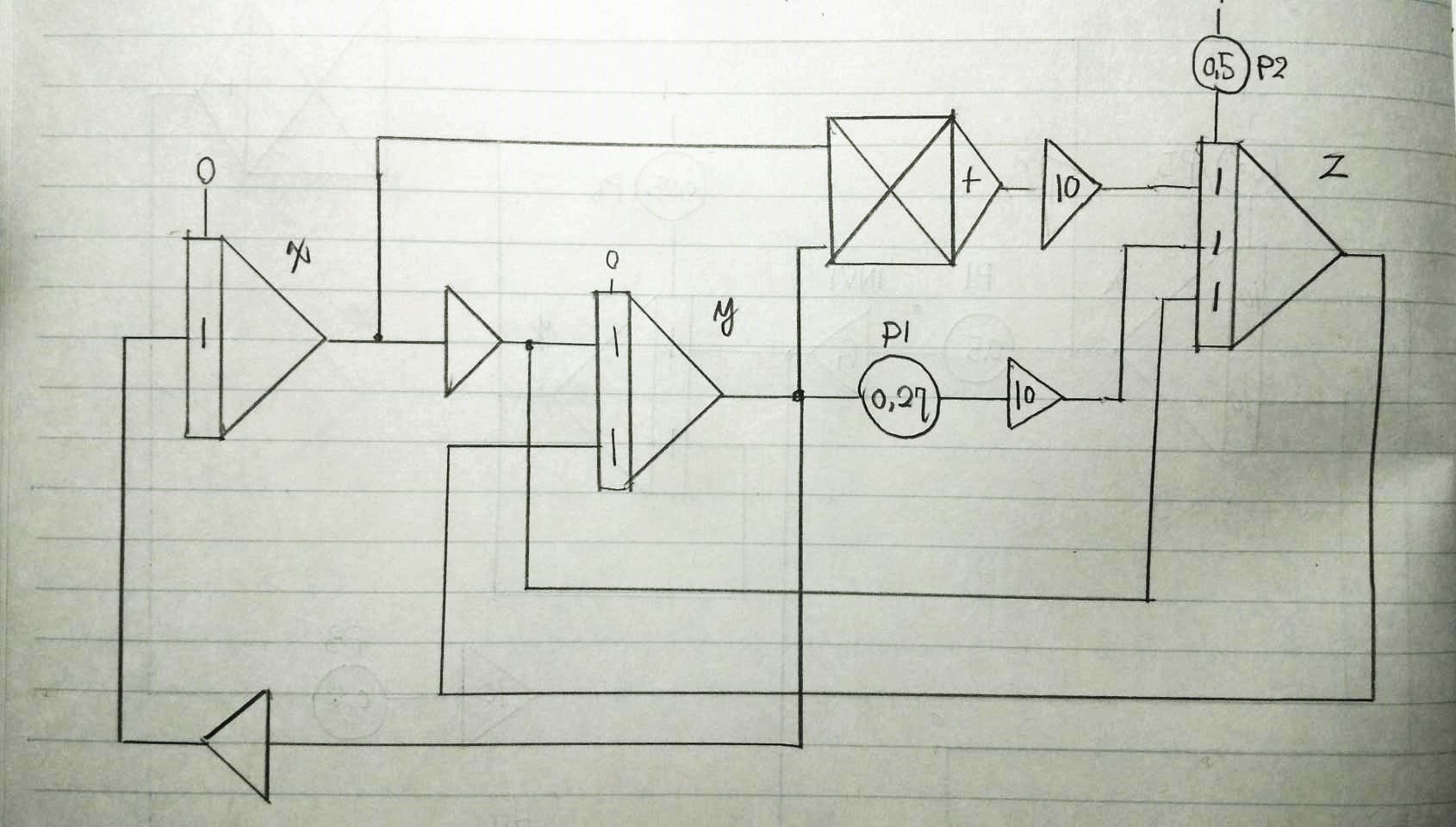
上図はもう少し複雑な例。私の自作したアナログコンピュータ試作機で、とある3元連立1階微分方程式を陽関数法で解いた時のブロックダイヤグラムのメモである。1階だが変数が3つ( \(x,y,z\) )あるので積分器も3つ必要である。注意して線を追うと、それぞれの積分器の入力には自身やほかの積分器の出力がフィードバックされていることが分かるだろう。また、非線形の方程式であったのでフィーバック途中に乗算器が挿入されている。
陽関数法は常に安定して計算が行えるということにメリットがある。ここで言う「安定して計算が行える」とは、「演算回路内の微小擾乱が発生した時、その擾乱が発散的に増大して解が不安定になり誤差が大きくなることがない」という意味である。これを数式で示そう。微小時間に発生した積分器の入力側の擾乱(ノイズ)を\(\phi(t)\)とすると、出力側に出てくる影響分は、\[\lim_{\Delta t\rightarrow 0} \int_{t}^{t+\Delta t}\phi(t)\mathrm{d}t=\lim_{\Delta t \rightarrow 0}\phi(t) \Delta t=0\tag{16}\] と0に収束する。陽関数法ではすべての帰還ループに必ず積分器が存在するわけだが、それらの積分器が擾乱を抑えるため、自他の積分器入力に伝わることは無い。よって、 \[\frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}=g\Bigl( \frac{\mathrm{d}^{n-1}x}{\mathrm{d}t^{n-1}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \Bigr)\tag{17}\] の関数\(g\)の入力変数 \( \frac{\mathrm{d}^{n-1}x}{\mathrm{d}t^{n-1}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \) 各々に現れる微小変位が他の変数に伝搬することがなく、解の安定性を懸念する必要がないことが分かる(文献[1] p260)。
ただし、擾乱の発生する以前の時間のうち演算回路の各信号値が正常な(発散・飽和してない)時間が存在する(帰納的に、時間原点近傍では少なくとも無限大など異常値ではない)場合に限るという前提条件が隠れている。 たとえ陽関数法で構成された演算回路であっても、正帰還が大きい微分方程式の場合、擾乱の増幅云々の議論以前に解自体が発散してしまうだろう。 たとえば\[\frac{\mathrm{d}x}{\mathrm{d}t}=x\tag{18}\]の解は、\(A\)を任意定数とし、\[x=Ae^{t}\tag{19}\]と指数関数的に増大する。無限大に発散する前の解関数の挙動を観察しやすくするため、 時間換算係数(後述)を小さくして時間軸を引き延ばす工夫が必要である。もちろん無限大に発散する出力波形もその微分方程式の解であることに変わりはないし、 その意味ではアナログコンピュータは正常に作動しているということになる。良くも悪くもアナログ計算機は人間が結線した通りに動きその結果を吐き出すだけであるから、人間の工夫・配慮が肝要である。 そういうところはデジタル計算機におけるプログラミングと似ているかもしれない。
2.4 陰関数法
続いて陰関数法を説明する。乗算器の項で説明した除算器の構成法も陰関数法の1つの例である。
陽関数法との対比から明らかだが、陰関数法は最高微分階数項について陽に解かず、陰表的な式をそのまま演算回路に落とし込む方法である。つまり、\(n\)階常微分方程式 \[f\Bigl( \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \Bigr)=0\tag{20}\] が与えられたとき \[\frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}=g\Bigl( \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}},\frac{\mathrm{d}^{n-1}x}{\mathrm{d}t^{n-1}} , ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \Bigr)\tag{21}\] のように\(\frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}\)が右辺に残ったまま実装する。当然ながら、この世の全ての微分方程式が最高微分階数項について陽に解ける(式変形できる)とは限らない。一方、全ての常微分方程式は最高微分階数項について陰表的な表式に変形することができるので、陰関数法は陽関数法を一般化した解法であり、どの常微分方程式にも適用できるといことが言える。陰関数法が適切な例としてV.Bushが挙げたのが \[ \epsilon^{\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}}+\sin{\Bigl(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}-t\Bigr)+\frac{\mathrm{d}x}{\mathrm{d}t}-tx=0}\tag{22}\] である。これは超越方程式の一種であるが、\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\)について陽に解くことができないのは明らかである。このような式は陽関数法ではなく陰関数法で実装するほかない。
しかし、最高微分階数項について陽に解ける常微分方程式であっても、陰関数法を用いた方が適切である場合がある。ヒルの微分方程式の一種である以下の式 \[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+\frac{k^{2}x}{1+a\cos{\omega t}}=0 \tag{23}\] がその一つ。この式は\( \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\)について容易に解けるが、割算器が必要になる。割算器が使えないとき、\(\frac{1}{1+a\cos{\omega t}}\)なる時間関数を積分器と乗算器で発生させて別の乗算器で\(k^{2}x\)と掛け合わせなければならず、回路が複雑になってしまう。そうするよりも、\[\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-(a\cos{\omega t}) \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} -k^{2}x\tag{24}\]のように陰表的に表して実装することで、非線形演算器が乗算器1つのみの簡単な回路で済ませたほうがよい。
他の例としてラゲールの微分方程式を紹介する。\[ t\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+(1-t)\frac{\mathrm{d}x}{\mathrm{d}t}+nx=0 \tag{25}\]これは最高微分階数項について陽に解き得るのだが、陰関数法による実装が望ましい部類に入る。これを陽に解くと、\[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}=-\frac{(1-t)\mathrm{d}x/\mathrm{d}t+nx}{t}\tag{26}\] のように独立変数\(t\)が分母に来てしまう。これをそのまま割算器で実装すれば、\(t=0\)の近傍で割算器の出力が飽和してしまい、演算回路は上手く動作しない。また、ベッセルの微分方程式 \[ t^{2}\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+t\frac{\mathrm{d}x}{\mathrm{d}t}+(t^{2}+n)x=0\tag{27}\]も同様である。
陰関数法は、陽関数法のように必ずしも安定な回路になるとはかぎらない。ゆえに、陰関数法における安定性の如何は非常に重要になってくるのだが、それについては次節でまとめて解説する。
2.5 陰関数法の安定条件
陽関数法ではすべてのループ(帰還路)が積分器を通るため、擾乱(ノイズ)に対してきわめて安定である。しかし、陰関数法では不用意な回路構成だと動作が不安定になる場合がある。アナログコンピュータで陰関数法を用いるとき、その回路が安定する条件を知っておくことが肝要である。
2.5.1 一般の方程式の場合
\[f(x, x_{1}, ... ,x_{n})=0\tag{28}\]という式の解\(x\)を陰関数法で求める問題を考えよう。\(x_{1}~x_{n}\) は\(x\)についての従属変数若しくは独立変数である。(この場合関数 \(f\)は代数方程式であり、このような演算回路を求根器と総称する。)まずは上式の\(x\)を陰表的に括り出す。つまり両辺に\(ax\)の項を加えたのち、定数\(a\)で割る。 \[ ax+f(x, x_{1}, ... , x_{n}) =ax\tag{29}\] \[ \therefore x=\frac{1}{a}f(x, x_{1}, ... , x_{n})+x \tag{30}\] さらに右辺を新たな関数としておき、\[ x=g(x, x_{1}, ... , x_{n}) \tag{31}\]とする。この操作は一般の方程式で必ず可能である。解きたい方程式を陰表的式に直す際、この定数 \(a\)をどのように選べば陰関数法の回路が安定するか知ることがいま我々が目指すことである。
関数\(g\) を実現する回路の出力\( x\)を\( x_{1}, ... , x_{n}\)を実現する\(n\)個の回路に導き、その\( n\)個の各出力を関数\(g\) を実現する回路の入力へ帰還させる一連のループが必要になるが、それとは別に、出力\(x\)自体を\(g\)の入力に直接帰還するループが1つ現れる。演算回路を簡単に図示すると以下のようになる。
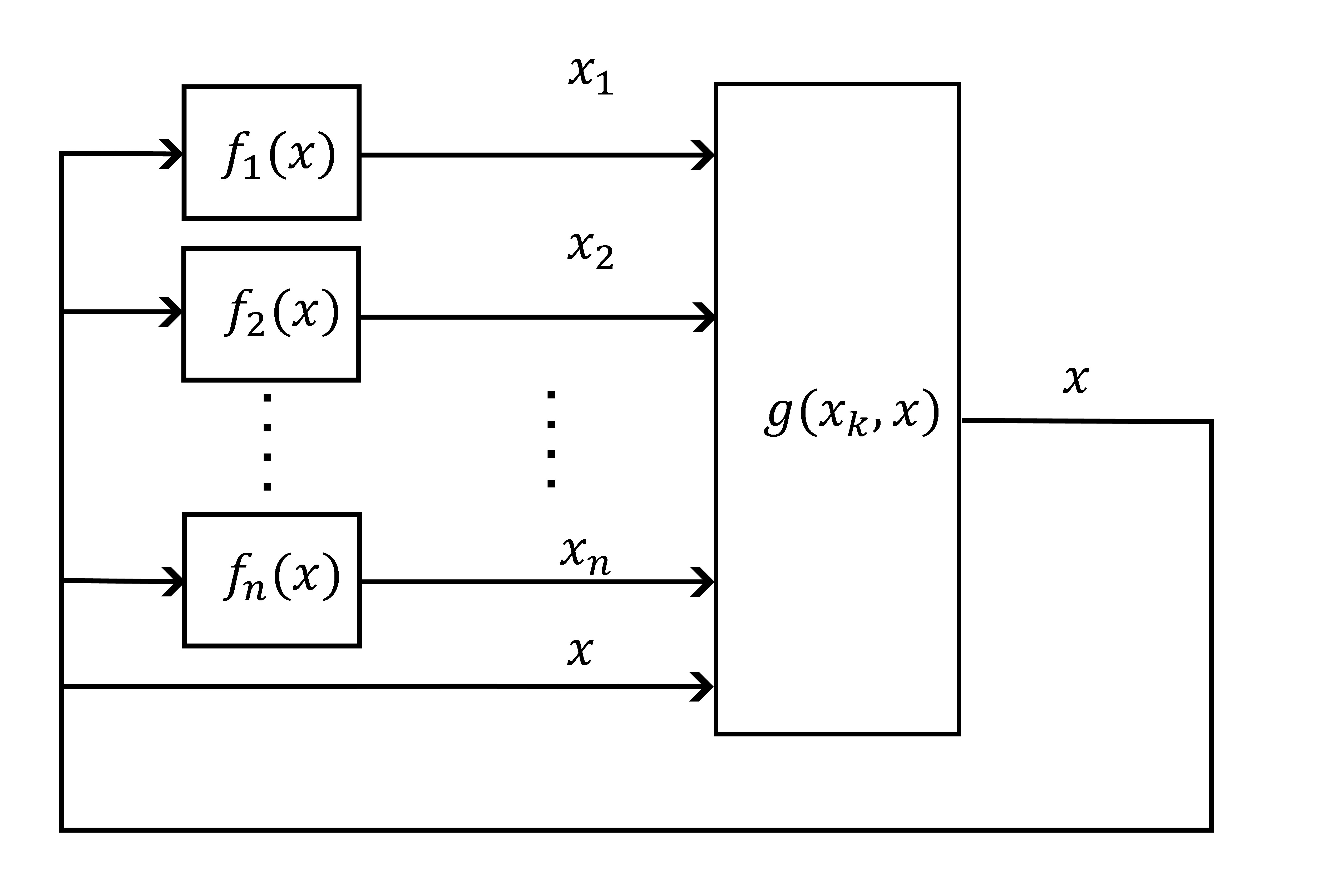
いま、\[ x=g(x, x_{1}, ... , x_{n})\tag{32}\] \[ x_{k}=f_{k}(x) \tag{33}\] と置き、\(g\) の出力端子を切り離し仮想的に信号 \( y\) を加えるとする。このとき \[ x=g(x, x_{1}, ... , x_{n})\tag{34} \] \[ x_{k}(=f_{k}(x))=f_{k}(y)\tag{35}\] となる。\(x, x_{1}, ... , x_{n}\)が\(y\)の関数であることに注意し、(27)式を \(y\) について微分すると、\[ \frac{\mathrm{d}x}{\mathrm{d}y}=\frac{\mathrm{d}g}{\mathrm{d}y}+\sum_{j=1}^{n} \frac{\partial g}{\partial x_{k}}\cdot \frac{\mathrm{d}x_{k}}{\mathrm{d}y}\tag{36}\]という式が得られる。この\(\mathrm{d}x/\mathrm{d}y\)という微係数は、\(y\)の増分に対する \(g\) の出力 \(x\) の変化率である。回路が安定になる条件は、\(g\)の出力\(x\)に発生した擾乱(ノイズ)が増幅されないことなので、この変化率が1より小さくなればよい。つまり、\[\frac{\mathrm{d}g}{\mathrm{d}y}+\sum_{k=1}^{n} \frac{\partial g}{\partial x_{k}}\cdot \frac{\mathrm{d}x_{k}}{\mathrm{d}y}<1\tag{37}\]である。 \(\frac{1}{a}f(x, x_{1}, ... , x_{n})+x =g(x, x_{1}, ... , x_{n})\)とおいたのだから、安定条件は\[\frac{1}{a}\Bigl(\frac{\mathrm{d}g}{\mathrm{\mathrm{d}y}}+\sum_{k=1}^{n} \frac{\partial g}{\partial x_{k}}\cdot \frac{\mathrm{d}x_{k}}{\mathrm{d}y} \Bigr)<0\tag{38}\]と書ける。ただし、この情報だけでは安定な\(a\)の値は一意には定まらないことを申し添えておく。
2.5.2 微分方程式の場合
前項は \(x_{1}, ... , x_{n}\)が\(x\)の一般の従属変数である仮定の下行った議論である。今度は少し特殊化して、それらが\(x\)の時間積分値であるとき、すなわち\(f()\)が微分方程式である場合の安定性を考察しよう(アナログコンピュータで解きたい数式は微分方程式であることがほとんどであるため、この限定は有意義である)。
改めて \[f\Bigl( \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x \Bigr)=0\tag{39}\] と表せる常微分方程式を考える。前述したように、両辺に\(a {\mathrm{d}^{n}x}/{\mathrm{d}t^{n}}\)を加えて\(a\)で除し、左辺の関数を新たに\(g\)とおくことで\[\frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}=g( \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}, \frac{\mathrm{d}^{n-1}x}{\mathrm{d}t^{n-1}}, ... , \frac{\mathrm{d}x}{\mathrm{d}t}, x )\tag{40}\]のような陰表的式に直す。演算回路は以下のようになる。
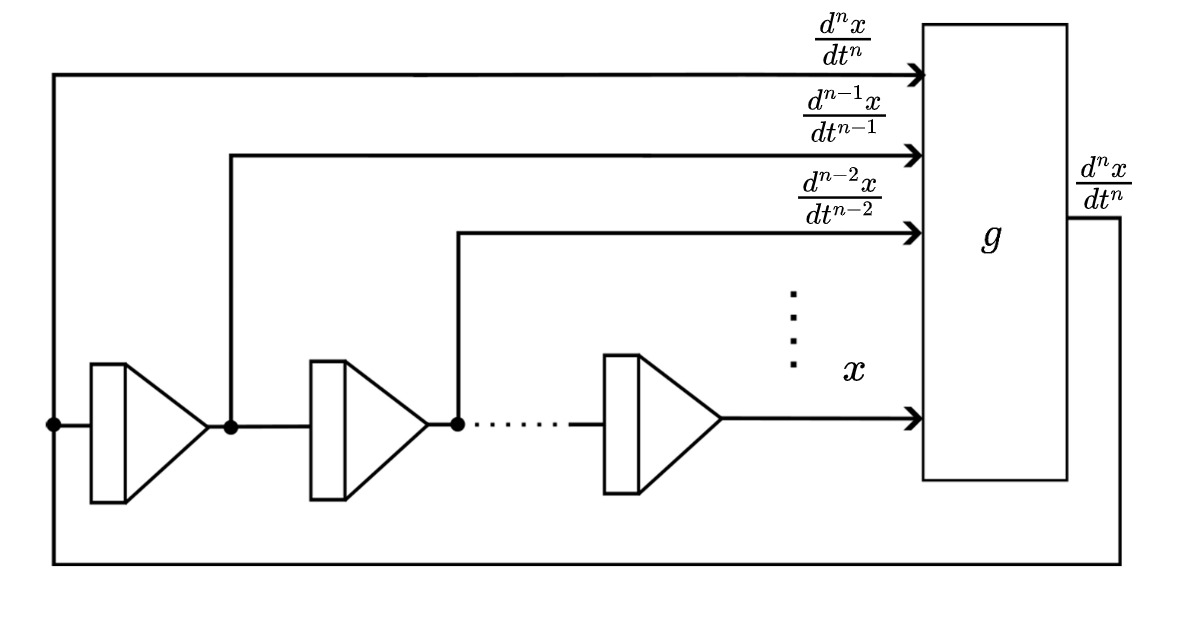
上の図中の積分器記号は純粋な「積分器」である必要はなく、すくなくとも積分器を1つ含み、他の時間演算要素(微分器など)を含まない回路を指していると思っていただいて差支えない(例:一次遅れ要素)。 関数 \(g\) の回路に帰還する信号には、少なくとも1つの積分器を挟んで帰還する信号\( x , ... , x^{(n-1)}\) が\(n\)個と、\(g\)の出力が積分器を介さずにそのまま戻される帰還信号1個があることが分かる。前者は、陽関数法の項で説明したとおり以下の式で安定性が保証されている。\[\lim_{\Delta t\rightarrow 0} \int_{t}^{t+\Delta t}\phi(t)\mathrm{d}t=\lim_{\Delta t \rightarrow 0}\phi(t) \Delta t=0\tag{41}\] ローパスフィルタの働きをする積分器の存在のおかげで、この帰還路についてはノイズ\(\phi(t)\)が増幅されることがない。しかし、直接帰還される最高微分階数項 \(x^{(n)}\)は必ずしも安定するとは限らないので、回路全体の安定の如何はこの帰還路の安定性にかかっている。すなわち、\[\frac{\partial g}{\partial \frac{\mathrm{d}x^{n}}{\mathrm{d}t^{n}}}<1\tag{42}\] が陰関数法における回路全体の安定条件となる。\(g\)ではなく\(f\)で表すと、\(n\)階常微分方程式の陰関数法回路における安定条件は
\[\frac{1}{a} \frac{\partial f}{\partial \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}}<0\tag{43}\]
となる。求根器の場合導かれた安定条件の式から\(a\)を一意に定めることはできなかったが、\(f\)が微分方程式であるという強い仮定のもと導かれた上式であれば\(a\)の値が一意に定まる。我々にとっては嬉しい結果である。
※注※
実はこの不等式は回路が安定するための十分条件であり、必要十分条件ではない。\(\frac{1}{a} \frac{\partial f}{\partial \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}}=0\)の場合でも、すべての変域にわたって、より高位の偏微分係数値が \[ \frac{\partial^{2} f}{\partial \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}^{2}} = ... = \frac{\partial^{(k)} f}{\partial \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}^{(k)}}=0 , \qquad \frac{\partial^{(k+1)} f}{\partial \frac{\mathrm{d}^{n}x}{\mathrm{d}t^{n}}^{(k+1)}}<0 \tag{44}\]を満たせば回路は安定になる(ただし\(k\) は自然数とする)。また、前提条件として関数\(f\)内に微分器を含んでいないことも必要である。演算回路の安定性についてのより厳密な議論は、文献[1] p.250~p.271 または 文献[2] (藤田広一. 「アナログ計算機のプログラム」昭晃堂,1978.) p.84 にくわしい。
具体例を通して理解していただくため、簡単な例題を用いて安定な陰関数法回路を構成する方法を説明する。
例題1
以下の方程式を陰関数法により実装したい。どのような陰表的式に変形すればよいか、適切な式の例を1つ挙げよ。
\[\dot{x}+x=0\tag{45}\]
解法
上式は陽関数法で解くのが普通だが、本題では陰関数法で解くよう指示があるのでそれに従う。\[f(\dot{x}, x)=\dot{x}+x\]と定めよう。例のごとく両辺に\(a \dot{x}\)を加えて\(a\)で除せば、\[\dot{x}=\frac{1}{a} f(\dot{x}, x) +\dot{x}\tag{46}\]一方、\[\frac{\partial f}{\partial \frac{\mathrm{d}x}{\mathrm{d}t}}=1\tag{47}\] 陰関数法の安定条件を適用すれば、\[\frac{1}{a} \frac{\partial f}{\partial \frac{\mathrm{d}x}{\mathrm{d}t}} = 1/a<0\tag{48}\] よって\(a<0\)を満たせば良いことが分かる。ゆえに、(46)式を演算回路に直す際、負の値を定数\(a\)として選べばよい。例えば\(a=-2\)とすると、\[\dot{x}=- \frac{1}{2} f(\dot{x}, x)+\dot{x}\] \[\therefore \dot{x}=\frac{1}{2}(\dot{x}-x)\tag{49}\]となる。
※\(a=-1\)でも安定だが、それでは右辺の\(\dot{x}\)が消えて陽表式になってしまい、題意を満たさない。
(解法おわり)
以上は陽関数法でも解き得るごく簡単な式であったが、今度はもう少し複雑な例を挙げよう。前に引例したヒルの微分方程式 \[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+\frac{k^{2}x}{1+a\cos{\omega t}}=0 \tag{50}\] の場合、\[-a\cos{\omega t}<1\tag{51}\]が陰関数法の安定条件となるが、\(|a|<1\)の場合は安定に解け、\(|a|\geq1\)では陰関数法は不適であることが分かる。式の安定性の判断を1定数の評価のみをもとにして行えるので大変便利である。
2.6 最急降下法
最急降下法はデジタル電子計算機での最適化アルゴリズムの一つとして有名だが、アナログ電子計算機でも適用可能である。
例として2元連立方程式
\[\left\{\begin{array}{ll}f_1\bigl(x_1\,,x_2\bigr)=0\\f_2\bigl(x_1\,,x_2\bigr)=0\end{array}\right.\tag{52}\]
を考えよう。代数方程式だろうが微分方程式であろうが構わない。つまり、\(x_1,x_2\)が独立変数についての関数でも、また\(f_1\)や\(f_2\)が微分項を含んでいてもいい。
まず、(52)式の右辺の0をそれぞれ\(\delta_1\,,\delta_2\)と置く。
\[\left\{\begin{array}{ll}f_1\bigl(x_1\,,x_2\bigr)=\delta_1\\f_2\bigl(x_1\,,x_2\bigr)=\delta_2\end{array}\right.\tag{53}\]
\(\delta_1\,,\delta_2\)は元の式の形からの誤差を表していると考えられる。(52)の連立方程式を解くことは、\(\delta_1\,,\delta_2\)が同時に0になるように\((x_1\,,x_2)\)を定めることと同じである。すなわち、
\[D(x_1\,,x_2)=\delta_1^2+\delta_2^2\tag{54}\]
を0に近づける(最小にする)ことを考えればいい。Dは\(x_1-x_2\)座標上のスカラー場であるので、その勾配が定義できる。
\[\operatorname{grad}D=\left(\frac{\partial{D}}{\partial{x_1}}\,,\frac{\partial{D}}{\partial{x_2}}\right)\tag{55}\]
解\(\boldsymbol{x}=(x_1\,,x_1)\)を初期位置から極小点へ向かわせるため、その速度ベクトル
\[\boldsymbol{v}=\mathrm{d}\boldsymbol{x}/\mathrm{d}t=\left(\frac{\mathrm{d}x_1}{\mathrm{d}t}\,,\frac{\mathrm{d}x_2}{\mathrm{d}t}\right)\tag{56}\]
を再急降下方向、すなわち\(-\operatorname{grad}D\)と一致させる。
\[\left\{\begin{array}{ll}\frac{\mathrm{d}x_1}{\mathrm{d}t}=-\frac{\partial{D}}{\partial{x_1}}=-2f_1\frac{\partial{f_1}}{\partial{x_1}}-2f_2\frac{\partial{f_2}}{\partial{x_2}}\\\\\frac{\mathrm{d}x_1}{\mathrm{d}t}=-\frac{\partial{D}}{\partial{x_2}}=-2f_1\frac{\partial{f_1}}{\partial{x_2}}-2f_2\frac{\partial{f_2}}{\partial{x_2}}\end{array}\right.\tag{57}\]
上記の連立式の演算回路を陽関数法で構成し、積分器の初期条件入力端子に初期値を加えると、定常状態において回路の出力は解へ収束する。陰関数法では必ずしも安定な演算回路ができるとは限らなかったが、最急降下法は必ず安定して解けることが大きな利点である。
この方法は、連立代数方程式をアナログ計算機で解きやすい1階の連立常微分方程式として解くことができるほか、ゼロ除算の生じる割算やそれを含む微分方程式を安定に解く回路にも応用できる。後者の場合、適切な初期値を与え、解信号の周波数に応じた適切な積分器のゲインを選ぶことにより、定常値に収束するまでの過渡現象および定常誤差はかなり軽減されるはずである。
2.7 電流加算点をダミー変数とする方法
単に「高利得増幅器を用いる方法」として言及される場合もある。主に式中の除算などで特異点が生じている(最高階が変数係数である)微分方程式を安定して解くために用いられる方法である。このメソッドについて特に普及した名称が無いようなので、勝手ではあるが上記のように命名した。初出は米国特許 Kurokawa et al. "Setup system in analog computer," US pat. US3652843A, 1972.である。黒川一夫氏らを考案者と考えてよいだろう。また、書籍[2]の第3章では、「スケーリングに便利な方法」として簡単に言及されているので、そちらも参考にして欲しい。
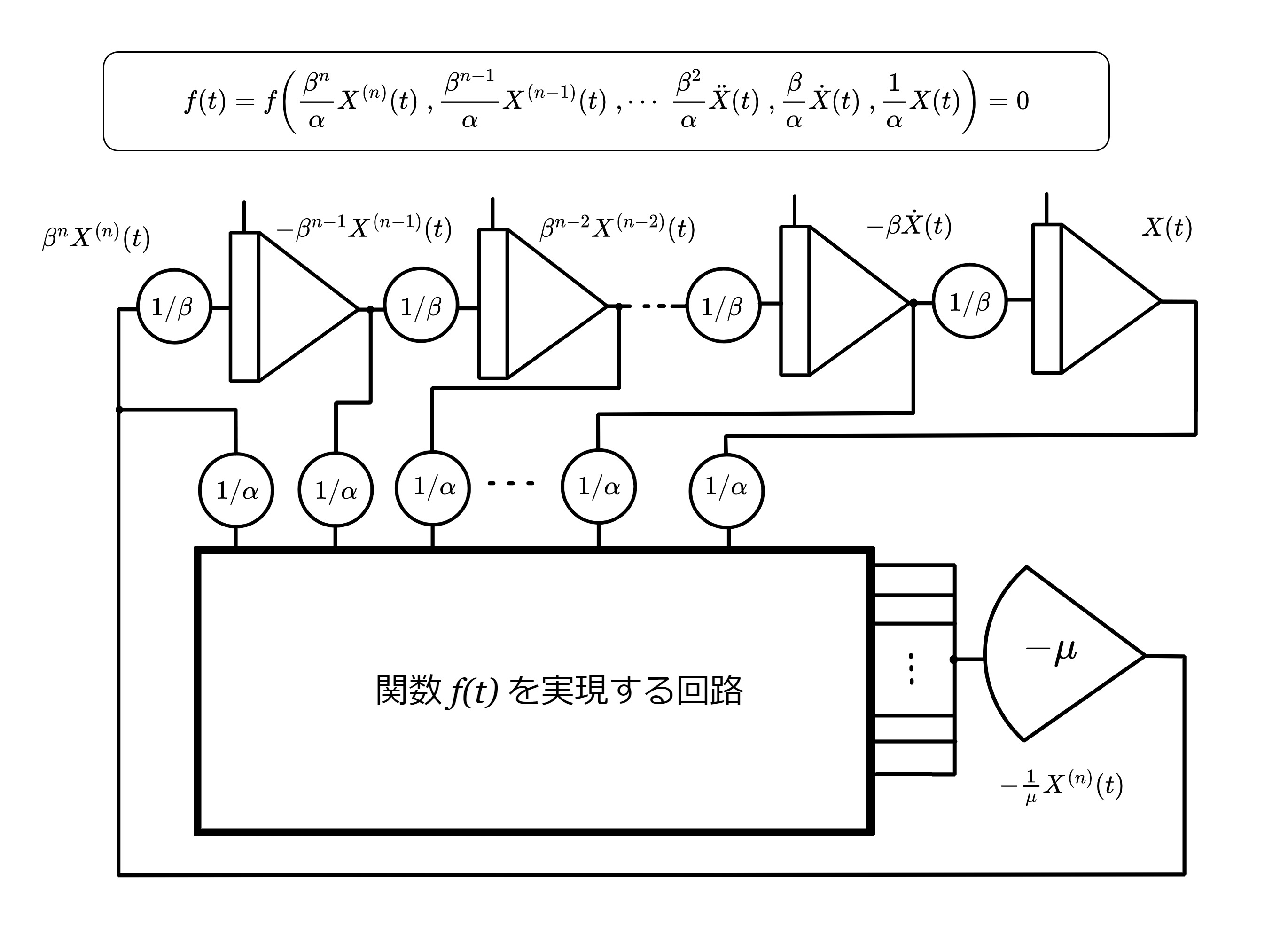
この方法は厳密には陰関数法の一種であり、微分方程式の右辺の0を高利得反転増幅器の入力部電流加算点(バーチャルショートで常に電位が0)の電位として回路を構成する方法である。たとえば、n階常微分方程式
\[f(t)=f\bigl(x^{n}(t)\;,x^{n-1}(t)\;,\cdots\;\ddot{x}(t)\;,\dot{x}(t)\;,x(t)\bigr)=0\tag{58}\]
の演算方程式は、電圧換算係数を\(\alpha\)、時間換算係数を\(\beta\)とすると
\[f(t)=f\biggl(\frac{\beta^n}{\alpha}X^{(n)}(t)\;,\frac{\beta^{n-1}}{\alpha}X^{(n-1)}(t)\;,\cdots\;\frac{\beta^2}{\alpha}\ddot{X}(t)\;,\frac{\beta}{\alpha}\dot{X}(t)\;,\frac{1}{\alpha}X(t)\biggr)=0\tag{59}\]
となる(換算係数については第4章で説明する)。
ここで、上式の右辺をダミーの変数
\[0=-\frac{X^{(n)}(t)}{\mu}\tag{60}\]
に置換する。\(\mu\)は高利得増幅器のオープンゲインであり、通常無限大とみなせる。(ゲインの大きい積分器としてもよい。)入力インピーダンスを無限大とすれば、いかなる入力信号に対してもダミー変数は0を維持する。演算回路は次のようになる。
図からわかるように、時間換算係数と電圧換算係数を独立して設定できるのが本方法の強みである。
前述の例では最高階項\(X^{(n)}(t)\)をダミー変数として選んだが、\(X^{(n+1)}(t)\)などでも構わない。微分方程式の最高階項以上の項を設けて演算回路を構成することで、最高階の係数に独立変数\(t\)が存在するため陽関数法では実装が困難な微分方程式を除算なし・特異点なしの演算方程式にできる。
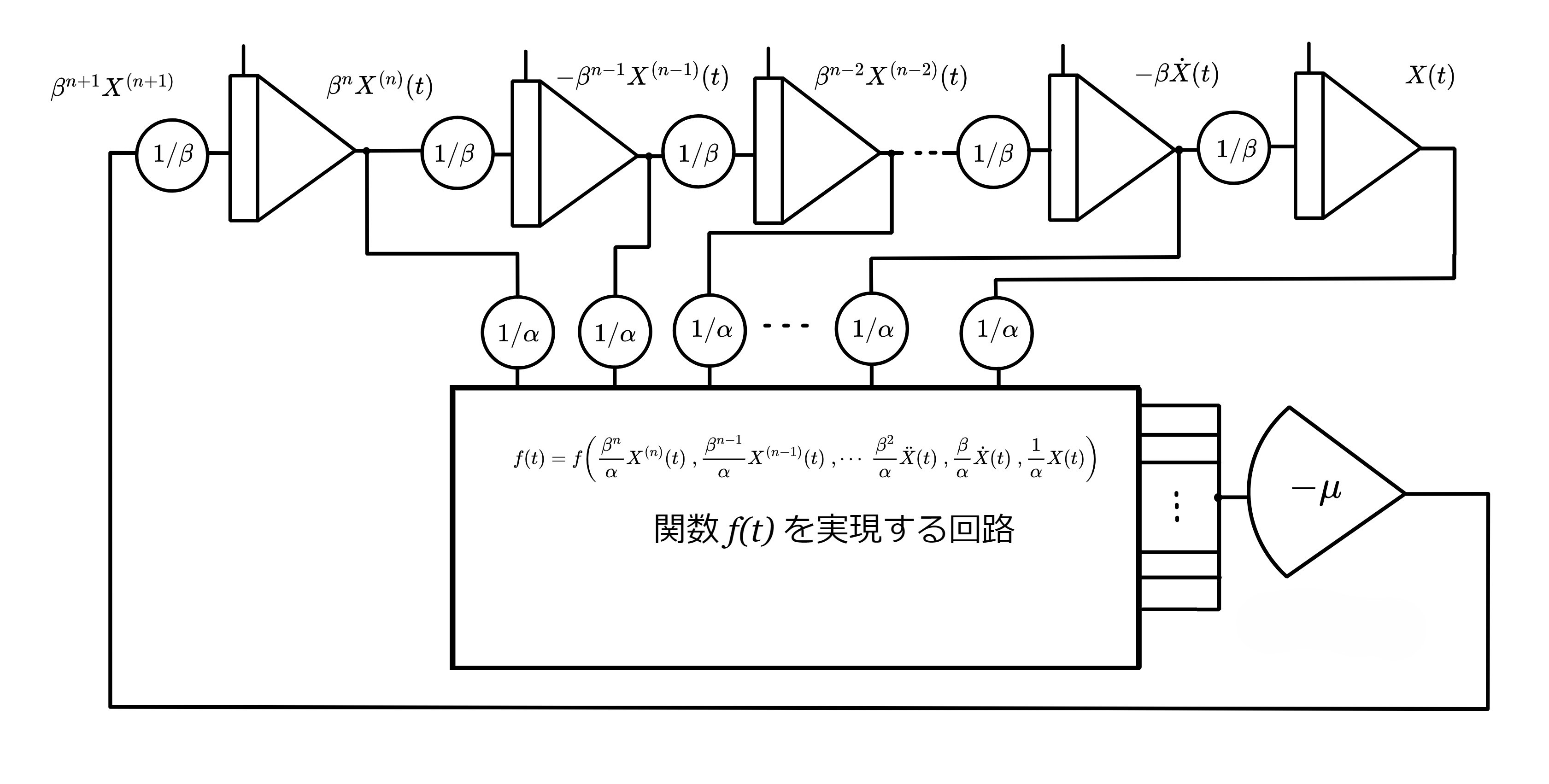
最高階項の符号は、上の例ではマイナスをつけたが、原方程式を実現する上で、理論上では正符号であっても問題ないはずであるが、式の形によって不安定な演算回路になる可能性もある。正と負のどちらを選ぶかは、演算回路中のマイナーループの安定性(正帰還か負帰還か)を総合的に見て決定すると良い。
なお、オープンループの高利得増幅器のかわりに、高ゲイン(小帰還容量)積分器を使っても同様の効果が得られる。
ベッセルの微分方程式・ラゲル(ラゲール)の微分方程式・ルジャンドルの微分方程式などの、ラプラス方程式やヘルムホルツ方程式を球座標や円筒座標で変数分離した後に現れる式は、得てしてself-adjointな微分方程式になることが多く、そのような常微分方程式は各微分項について展開すると最高階に独立変数が掛かる。それらの式は、陽関数法ではなく上述のようなトリックを用いてアナログ演算回路を構成する方法が有用である。
3. スケーリングと演算方程式
アナログコンピュータは電圧値を方程式の変数値に見立てて演算を行うが、演算回路の主要要素をなす演算増幅器(オぺアンプ)にはダイナミックレンジが存在し、扱える値に限界がある。オペアンプは電源電圧(±15Vなど)より大きい電圧信号は飽和して潰れてしまい、あまりにも微小な信号はノイズに埋もれて相対誤差が増してしまう。時間軸についても同様で、信号周波数が高すぎると誤差が増してしまう。低速型の場合、ペンレコーダに対して適切な周波数はせいぜい10Hz程度であり、それ以上の高周波信号には追随できず、不正確な解を記録してしまう。信号周波数が低すぎるのも時間の不経済であるからなるべく避けたい。演算の正確性と、レコーダやオシログラム上での可読性を高めるためには、電圧軸・時間軸ともに適切な範囲内に収める必要がある。その作業がスケーリングである。本章では、解きたい元の数式(原方程式)の変数をスケーリングして、アナログコンピュータで実装可能な式(演算方程式)に変換する方法を解説する。
3.1 スケーリングとマシンユニットの概説
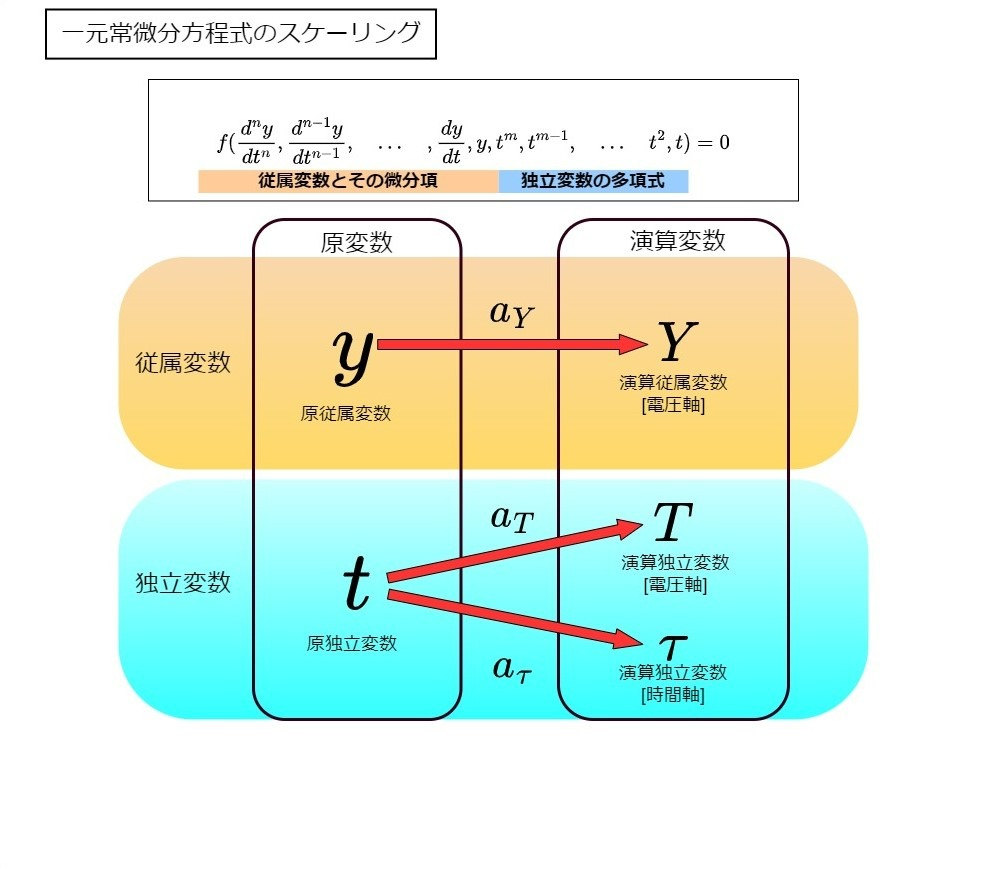
アナログコンピュータで解きたい方程式を原方程式(original equation)という。原方程式中の変数を原変数(original variable)と称する。原変数は、無次元変数であったり、あるいは長さの次元などを持つ物理変数であることも考えられるだろう。以後基本的に1元常微分方程式(従属変数・独立変数ともに1種類のみ含まれる微分方程式)の場合を考えるが、便宜上、その原従属変数(original dependent variable)の単位を[d.u.]、原独立変数(original Independent variable)の単位を[i.u.]と定める。
無論、原方程式をそのままアナログコンピュータにプログラムすることはできない。電子式アナログコンピュータでは従属変数を電圧信号として、独立変数は時間として扱うわけだから、次元を[d.u.]から[V]へ、[i.u.]から[s]へ変換する必要がある。その際、原変数と電圧信号を1対1で対応させる(原変数の1N、1m、1℃... などを1Vとする)ことは一般に上手くいかない。ある原変数の最大値が\(10^3\)m/sだったとして、1対1対応させると1000Vという高電圧を扱う必要が出てくる。当然ながらアナログコンピュータではそのような高電圧を扱うことはできない。ゆえに、ある一定の変換係数を掛けて縮小させる(逆に小さすぎる場合は拡大させる)必要がある。独立変数についても同じことがいえる。
このように、原変数に対し適切な変換を行うことをスケール変換/スケーリング(scaling)という。また、スケール変換に際し原変数に掛ける係数を変換係数/スケールファクター(scaling factor)という。アナログコンピュータで微分方程式等を解きたいとき、ブロックダイヤグラムを組む前にこのスケーリング操作を行う必要がある。
しかしながら、原変数と電圧値の間を変換する変換係数を定めて直接結びつけるのでは以下に述べるような不都合が生じてしまう。
電子式アナログコンピュータで演算するには、どの電圧値を原変数の1とするかを決めなくてはならない。しかし、一般的に計算機によって扱える電圧値というのは異なる。トランジスタ式のアナログ計算機なら十数ボルト、真空管式のアナログ計算機ならば数百ボルト程度までの電圧信号を扱える。真空管式の計算機の使用を想定し、100Vを原変数の「1」と定めて、原変数-電圧値間の変換係数を定めたとしよう。しかし、より小さい電圧レンジ(たとえば±10V)を持つ計算機を用いて同じ原方程式を解く場合、その変換係数はもはや意味をなさなくなるため、あらたに変換係数を設定する必要が出てくる。すなわち、原変数と電圧値の間を直接変換係数で結びつけてしまうと、計算機のレンジに応じて新たな変換係数を設定する作業が生じる恐れがあるのだ。大変不便である。
この不都合を解決するため、原変数と電圧値を換算係数で直接結び付けるのをやめてみよう。計算機によって、何ボルトを原変数の1にするべきかが異なるわけだから、変換係数はその基電圧値に依存しないほうがいいだろう。具体的には、電圧値を「正規化」すればよい。つまり、原変数の1に相当する電圧値をあらかじめ決めておいてマシンユニット/計算機単位(machine unit)とする。そして、計算機上で扱う変数値は、電圧値ではなくマシンユニットに対する「比率量」で考る。それを演算変数/計算機変数(machine variable)と名付け、変数の最大値(正確には変数の絶対値の最大値)がマシンユニットを超えないように換算する。たとえば10Vを原従属変数の1としたい場合、マシンユニットは10Vであり、計算機上における6.5Vという電圧値は演算変数では0.65となる。アナログコンピュータの演算器同士の結線を表すブロックダイヤグラムでは、変数や定数値などは原変数でも電圧値でもなく全て演算変数で表す。マシンユニット・演算変数の導入には次のような利点がある。
- 演算変数に基づいたブロックダイヤグラムと換算係数は、いかなる電圧範囲のアナログコンピュータでも適用できる
- 変数を全て無次元量として扱える
原変数が小文字の記号で表される場合、その演算変数は原変数と区別して大文字で表す(例:原変数が\(y\)のとき、演算変数は\(Y\))。ただし、独立変数\(t\)については特別である。従属変数と独立変数の違いを強調して、独立変数の演算変数をあらわす文字としてギリシャ文字の\(\tau\)を用いる。アナログコンピュータでは従属変数は電圧値(の比率)として扱うが、独立変数は純粋な時間として扱うという大きな違いがあるため、両者は根本的に異なるものであり、混同してはならない。
なお、演算従属変数の書き方については、書籍によっては単に原変数を[y]のように[ ]で囲んで表す流儀もあるので注意。(たとえば文献 [3] など。) 私は文献 [1] に従い演算変数を大文字にする方式を採った。今後特記無き限り原従属変数の大文字表記を演算変数、\(\tau\)を演算時間(独立変数の演算変数)とする。
ちなみに、かつての商用アナログコンピュータでは、トランジスタを用いたアナログコンピュータの場合はマシンユニットとして10 Vが選ばれ、真空管の場合100 Vや50 Vが選ばれることが多かったようである。10の倍数のような、切りのいい数字のほうが演算変数への換算が楽であることは言うまでもない。
3.2 換算係数
一元の常微分方程式の場合、現れる変数は従属変数1つ(以後\(y\)とする)、独立変数1つ(以後\(t\)とする)である。常微分方程式は従属変数の独立変数に関する微分項や独立変数についての関数同士の関係を式で表したものといえる。なかでも、
\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2}+3\frac{\mathrm{d}y}{\mathrm{d}t}+y=0\tag{61}\]
のように、独立変数が陽に現れない(微分記号中にしか現れない)常微分方程式があれば
\[\frac{\mathrm{d}y}{\mathrm{d}t}+t^2y-t+10=0\tag{62}\]
のように独立変数が陽に現れるものもある。(このように独立変数を陽に含む常微分方程式を非自励系/非自律系と呼ぶ。)
結論から申し上げると
- 従属変数
- 陰に現れる独立変数
- 陽に現れる独立変数
の3種類の変数に対してそれぞれ以下の換算係数を定義することになっている。
- 電圧換算係数 (従属変数換算係数)
- 時間換算係数(独立変数時間換算係数)
- 独立変数電圧換算係数
文献によっては、振幅換算係数(Amplitude scaling factor)と呼称されていることもある。文字通り方程式中の従属変数\(y\)を、無次元の演算変数へ変換するための換算係数であり、次のように定義される。
\[a_Y = \frac{Y}{y}\tag{63}\]
つまり、
\[Y=a_Y \cdot{y} ,\quad y=\frac{Y}{a_Y}\tag{64}\]
(原従属変数を\(y\), その演算変数を\(Y\)とする)
定義式から電圧換算係数の単位は \([d.u.]^{-1}\) である。演算変数は無次元であるため、原従属変数が無次元であれば電圧換算係数も無次元となるのが分かるだろう。
演算変数の最大値がマシンユニット以下に収まり、かつできるだけ大きい値になるよう換算係数を定めなければならない。電圧換算係数\(a_{y}\)は、原変数の値域に応じて決定される。すなわち、原変数\(y\)の最大値を\(y_{\mathrm{max}}\)とすれば、
\[a_{Y}\leq \frac{1}{y_{\mathrm{max}}}\tag{65}\]
を満たすもので、かつできる限り大きい数値である必要がある。さらに、計算の都合上できるだけ丸い(キリの良い)数字を選ぶ方が良い。たとえば\(y_{\mathrm{max}}\)=9.4mだと推算できるならば、\(a_{Y}=1/10 =0.1\) [1/m]が望ましい。そうすれば、オシロスコープなどに描かれる解波形の最大値は9.5V(演算変数で0.95)になるはずで、マシンユニットに相当する10Vを超えない。最大値が100N(ニュートン)であるならば、それ自体が丸い数字であるため、\(a_{Y}=1/100=0.01\) 1/Nとしてよいだろう。この場合、オシロコープに表示される最大値の読み取り値は10Vで、演算変数では1となる。
2階以上の微分方程式なら必ず、電圧信号として現れる微分項(\(\frac{\mathrm{d}x}{\mathrm{d}t}\,,\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\,,\cdots\))が存在するので、それらについても\(x\)と同様に電圧換算しなくてはならない。
微分方程式が線形定係数で非同次であるような場合は、電圧換算は初期条件のみ行えばよく、さらに変数\(x\)とその微分項すべてについて電圧換算係数を共通にしても不都合が生じることは少ない。一方、変数係数の場合、強制項を有する場合、非線形微分方程式である場合、もしくは複数の従属変数が出現し複雑なフィードバックが行われるような場合などでは、各微分項についてその最大値がどうなるか吟味し、別個の電圧換算係数を与えることが必要になる可能性が出てくる。例えば、\(x\;,\frac{\mathrm{d}x}{\mathrm{d}t}\;,\frac{\mathrm{d}^2x}{\mathrm{d}t^2}\;\cdots\) に対して、\(\frac{X}{a_{X}}\;,\frac{1}{a_{\dot{X}}}\frac{\mathrm{d}X}{\mathrm{d}t}\;,\frac{1}{a_{\ddot{X}}}\frac{\mathrm{d}^2X}{\mathrm{d}t^2}\;\cdots\)のような換算を行う。
実際の運用では、1元\(n\)階線形常微分方程式であれば、\(n-1\) 階項の値がもっとも先に計算機単位を超えるので、その項の最大値を推算して電圧換算係数を決めるのが手っ取り早い。何となれば、1より大きい角周波数の信号の振幅は、積分器を通過する間にその角周波数に反比例する形で減衰していくからである。あえて超低周波で演算する場合を除けば大抵でこの関係が成り立つので、電圧信号として現れる最大階数項の\(n-1\)階微分項のスケールを調べれば十分であることが多い。
ただし、上記は縦続積分器群の間に信号の「流入」が無い場合のみで成り立つ。積分器の入出力間に乗算器や加算器による外部信号の加乗算がある場合、周波数や振幅の変化が生じるので、各項個別に精査する必要がある。特に非線形方程式の場合は最大値推算が難しいことが多く、トライアンドエラーでスケーリングを行うことになるだろう。
3.2.2 (独立変数)時間換算係数 \(a_\tau\)
時間換算係数(または独立変数時間換算係数)は、原方程式中の独立変数(微分項に現れるものや、\(\sin{\omega{t}},\,,\exp{(kt)}\)内部に現れるものなど、直接電圧として扱わない変数)\(t\)から、演算変数\(\tau\)への換算を与える換算係数で、
\[a_\tau =\frac{\tau}{t}\tag{66}\]
と定義される。すなわち
\[\tau=a_\tau\cdot{t},\quad t=\frac{\tau}{a_\tau}\tag{67}\]
である。前にもふれたように、ギリシャ文字\(\tau\)は式中の陰表的独立変数を時間次元に換算した後の演算変数であることを示すものとする。原独立変数の次元は何でもよいが、アナログコンピュータは独立変数を時間として扱うから、変換先の演算変数の次元は必ず時間である。ゆえに時間換算係数の単位は \([s][i.u.]^-1\)であり、原変数が無次元変数であれば時間換算係数は時間の次元を持つ。
通常は「時間換算係数」という名称を使用するが、後述の「独立変数電圧換算係数\(a_T\)」との対照性に注目するときは「独立変数時間換算係数」と呼ぶこととする。\(a_{\tau}\)と\(a_{T}\)は次元の異なる量であるし、その役割も異なるので混同しないように注意。
時間換算係数の選定は、繰り返し周波数が決まっている高速くりかえし型アナログコンピュータ(演算を数十ミリ秒の周期で繰り返して解波形を繰り返し周期と同期させたオシロスコープの静止画像として得る方式)を用いる場合に特に重要である。高速型を使う場合に限っていうと、
\[a_{\tau}=\frac{[アナログ計算機の演算時間=繰り返し周期]}{[原独立変数の範囲]}\]
が時間換算係数の選定の基準となる。ここで繰り返し周期とは演算モードの時間(演算時間)であり、初期条件モードの時間は含まない。
時間換算係数を1より小さくするほど、時間軸は実時間より圧縮され、解波形の周波数は高くなる。実時間演算を行う場合、\(a_{\tau}=1\)となるのでそのまま\(t\)を\(\tau\)に変えればよい。逆に時間軸を延引して実時間よりゆっくり演算したい場合(XYレコーダなどのペンレコーダに解を記録したい場合など)は1より大きくすればよい。時間換算係数は、時間軸を何倍延引するかの指標である。
時間換算係数を求める関係で2階以上の線形常微分方程式の固有周波数を推算したい場合、特性方程式を解いて複素解の虚部から求める必要がある。微分方程式が安定かどうか(解が発散するか)はRouthの安定判別法を用いて判定できるだろう。
ちなみに、時間換算係数を負の値にとると、各積分器入力(微分値)の正負が逆転し、\(t\)が大きくなるにつれて\(\tau\)が小さくなることになるつまり、演算回路が出力する解は、時間換算係数が正の場合とは逆方向に解が進む。ためしに減衰振動の2階微分方程式の場合で負の時間換算係数\(a_\tau\)=-1を施してみると、もとの方程式の1階微分項の係数の正負を逆転させたものを解くことと同義となることがわかる。実際に演算してみると発散振動解が得られるので興味のある方は確かめてほしい。この技術はNegative time scaling というもので、初期値が不明だが\(t=0\)以外における値が分かっている場合など、境界値問題で有用である。詳しくは文献[10]を参照して頂きたい。
3.2.3 独立変数電圧換算係数 \(a_T\)
この独立変数電圧換算係数は、方程式中に陽表的に現れる独立変数、つまり\(\mathrm{d}/\mathrm{d}t\)のような微分記号として現れるものや、\(\sin\)や\(\exp\)といった時間関数の位相内部に現れるものなどではなく、「はだか」の\(t\)として式中に現れる独立変数を、時間に比例する電圧信号\(T\)に換算する際の換算係数である。
独立変数電圧換算係数\(a_{T}\)は
\[a_T= \frac{T}{t}\tag{68}\]
つまり
\[T=a_{T}\cdot t\quad , \quad t = \frac{T}{a_T}\tag{69}\]
で定義される。\(T\)と前述の\(Y\)はどちらも電圧値であることに注意されたい。この換算係数は時間換算係数と異なり単位は\([MU][i.u.]^-1\)となる。MUは無次元単位なので、全体としては\([i.u.]^-1\)の次元を持つ。ゆえに原独立変数が無次元であれば\(a_T\)も無次元となる。
\(a_{T}\)の値は電圧換算係数と同じように、
\[a_{T} \leq \frac{1}{t_{\mathrm{max}}}\tag{70}\]
を満たし、かつできる限り大きい値を選定する。
ちなみに独立変数電圧換算係数は私が勝手に命名したもので、このような名称が用いられた文献があるわけではない。陽表的に現れる独立変数の換算係数について「時間換算係数」と区別しない書物が多いようである。それどころか、陽に現れる独立変数のスケーリングについて全く言及しない専門書も存在する。
私があえて両者を区別したのは、陽に現れる独立変数と微分記号\(\mathrm{d}/\mathrm{d}t\)に現れる独立変数が全く別種であることを明確にするためである。たとえば、
\[\frac{\mathrm{d}y}{\mathrm{d}t}=t\tag{71}\]
という微分方程式をアナログコンピュータで解析したい場合を考える。この式の左辺の\(t\)と右辺の\(t\)は意味が全く異なることに注意されたい。左辺の\(\mathrm{d}/\mathrm{d}t\)はアナログコンピュータでは真に「時間」として扱う一方、右辺の\(t\)は明らかに電圧信号、正確には「時間に比例する電圧信号」であり、物理量としての時間そのものではない。微分記号に現れる独立変数に対しては (原変数)→(時間)の換算を考えるため、時間換算係数として前項のように定義したが、陽に現れる独立変数については(原変数)→(電圧)の換算を考えないといけない。時間換算係数をそのような\(t\)に適用していいはずがないことが分かるだろう。これが時間換算係数とは別の換算係数\(a_T\)を定義する動機である。
※ \(\exp{(kt)}\)や\(\sin{(\omega{t})}\)内部の\(t\)も微分記号\(\frac{\mathrm{d}}{\mathrm{d}t}\)の\(t\)の扱いに準じるが、それらの時間関数を\(\exp\)や\(\sin\)の関数発生器(出力電圧が入力電圧の関数となる演算器)に時間比例電圧信号を入力して生成する場合は全く話は別であり、その場合は\(\exp{(k\frac{\tau}{a_{\tau}})}\)ではなく、独立変数電圧換算係数を用いて\(\exp{(k\frac{T}{a_T})}\)としなくてはならない。反対に、積分器等を用いて生成する場合は時間換算係数を用いる。
3.3 スケーリング操作の一般化
独立変数を\(t\)、従属変数を\(y\)として、一元常微分方程式は以下の如く表される。
\[ f\left(\;\frac{\mathrm{d}^{n}y}{\mathrm{d}t^n},\frac{\mathrm{d}^{n-1}y}{\mathrm{d}t^{n-1}},\quad...\quad , \frac{\mathrm{d}y}{\mathrm{d}t},y,\quad t^m,t^{m-1},\quad...\quad t^2,t\;\right)=0\tag{72}\]
これを原方程式としてスケーリングを行い演算方程式に直す。従属変数に対しては
\[y=\frac{Y}{a_Y}\tag{73}\]
陰に現れる独立変数に対しては
\[t=\frac{\tau}{a_{\tau}}\tag{74}\]
陽に現れる独立変数に対しては
\[t=\frac{T}{a_{T}}\tag{75}\]
なる代入操作をそれぞれ行えばよろしい。その結果、演算方程式は以下のようになる。
\[ f \left(\;\frac{{a_\tau}^n}{a_Y}\frac{\mathrm{d}^{n}Y}{\mathrm{d}\tau^n},\frac{{a_\tau}^{n-1}}{a_Y}\frac{\mathrm{d}^{n-1}Y}{\mathrm{d}\tau^{n-1}},\quad...\quad , \frac{a_\tau}{a_Y} \frac{\mathrm{d}Y}{\mathrm{d}\tau}, \frac{Y}{a_Y}, \quad \frac{T^m}{{a_T}^m}, \frac{T^{m-1}}{{a_T}^{m-1}} ,\quad ... \quad \frac{T^2}{{a_T}^2},\frac{T}{a_T}\;\right)=0\tag{76}\]
もちろん、上式は非線形微分方程式についても成立する。陽関数法で解くのなら、この変形の後に最高微分階数項\(\frac{\mathrm{d}Y^{n}}{\mathrm{d}\tau^{n}}\)について解いた形に整理し、ブロックダイヤグラムを作成することになる。
各換算係数の具体的数値を代入する前に、まずは文字のまま最高階について整理した後、計算機の線形性が保たれる周波数範囲や係数器の係数設定範囲を加味して換算係数値を決定するのがよい。
3.4 時間比例電圧信号を発生させるときの注意点
独立変数項のべき乗の生成は、1次項を定数の積分により発生させた後、(1)積分器で縦続積分する方法 (2)乗算器で乗じていく方法 の2種がある。
3.4.1 縦続積分による方法
べき乗の係数を考慮すると、独立変数の単項式 \(y_1(t)=t\,,y_2(t)=t^{2}\,,y_3(t)=t^{3}\,,\,...\,,y_{m}(t)=t^{m}\) を得るために必要なm個の積分器それぞれの原方程式は
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}y_1}{\mathrm{d}t}&=&1\\\\\displaystyle\frac{\mathrm{d}y_2}{\mathrm{d}t}&=&2\,y_1=2\,t\\\\\displaystyle\frac{\mathrm{d}y_2}{\mathrm{d}t}&=&6\,y_2=6\,t^{2}\\\\&\vdots\\\\\displaystyle\frac{\mathrm{d}y_m}{\mathrm{d}t}&=&m!\,y_{m-1}=m!\,t^{m-1}\end{cases}\tag{77}\end{eqnarray}
となる。初段積分器で定数1を積分し、傾き1の比例関数を生成した後、次々と積分していく仕組みである。
上の式群は数学的式としては正しいが、このまま演算方程式に直すと間違いが起こる。最初の式の左辺の「1」を通常通りの定数として解釈し演算回路を組むと、マシンユニットが10Vである計算機の場合は積分器入力に1MU=10Vを入力することとなり、電子回路的には傾き1ではなく傾き10の比例信号が出力されることとなる。このつじつま合わせのため、初段積分器入力の定数項は特別扱いし、計算機のマシンユニット電圧 \(V_{MU}\) に依存する換算係数
\[a_{const}=\frac{V_{MU}}{1V}\tag{78}\]
を導入し、右辺定数項を\(a_{const}\) で除すことにする。マシンユニット電圧が10Vの場合、\(a_{const}=10\) である。(77)式を改めて、
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}y_1}{\mathrm{d}t}&=&\displaystyle\frac{1}{a_{const}}\\\\\displaystyle\frac{\mathrm{d}y_2}{\mathrm{d}t}&=&2\,y_1=2\,t\\\\\displaystyle\frac{\mathrm{d}y_2}{\mathrm{d}t}&=&6\,y_2=6\,t^{2}\\\\&\vdots\\\\\displaystyle\frac{\mathrm{d}y_m}{\mathrm{d}t}&=&m!\,y_{m-1}=m!\,t^{m-1}\end{cases}\tag{79}\end{eqnarray}
が最終的な原方程式となる
時間換算係数を \(a_{\tau}\) 、電圧換算係数を \(a_{y_1}\,,a_{y_2}\,,a_{y_3}\,,\,...\,a_{y_m}\) とする。\(a_{y_1}\)は前述した独立変数電圧換算係数 \(a_{T}\) に相当するものであるから、そのことを明示的に示すために \(a_{y_1}=a_{T}\;,a_{y_2}=a_{T^2}\;,a_{y_3}=a_{T^3}\;,\;...\;a_{y_m}=a_{T^m}\) と表記しなおそう。 電圧換算係数同士の関係については、例えば1MUとして\(T=5\)を対応させたい場合、\(a_{y_1}=1/5\;,a_{y_2}=1/25\;,a_{y_3}=1/125\;...\;,a_{y_m}=1/5^{m}\) のようにべき乗の関係が成り立つよう定めればよい。なので、最初から電圧換算係数としては \(a_{T}\) のみ用意し、演算方程式に直す。
\begin{eqnarray}\begin{cases}\displaystyle\frac{a_{\tau}}{a_{T}}\frac{\mathrm{d}Y_1}{\mathrm{d}\tau}&=&\displaystyle\frac{1}{a_{const}}\\\\\displaystyle\frac{a_{\tau}}{{a_{T}}^2}\frac{\mathrm{d}Y_2}{\mathrm{d}\tau}&=&\displaystyle2\,\frac{T}{a_{T}}\\\\\displaystyle\frac{a_{\tau}}{{a_{T}}^3}\frac{\mathrm{d}Y_3}{\mathrm{d}\tau}&=&\displaystyle 6\,\frac{T^{2}}{{a_{T}}^2}\\\\&\vdots\\\\\displaystyle\frac{a_{\tau}}{{a_{T}}^m}\frac{\mathrm{d}Y_m}{\mathrm{d}\tau}&=&\displaystyle m!\,\frac{T^{m-1}}{{a_T}^{m}}\end{cases}\tag{78}\end{eqnarray}
すなわち
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}Y_1}{\mathrm{d}\tau}&=&\displaystyle\frac{a_{T}}{a_{\tau}\,a_{const}}\\\\\displaystyle\frac{\mathrm{d}Y_2}{\mathrm{d}\tau}&=&\displaystyle 2\,\frac{\,a_{T}}{a_{\tau}}\,T\\\\\displaystyle\frac{\mathrm{d}Y_3}{\mathrm{d}\tau}&=&\displaystyle 6\,\frac{a_{T}}{a_{\tau}}\,T^2\\\\&\vdots\\\\\displaystyle\frac{\mathrm{d}Y_m}{\mathrm{d}\tau}&=&\displaystyle m!\,\frac{a_{T}}{a_\tau}\,T^{m-1}\end{cases}\tag{79}\end{eqnarray}
このようなスケーリングを施せば、換算係数を無用に増やさずスマートに演算方程式を表せる。
3.4.2 積分器と乗算器を用いる方法
1次項の生成は 3.4.1 の方法と同じだが、2次項以上は乗算器による変数乗算で次々と実現する場合は、通常の従属変数の乗算と同様、その出力は延々にスケーリングされた演算変数である。1次項が1MUを超えないようスケーリングしさえすれば、乗算器出力のスケーリングについては考えなくてよい。電子式アナログ乗算器の出力は、普通は2入力変数の積を10Vで除した値となっており、入力が10V(1MU)を超えない限り出力も10Vを超えないからである。
積分器の個数に余裕がないが、乗算器は余っている場合はこの方法を使うと良い。(演算誤差の累積には十分注意されたい。)
3.4.1, 3.4.2の両手法を演算回路に落とし込むと、以下の図のようになる。ただし、マシンユニット電圧が10Vのアナログコンピュータを用いた場合を考えている。
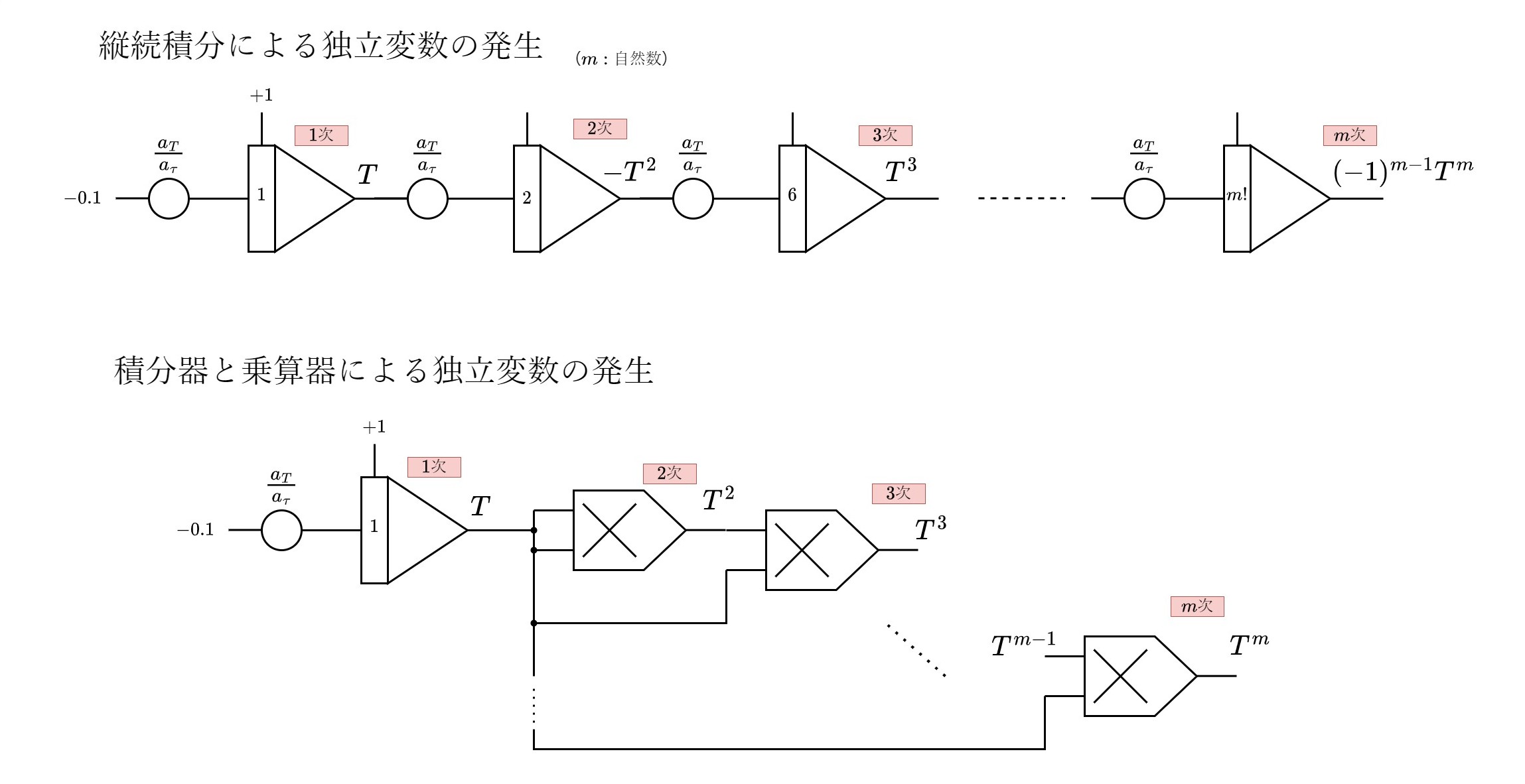
両手法ともに共通の換算係数を用いることができる。(ただし、積分器を用いる場合は時間換算係数に留意すること。)
独立変数が陽に現れる微分方程式のスケーリング例として、
\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2}+\left(t^3+t\right)y=0\tag{80}\]
を演算方程式に直すことを考えよう。
\[a_{\tau}\frac{\mathrm{d}^2Y}{\mathrm{d}\tau^2}+\left(\frac{T^3}{{a_{T}}^3}+\frac{T}{a_{T}}\right)Y=0\tag{81}\]
となるわけだが、演算信号\(T\) や \(T^{3}\)としては上記方法における乗算器や積分器出力そのままを用いればよいことになる。\(1/a_{T}\) などの換算係数が1より小さい場合は係数器で設定し、1より大の場合は他線形演算器の入力ゲインをうまく用いるか別個にスケーリングする。
3.5 演算変数から原変数へ
アナログコンピュータで計算を実行した後、オシロスコープやペンレコーダから得られた電圧値から原変数換算値を得たいときは、スケーリングと逆の操作を行えばいい。
たとえば、解関数の最大値として9Vという電圧値を読み取ったとする。これは演算変数値で0.9(MU)なので、原変数相当値はこれを電圧換算係数で除した値\(\frac{0.9}{a_Y}\)となる。
これまで述べたスケーリングの方針を図に表した(下図)。変数換算はもっとも躓きやすいところであるが、各々の換算について、なぜその操作を行う必要があるのかを常に考えておけば間違うことは無いだろう。
3.5 プログラム例
以上の説明で換算係数の設定方法は了解されたと思う。スケーリングの理解をさらに深化させるため、今度は原方程式と換算係数から演算方程式を立ててブロックダイヤグラムを組むところまでの一連の流れを簡単な例を用いて説明する。
3.5.1 《例題1》
\[\frac{\mathrm{d}^{2}y}{\mathrm{d}t^2}+40\frac{\mathrm{d}y}{\mathrm{d}t}+300y=0\tag{82}\]
という2階線形微分方程式を解くことを考える。yの最大値を10とすると、電圧換算係数 \(a_{y}\)=0.1 と定まる。また、高速型のアナログコンピュータを用いるものとし、繰り返し周期10msで\(0\leq t \leq 1\)の範囲の解をオシロスコープで観察したいとすれば、時間換算係数\(a_{\tau}\)は\(10^{-2}\)と定まる。以上を踏まえ、式中の \(y, t\)を演算変数 \(Y, \tau\)に変換する。
\[t=\frac{\tau}{a_{\tau}}, \qquad y=\frac{Y}{a_{Y}}\tag{83}\]
から、各項は
\[\frac{\mathrm{d}^{2}y}{\mathrm{d}t^2}=\frac{a_{t}^{2}}{a_{Y}} \cdot \frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^{2}}=\frac{10^{-4}}{10^{-1}}\cdot \frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^{2}}=10^{-3} \frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^{2}}\tag{84}\]
\[\frac{\mathrm{d}y}{\mathrm{d}t}=\frac{a_{\tau}}{a_{Y}} \cdot \frac{\mathrm{d}Y}{\mathrm{d}\tau}=\frac{10^{-2}}{10^{-1}}\cdot \frac{\mathrm{d}Y}{\mathrm{d}\tau}=10^{-1} \frac{\mathrm{d}Y}{\mathrm{d}\tau}\tag{85}\]
\[y=\frac{1}{a_{Y}}\cdot Y=\frac{1}{10^{-1}}Y=10Y\tag{86}\]
であり、演算方程式は、
\[10^{-3}\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}+4 \frac{\mathrm{d}Y}{\mathrm{d}\tau}+3\times 10^{3} Y=0\tag{87}\]
となる。
まじめに計算するとき手順は上の通りなのだが、斉次線形常微分方程式では電圧換算係数が全項にわたり\(-1\)次であり、全て払えるので考えなくてよい。つまり、最初から
\[a_{\tau}^{2}\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}+40a_{\tau} \frac{\mathrm{d}Y}{\mathrm{d}\tau}+3\times 10^{2}Y=0\tag{88}\]
すなわち
\[10^{-4}\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}+0.4 \frac{\mathrm{d}Y}{\mathrm{d}\tau}+3\times 10^{2}Y=0\tag{89}\]
のように、\(a_{t}\)のみを考えればよい。斉次線形微分方程式であり、一階微分の初期条件が0であるから、電圧換算係数は\(y\)の初期条件のみに依存する。\(y\)の初期条件の大きさが1MUより小さくなるようスケーリングしておきさえすれば演算方程式への変換作業では最初から時間換算係数のみを考えるだけでいいので楽であろう。
これを陽関数法で解く場合、(89)を2階微分項について整理するわけだが、注意が必要なのが各微分項の係数である。これらはむやみに払わず、\(n\)階微分項の係数は積分時定数\(RC\)の\(n\)乗を常に残すようにする。低速型(R=1MΩ, C=1μF)のときはRC=1sなので考慮する必要はないが、今回のように高速型の時は十分注意すべきである。たとえばR=1MΩ, C=1nFのとき積分時定数が\(10^{-3}\)であることに注意して(89)を変形すると、
\[10^{2}\cdot \Bigl(10^{-6}\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}\Bigr)=-4\times10^{2}\cdot \Bigl(10^{-3} \frac{\mathrm{d}Y}{\mathrm{d}\tau}\Bigr)-3\times 10^{2}Y\tag{90}\]
整理して
\[ \Bigl(10^{-6}\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}\Bigr)=-4 \Bigl(10^{-3} \frac{\mathrm{d}Y}{\mathrm{d}\tau}\Bigl)-3Y\tag{91}\]
となる。
その理由を説明しよう。積分器出力は一般に
\[e_{out}=-\frac{1}{RC}\int e_{in}\mathrm{d}t\tag{92}\]
つまり、
\[e_{in}=-RC \frac{\mathrm{d}}{\mathrm{d}t} e_{out}\tag{93}\]
で表される。(簡単のため積分初期条件は考慮していない。) 高速型でC=1nFのとき時定数は\(10^{-3}\)sとなる。その場合、2個の積分器を縦続接続し、2段目の出力を\(x\)としたとき、1段目の出力は\(10^{-3}\cdot \mathrm{d}x/\mathrm{d}t\)、1段目の入力は\(10^{-6} \cdot \mathrm{d}^{2}x/\mathrm{d}t^{2}\)で表される。つまり、積分時定数が高速型積分器の直列接続の数だけ累乗されて行く。このようなゲインは積分器の内部で発生するもので、係数器などで別途設定するものではないため、ブロックダイヤグラムを組むときに考慮する必要はない。したがって、高速型では(91)式のように項の階数に応じた積分器時定数と微分項を一体としてまとめ、積分器以外の他の演算器で考慮する必要のない値であることを明確にする。
もし、同じ方程式を低速型と高速型両方で調査したくて、用いる計算機に積分器時定数切り替え機能がある場合
\[\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}=-4 \frac{\mathrm{d}Y}{\mathrm{d}\tau}-3Y\tag{94}\]
といった風に積分器時定数を省略して記述してもよいだろう。というのも、低速型であろうが高速型であろうが、上式を演算回路として実装しさえすれば、あとは積分コンデンサの切り替えだけで時間換算係数が勝手に置き換わる(例えば1μFから1nFへ切り替え、時定数を1/1000にするだけで\(a_\tau\)は1000倍になる)からである。係数器の値を変える必要など全くない。
具体的な例とともに示した方が分かりやすいかもしれない。低速型で時間換算係数、電圧換算係数がともに1のとき、本例題の式
\[\frac{\mathrm{d}^{2}y}{\mathrm{d}t^2}+40\frac{\mathrm{d}y}{\mathrm{d}t}+300y=0\tag{95}\]
の演算方程式は
\[\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}+40\frac{\mathrm{d}Y}{\mathrm{d}\tau}+300Y=0\tag{96}\]
となる。このとき演算回路内の全積分器のコンデンサがC=1μFであるとする。これを1nFに変更して時定数を1/1000倍にするとn階微分項を入力とする積分器は\(1000^n\)倍のゲインを持つことになるため、
\[10^{-6}\frac{\mathrm{d}^{2}Y}{\mathrm{d}\tau^2}+40\cdot 10^{-3}\frac{\mathrm{d}Y}{\mathrm{d}\tau}+300Y=0\tag{97}\]
これは原方程式において時間換算係数を1/1000としたときの演算方程式と一致している。
「全積分器の時定数を等しくn倍したら、方程式の時間換算係数を1/n倍したことになる」
ということは覚えておいて損はないだろう。
さて、求めた演算方程式ブロックダイヤグラムは以下の通りになる。積分器などの「1」入力端子は1MΩの入力抵抗値(C=1μFの場合ゲインが1倍になる端子である)、「10」入力端子は100kΩの入力抵抗値(同じくゲインが10倍になる端子という意味)であることを示し、すべての積分器は時定数が1msであるとする。
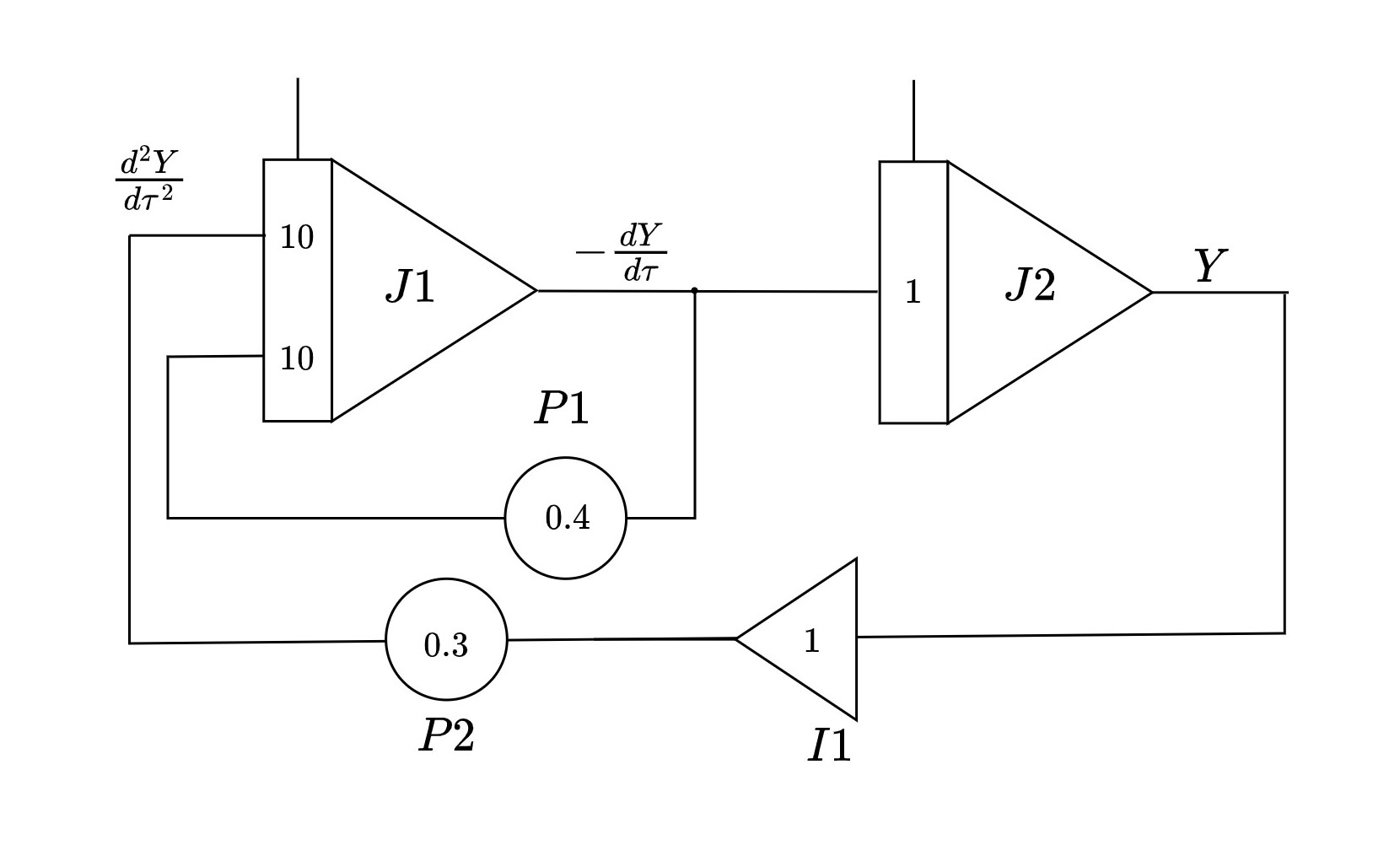 上のブロックダイヤグラムは一例に過ぎない。一番右の信号を\(Y\)ではなく\(-Y\)と置けば、\(\mathrm{d}Y/\mathrm{d}\tau , -\mathrm{d}Y^{2} / \mathrm{d}\tau^2\)のように各変数の符号が逆転するだけで、ダイヤグラム自体は変わらない。時定数が1 msであるから、\(-\mathrm{d}Y/\mathrm{d}\tau\)は\(-10^{3}\mathrm{d}Y/\mathrm{d}\tau\)、\(\mathrm{d}Y^{2} / \mathrm{d}\tau^2\)は\(10^{6}\mathrm{d}Y^{2} / \mathrm{d}\tau^2\)を意味することに注意。反転器 I1のゲインを10にできるなら、その入力先をJ1のゲイン1入力端子としてもよい。また、(係数器の負荷効果を無視すれば)反転器と係数器の位置はどちらが先でも同じである。
上のブロックダイヤグラムは一例に過ぎない。一番右の信号を\(Y\)ではなく\(-Y\)と置けば、\(\mathrm{d}Y/\mathrm{d}\tau , -\mathrm{d}Y^{2} / \mathrm{d}\tau^2\)のように各変数の符号が逆転するだけで、ダイヤグラム自体は変わらない。時定数が1 msであるから、\(-\mathrm{d}Y/\mathrm{d}\tau\)は\(-10^{3}\mathrm{d}Y/\mathrm{d}\tau\)、\(\mathrm{d}Y^{2} / \mathrm{d}\tau^2\)は\(10^{6}\mathrm{d}Y^{2} / \mathrm{d}\tau^2\)を意味することに注意。反転器 I1のゲインを10にできるなら、その入力先をJ1のゲイン1入力端子としてもよい。また、(係数器の負荷効果を無視すれば)反転器と係数器の位置はどちらが先でも同じである。
今回は初期条件の存在を無視したが、実際に微分方程式を解く場合、非零の初期条件に対しては電圧換算を行わねばならないことに注意して欲しい。
3.5.2 《例題2》
非線形微分方程式
\[\frac{\mathrm{d}^{2}x}{\mathrm{d}t^2}+3\frac{\mathrm{d}x}{\mathrm{d}t}+x+x^{3}=0\tag{98}\]
を、初期条件 \(x(0)=-2\quad{,}{x'(0)=2}\) のもとで解く。注意すべきは、\(x\)と\(\frac{\mathrm{d}x}{\mathrm{d}t}\) の換算係数を安易に共通させないようにすることである。解が減衰的であることは分かっても、最大値=初期条件とは限らないからである。このように、電圧信号として現れる微分項のスケールが不明な場合は、それらを新たな従属変数として扱い、式を1階連立微分方程式に直してからきちんとスケール換算を行うことをお勧めする。(その際の電圧換算係数の選定は試行錯誤的におこなってよい。)
2階微分方程式であるから2元1階常微分方程式に直す。
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}=&y\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=&-3y-x-x^{3}\end{cases}\tag{99}\end{eqnarray}
\(x\)と\(y\)をスケーリングして1MU以下の信号(演算信号)に置き直しさえすれば、3乗項\(X^{3}\)も自動的に1MU以下になる。
演算方程式は、
\begin{eqnarray}\begin{cases}\displaystyle\frac{a_{\tau}}{a_{X}}\frac{\mathrm{d}X}{\mathrm{d}\tau}=&\displaystyle\frac{Y}{a_{Y}}\\\\\displaystyle\frac{a_{\tau}}{a_{Y}}\frac{\mathrm{d}Y}{\mathrm{d}{\tau}}=&\displaystyle{-3\frac{Y}{a_Y}-\frac{X}{a_{X}}-\frac{X^3}{{a_{X}}^{3}}}\end{cases}\tag{100}\end{eqnarray}
推算若しくは試行により、\(x\)の換算係数\(a_X\)として1/2を、\(y={\mathrm{d}x}/{\mathrm{d}t}\)の換算係数 \(a_Y\) として1/4を選んだとする。
低速モード(\(a_{\tau}=1\))の場合の最終的な演算方程式は
\begin{eqnarray}\begin{cases}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=&2Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}{\tau}}=&{-3{Y}-0.5X-2X^3}\end{cases}\tag{101}\end{eqnarray}
ブロックダイヤグラムは省略するが、例題1と同様に陽関数法を用いて容易に構成できる。
参考までに、原方程式の厳密解のグラフを示しておく。
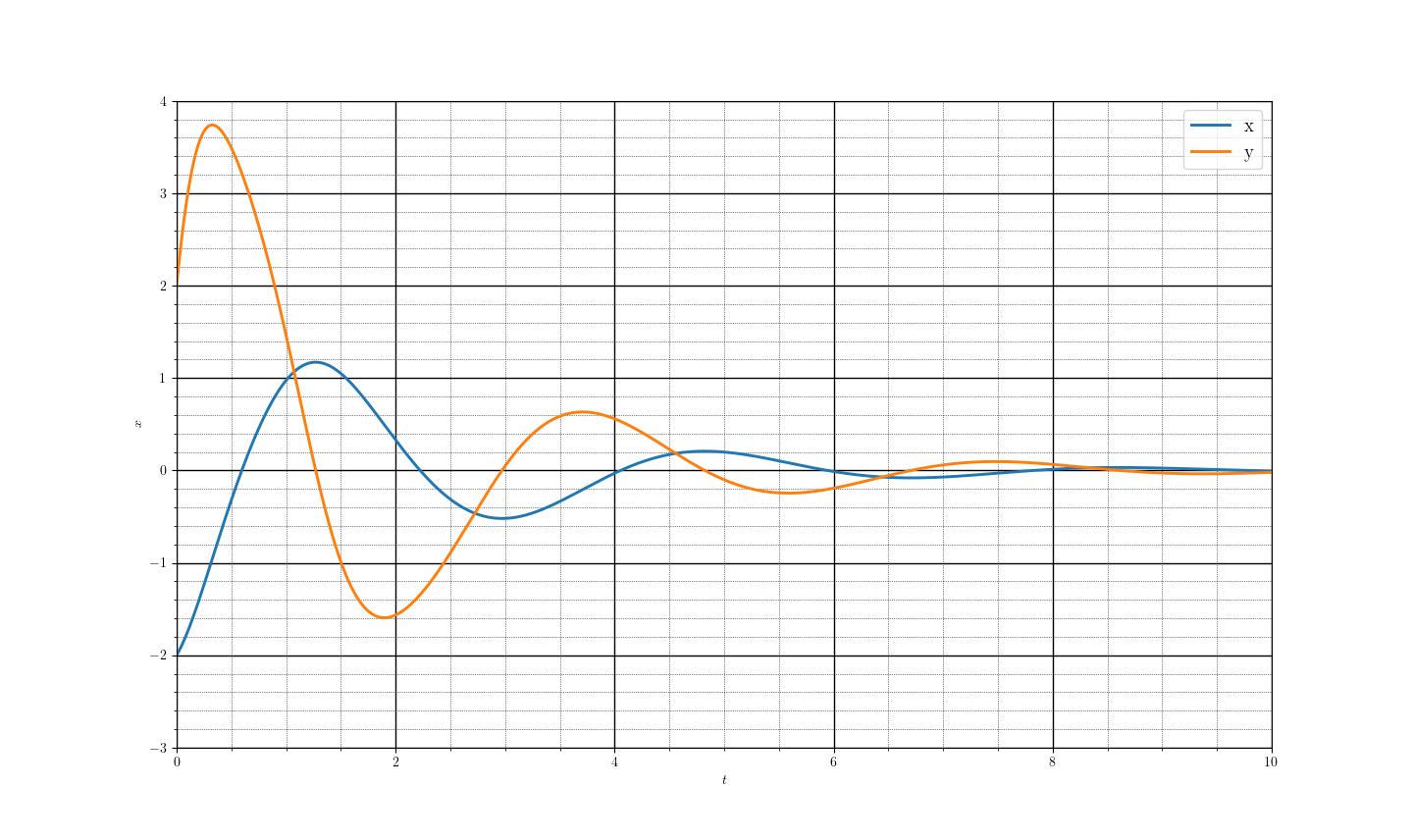
\(\frac{\mathrm{d}^{2}x}{\mathrm{d}t^2}+3\frac{\mathrm{d}x}{\mathrm{d}t}+x+x^{3}=0\)の解のグラフ
4. 参考文献
[1] 野村民也, 三浦武雄. 「アナログ電子計算機」 コロナ社, 1960.
[2] 藤田広一. 「アナログ計算機のプログラム」昭晃堂,1978.
[3] 若山芳三郎, 稲垣幸一. 「新訂入門アナログ計算機」 啓学出版,1976 .
[4] 三浦武雄. 「アナログ計算機のソフトウェア」 コロナ社.
[5] J.Robert Ashley. Introduction to Analog Computation. John Wiley and Sons, Inc.
[6] Granino A. korn & Theresa M. Korn. Electronic Analog And Hybrid Computers. McGraw-Hill Book Company, 1964.
[7] 山下英夫. 「電子計算機 アナログ計算機編」オーム社, 1959.
[8] Albert S. Jackson. Analog Computation. McGraw-Hill Book Company, 1960
[9] Kazuo Kurokawa, Ikuo Matsuda. Setup system in analog computer. US Patent 3652843A. Mar. 28, 1972. https://patents.google.com/patent/US3652843
[10] C.R. Hall, S.J. Kahne. "An improved method for analog computer scaling, Mathematics and Computers in Simulation," Volume 12, Issue 1,1970, PP 27-32.
 引用元:
引用元: