第1種ケルビン関数
目次
1.準備
変数をフェーザ表示したラプラス方程式を円筒座標系で変数分離した式として、次のような形の0次のベッセル微分方程式が出現することがある。
\[\frac{\mathrm{d}^2y}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}y}{\mathrm{d}x}-ik^{2}y=0\tag{1}\]
（ただし、\(i\)は虚数単位。）
例えば円筒導体の電流密度などが上式を満たす。（詳しくは表皮効果の導出）
変数変換を行い、式(1)の解関数を0次の第1種ベッセル関数と第2種ベッセル関数を用いて表すと
\[y(x)=C_0\,J_{0}(\sqrt{-i}kx)+C_1\,N_{0}(\sqrt{-i}kx)\quad{(C_0,C_1:定数)}\tag{2}\]
という形になることが知られている。しかし、アナログコンピュータにおいては \(y(x)\) をベッセル関数に基づいて直接解くことはできない。なぜなら、ベッセル関数の返す値は複素数であり、実部と虚部の関数を解析的な形で分離することはできないからである。そもそも
\[\sqrt{-i}=e^{\frac{3}{4}\pi{i}}\tag{3}\]
であるから、変数自体が複素数となっている。
(1)の微分方程式の基本解のうち、原点で正則なほうの複素関数の実部を \(\mathrm{ber}(kx)\)、虚部を \(\mathrm{bei}(kx)\)として、(0次の)第1種ケルビン関数と呼ぶ。
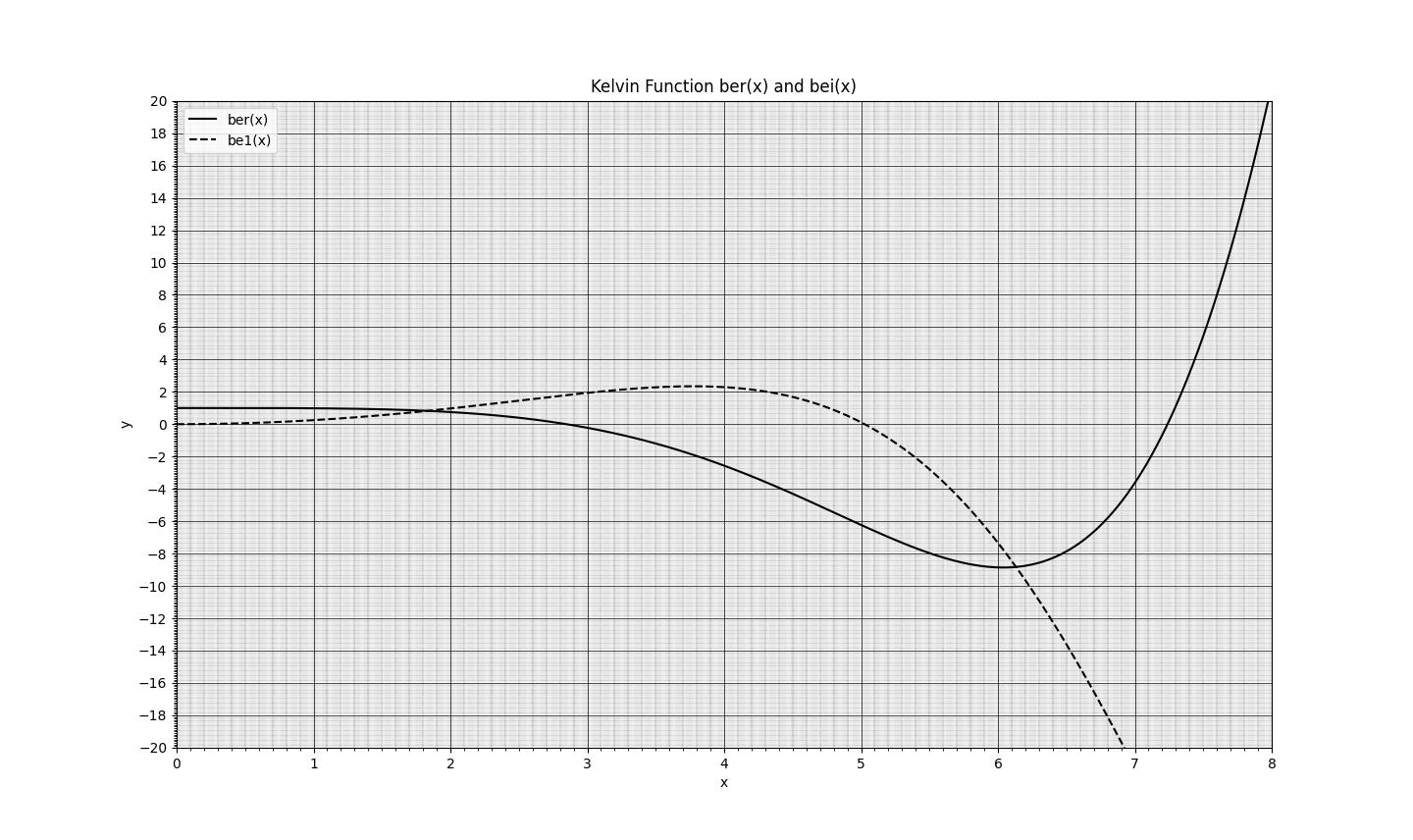
図1 第1種ケルビン関数のグラフ
William Thomson, 1st Baron Kelvin の名からつけられた名前であるのだが、彼は、アナログコンピュータの祖とも言うべき微分解析機の積分機構や、フィードバックにより微分方程式を解くアイデアを考案したあのケルビン卿(Load Kelvin)その人である。
\(0\) 次第1種ベッセル関数との関係は、
\[J_{0}\left(\sqrt{-i}z\right)=J_{0}\left(e^{i\frac{3\pi}{4}}z\right)=\mathrm{ber}(z)+i\mathrm{bei}(z)\tag{4}\]
であるので、(1)式の解の実部と虚部を容易に表せる。
ただ実部の関数と虚部の関数に新たな名を付けただけではあるのだが、ケルビン関数を用いると、アナログコンピュータで(1)式の実部と虚部を別々に求めることができる。要は、\(\mathrm{ber}\) と \(\mathrm{bei}\) が満たす実変数・実係数の微分方程式を演算回路として組めばいい。
まず、(1)の解を実部と虚部に分ける。
\[y(x)=u(x)+iv(x)\tag{5}\]
(5)を(1)に代入すると、実部と虚部それぞれの微分方程式が作れる。
\[\left\{\begin{array}{ll}\displaystyle\frac{\mathrm{d}^2u}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}u}{\mathrm{d}x}=\displaystyle{-v}\\\\\displaystyle\frac{\mathrm{d}^2v}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}v}{\mathrm{d}x}=\displaystyle{u}\end{array}\right.\tag{6}\]
上記の連立微分方程式を根気強く変形し整理していくと、\(v(x)\) のみの高階1元微分方程式に直せる。
\begin{eqnarray}\frac{\mathrm{d}^2}{\mathrm{d}x^2}\left(\frac{\mathrm{d}^2v}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}v}{\mathrm{d}x}\right)+\frac{1}{x}\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\mathrm{d}^2v}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}v}{\mathrm{d}x}\right)&=&-v\\\\\frac{\mathrm{d}}{\mathrm{d}x}\left\{\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\mathrm{d}^2v}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}v}{\mathrm{d}x}\right)\right\}+\frac{1}{x}\left\{\frac{\mathrm{d}^3v}{\mathrm{d}x^3}+\frac{1}{x^2}\left(x\frac{\mathrm{d}^2v}{\mathrm{d}x^2}-\frac{\mathrm{d}v}{\mathrm{d}x}\right)\right\}&=&-v\\\\\frac{\mathrm{d}}{\mathrm{d}x}\left\{\frac{\mathrm{d}^3v}{\mathrm{d}x^3}+\frac{1}{x^2}\left(x\frac{\mathrm{d}^2v}{\mathrm{d}x^2}-\frac{\mathrm{d}v}{\mathrm{d}x}\right)\right\}+\frac{1}{x}\frac{\mathrm{d}^3v}{\mathrm{d}x^3}+\frac{1}{x^2}\frac{\mathrm{d}^2v}{\mathrm{d}x^2}-\frac{1}{x^3}\frac{\mathrm{d}v}{\mathrm{d}x}&=&-v\\\\\frac{\mathrm{d}^4v}{\mathrm{d}x^4}+\frac{1}{x^2}\left(\frac{\mathrm{d}^2v}{\mathrm{d}x^2}+x\,\frac{\mathrm{d}^3v}{\mathrm{d}x^3}-\frac{\mathrm{d}^2v}{\mathrm{d}x^2}\right)-\frac{2}{x^3}\left(x\,\frac{\mathrm{d}^2v}{\mathrm{d}x^2}-\frac{\mathrm{d}v}{\mathrm{d}x}\right)+\frac{1}{x}\frac{\mathrm{d}^3v}{\mathrm{d}x^3}+\frac{1}{x^2}\frac{\mathrm{d}^2v}{\mathrm{d}x^2}-\frac{1}{x^3}\frac{\mathrm{d}v}{\mathrm{d}x}&=&-v\\\\\frac{\mathrm{d}^4v}{\mathrm{d}x^4}+\frac{2}{x}\frac{\mathrm{d}^3v}{\mathrm{d}x^3}-\frac{1}{x^2}\frac{\mathrm{d}^2v}{\mathrm{d}x^2}+\frac{1}{x^3}\frac{\mathrm{d}v}{\mathrm{d}x}+v&=&0\tag{7}\end{eqnarray}
\(u\) についても(7)と同じ形の式が導き出されるので、\(\mathrm{ber}(x),\,\mathrm{bei}(x)\) はどちらも4階微分方程式(7)を満たすことがわかる。
2.アナログコンピュータプログラム
2.1 演算方程式
ここで、(7)式を \(x\) を従属変数、\(t\) を独立変数として書き改める。
\begin{eqnarray}\frac{\mathrm{d}^4x}{\mathrm{d}t^4}+\frac{2}{t}\frac{\mathrm{d}^3x}{\mathrm{d}t^3}-\frac{1}{t^2}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\frac{1}{t^3}\frac{\mathrm{d}x}{\mathrm{d}t}+x&=&0\\\\t^3\,\frac{\mathrm{d}^4x}{\mathrm{d}t^4}+2\,t^2\,\frac{\mathrm{d}^3x}{\mathrm{d}t^3}-t\,\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\frac{\mathrm{d}x}{\mathrm{d}t}+t^3\,x&=&0\tag{8}\end{eqnarray}
(8)を解いて\(x=\mathrm{ber}(t)\) を生成する方法を考えよう。通常の陽関数法では、どう式変形しても右辺に信号飽和の原因となる \(t\) の除算が現れてしまう。ゆえに、高階微分のダミー変数を置くことで除算を回避する。つまり、演算増幅器のオープンループゲインを \(\mu\) として、
\[t^3\,\frac{\mathrm{d}^4x}{\mathrm{d}t^4}+2\,t^2\,\frac{\mathrm{d}^3x}{\mathrm{d}t^3}-t\,\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\frac{\mathrm{d}x}{\mathrm{d}t}+t^3\,x=-\frac{1}{\mu}\frac{\mathrm{d}^5x}{\mathrm{d}t^5}\tag{9}\]
をもとに演算回路を構成すればいい。(ダミー変数法については「演算の理論」を参照) ちなみに各初期条件は、
\[x(0)=1,\;x'(0)=x''(0)=x'''(0)=0,\;x^{(4)}(0)=-\frac{3}{8}\tag{10}\]
である。式(9)をスケーリングするため、以下のように6元1階連立微分方程式に直す。
\[\left\{\begin{array}{llllll}\displaystyle\frac{\mathrm{d}x}{\mathrm{d}t}=y\\\\\displaystyle\frac{\mathrm{d}y}{\mathrm{d}t}=z\\\\\displaystyle\frac{\mathrm{d}z}{\mathrm{d}t}=u\\\\\displaystyle\frac{\mathrm{d}u}{\mathrm{d}t}=v\\\\\displaystyle\frac{\mathrm{d}v}{\mathrm{d}t}=w\\\\\displaystyle{\frac{1}{\mu}\,w}=-y+t\,z-2t^2\,u-t^3\,(x+v)\end{array}\right.\tag{11}\]
\(0\leq{t}\leq{8}\) の間の解を得るとすると、独立変数の電圧換算係数は
\[a_{T}=\frac{1}{8}\tag{12}\]
とすればよい。従属変数の各換算係数は数値計算による概算により
\[a_{X}=\frac{1}{20}\,,a_{Y}=\frac{1}{40}\,,a_{Z}=\frac{1}{30}\,,a_{U}=\frac{1}{15}\,,a_{V}=\frac{1}{20}\,,a_{W}=\frac{1}{20}\tag{13}\]
と定めた。時間換算係数を1として無視すれば、演算方程式は次のようになる。
\[\left\{\begin{array}{llllll}\displaystyle\frac{\mathrm{dX}}{\mathrm{d}\tau}=\frac{a_X}{a_Y}Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\frac{a_Y}{a_Z}Z\\\\\displaystyle\frac{\mathrm{d}Z}{\mathrm{d}\tau}=\frac{a_Z}{a_U}U\\\\\displaystyle\frac{\mathrm{d}U}{\mathrm{d}\tau}=\frac{a_U}{a_V}V\\\\\displaystyle\frac{\mathrm{d}V}{\mathrm{d}\tau}=\frac{a_V}{a_W}W\\\\\displaystyle{\frac{1}{\mu}\,W}=-\frac{a_W}{a_Y}Y+\frac{a_W}{{a_T}a_Z}\,T\,Z-2\frac{a_W}{{a_T}^2 a_U}T^2\,U-\frac{a_W}{{a_T}^3}T^3\,\left(\frac{X}{a_X}+\frac{V}{a_V}\right)\end{array}\right.\tag{11}\]
値を代入して整理すると以下を得る。
\[\left\{\begin{array}{llllll}\displaystyle\frac{\mathrm{d}X}{\mathrm{d}\tau}=2Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\frac{3}{4}Z\\\\\displaystyle\frac{\mathrm{d}Z}{\mathrm{d}\tau}=\frac{1}{2}U\\\\\displaystyle\frac{\mathrm{d}U}{\mathrm{d}\tau}=\frac{4}{3}V\\\\\displaystyle\frac{\mathrm{d}V}{\mathrm{d}\tau}=W\\\\\displaystyle{\frac{1}{\mu}\,W}=-2Y+12\,T\,Z-96\,T^2\,U-512\,T^3\,\left(X+V\right)\end{array}\right.\tag{12}\]
初期条件も忘れずにスケーリングすること。
\[X(0)=0.05,\;Y(0)=Z(0)=U(0)=0,\;V(0)=-0.01875\tag{13}\]
\(\mathrm{bei}(t)\) についても同じ微分方程式を異なる初期条件で解けばいいのだが、回路をもう1セット組むには積分器が足りない。せっかく \(\mathrm{ber}(t)\) が(12)式で得られるのだから、それを強制項として導入した以下の関係式
\[-\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\frac{1}{t}\frac{\mathrm{d}x}{\mathrm{d}t}+\mathrm{ber}(t)=0\tag{14}\]
を利用して \(x=\mathrm{bei}(t)\) を生成すれば、演算器の数を少なく抑えることができるうえ、\(\mathrm{ber}(x)\) と \(\mathrm{bei}(x)\) を同時に得ることができる。\(x=\mathrm{bei}\) の初期条件としては、2階微分項にのみ非零の初期条件 0.5 が必要である。
\(\mathrm{ber}(t)\)の時と同様に高階ダミー変数を導入すると
\[-t\,\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\frac{\mathrm{d}x}{\mathrm{d}t}+t\,\mathrm{ber}(t)=\frac{1}{\mu}\frac{\mathrm{d}^3x}{\mathrm{d}t^3}\tag{14}\]
こんどは元が奇数階なのでダミー変数の符号は正に取った。時間換算係数 \(a_{\tau}=1\) として、\(\mathrm{bei}(t)\) の各微分項を改めて文字でおいて連立微分方程式に直すと、
\[\left\{\begin{array}{llllll}\displaystyle\frac{\mathrm{dX}}{\mathrm{d}\tau}=\frac{a_X}{a_Y}Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\frac{a_Y}{a_Z}Z\\\\\displaystyle\frac{\mathrm{d}Z}{\mathrm{d}\tau}=\frac{a_Z}{a_U}U\\\\\displaystyle\frac{U}{\mu}=-\frac{a_U}{a_Z\,a_T}\,TZ+\frac{a_U}{a_Y}\,Y+\frac{a_U}{a_{Ber}\,a_T}\,T\,{\mathrm{Ber}}\end{array}\right.\tag{16}\]
各換算係数を
\[a_{X}=\frac{1}{40}\,,a_{Y}=\frac{1}{20}\,,a_{Z}=\frac{1}{20}\,,a_{U}=\frac{1}{40}\,,a_{Ber}=\frac{1}{20}\,,a_{T}=\frac{1}{8}\tag{17}\]
とすると、
\[\left\{\begin{array}{llllll}\displaystyle\frac{\mathrm{dX}}{\mathrm{d}\tau}=\frac{1}{2}Y\\\\\displaystyle\frac{\mathrm{d}Y}{\mathrm{d}\tau}=Z\\\\\displaystyle\frac{\mathrm{d}Z}{\mathrm{d}\tau}=2\,U\\\\\displaystyle\frac{U}{\mu}=-4\,TZ+0.5\,Y+4\,T\,{\mathrm{Ber}}\end{array}\right.\tag{18}\]
2.2 ブロックダイヤグラム
(12)および(18)式を実現するブロックダイヤグラムが図2である。
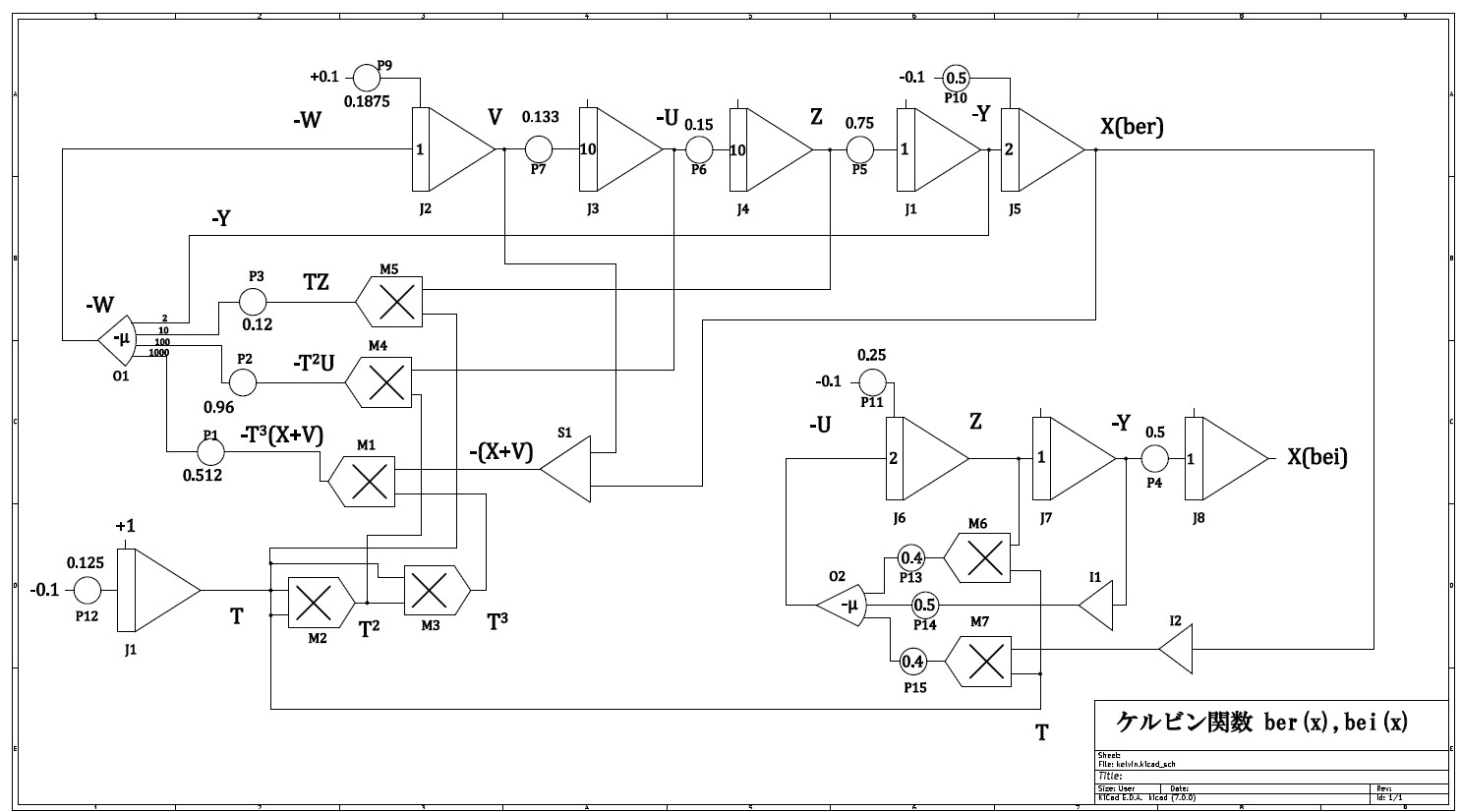
図2 ブロックダイヤグラム
オープンアンプ(O1)の入力端子のゲインに注意。100倍端子や1000倍端子は、それぞれ加算電流入力端子（サミングジャンクション）に10kΩ、1kΩの抵抗を介して接続させることにより実現している。
また、\(\mathrm{ber}(x)\) の演算回路中のマイナーループの中に含まれる符号反転性演算器（積分器、加算器、反転器）の数を数えると、すべて奇数になっていることがわかる。これによりオープンアンプの負帰還動作が保証され、安定な演算が可能になる。これこそが、式(9)において、5階微分項に相当するダミー変数の符号として負を選んだ理由である。もし正を選んでいたら、ループ内で符号反転が偶数回続くことになり、正帰還動作となって安定して解を求めることができない。このように、数学的に正しい式であっても、全てがアナログ計算機で解けるとは限らないので、ダミー変数法を用いて微分方程式を解く場合はダミー変数の符号の取り方に注意するべきである。 元のn階微分方程式が偶数階であれば、ダミー変数（n+1階微分項）の符号は負に、奇数階であれば正にとるのが基本だが、例外もあるので、ブロックダイヤグラムを描いたのち帰還ループの符号が全体で負になっているかを面倒でもいちいち確認したほうが良い。
3.結果
時間換算係数が \(a_{\tau}=1\) の場合の低速演算の結果を示す。
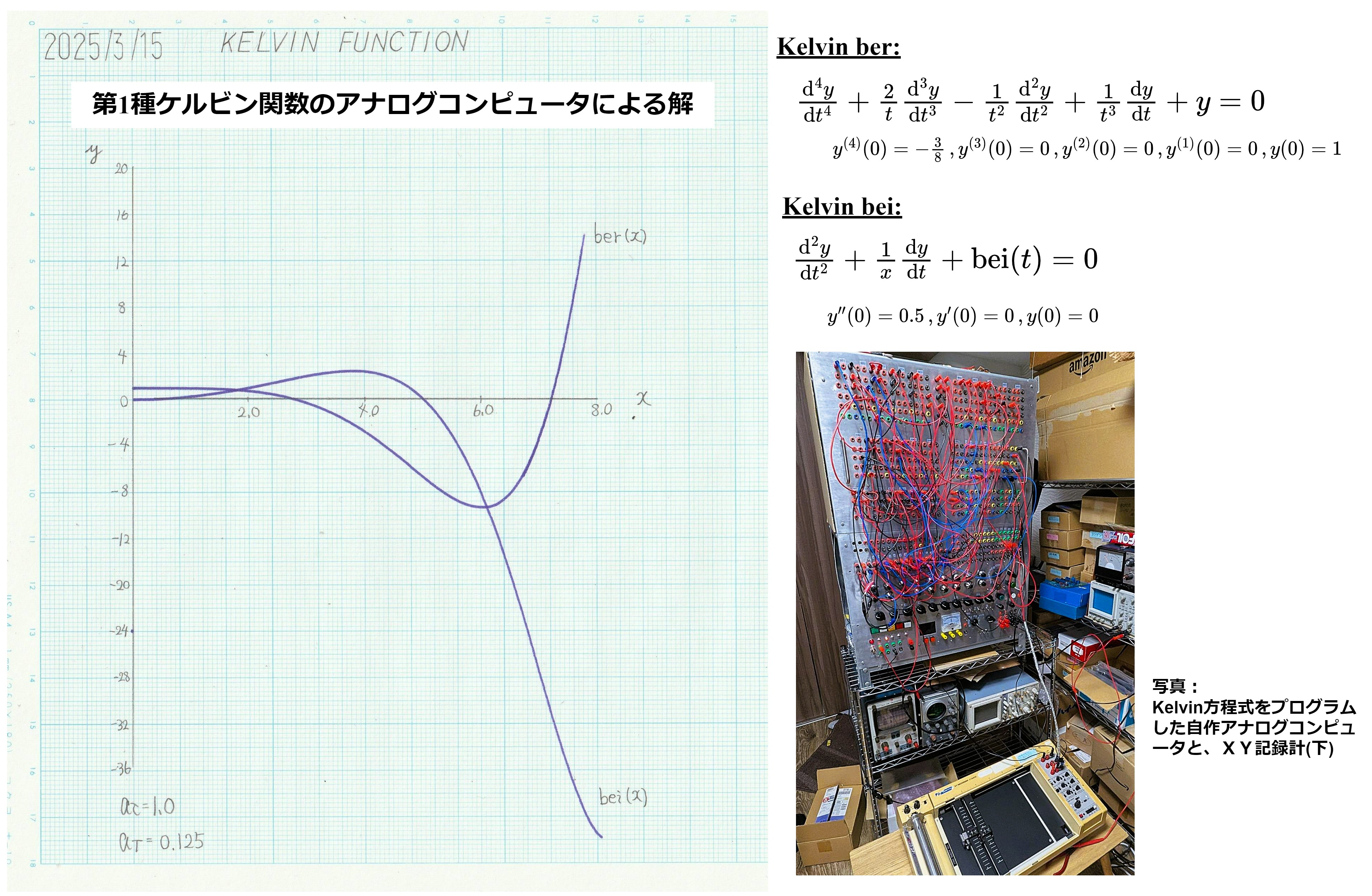
図3 アナログコンピュータによる第1種ケルビン関数の演算結果
4.参考文献
[1] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」第1版, 岩波書店, 1975.
[2] 平野 鉄太郎. 「ベッセル函数」第1版, 日新出版, 1963.