四重極電界内におけるイオン軌道
目次
1.準備
1.1 背景
四重極質量分析計は、図1に示すように互いに平行に配置された2組4本の円柱ロッド電極(四重極電極)が形成する電場で、特定の質量電荷比\(m/e\)[kg/C]を持つイオンを検出する質量分析計である。1953年にボン大学のWolfgang Paulがその原理を発見した。[1]
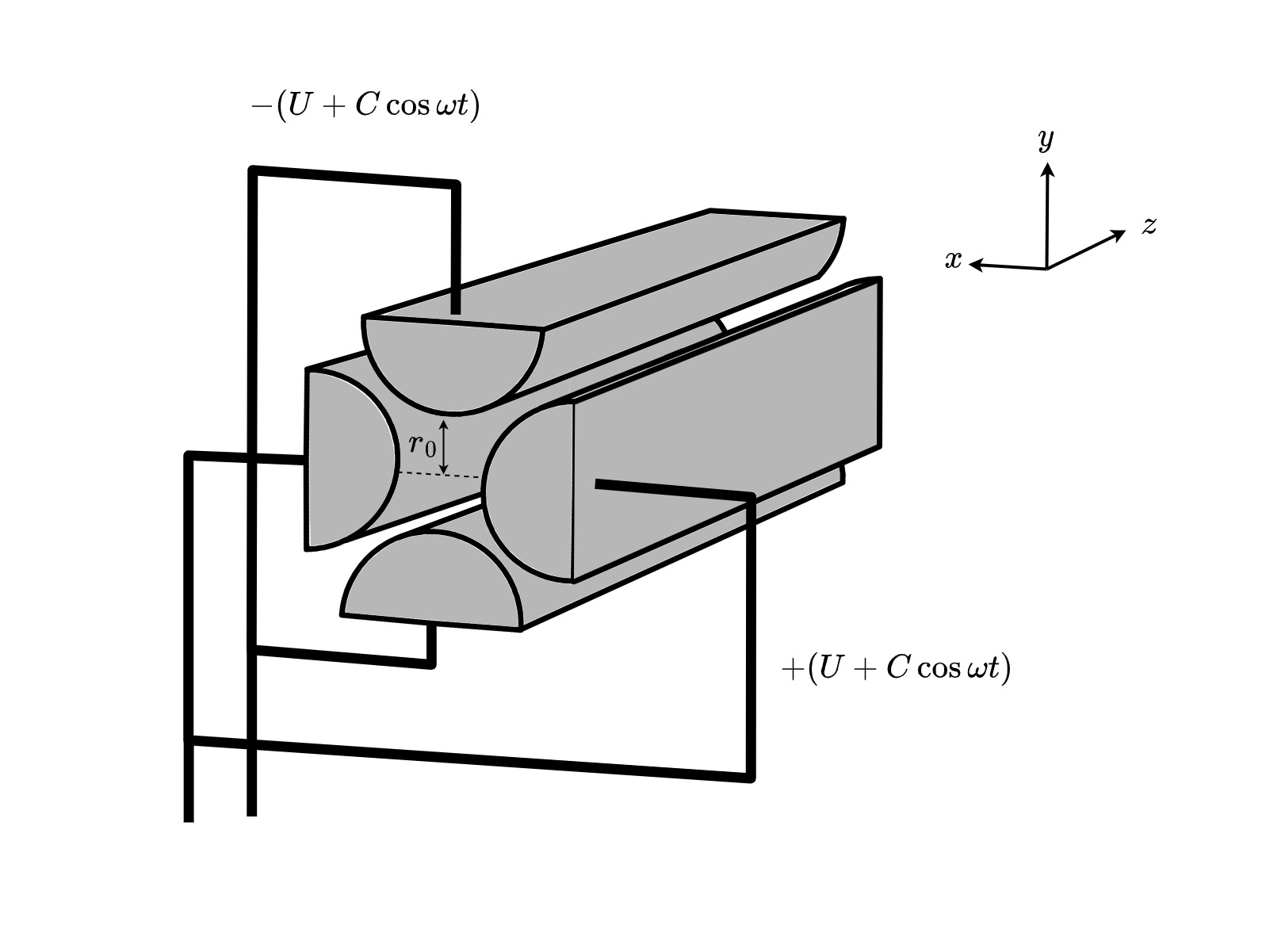
図に示すように\(x-y-z\)軸を設定し、四重極電極間距離を\(2r_0\)[m]とする。2対の電極のうち一方には\(+(U+V\cos{\omega{t}})\)[V]、もう一方には\(-(U+V\cos{\omega{t}})\)[V]と表される電圧(直流バイアスを掛けた交流電圧)を印加する。四重極電極内の電位\(\phi(x,y,z)\)[V]はポアソン方程式に従い、
\[\phi=\phi_0(\lambda x^2+\sigma y^2+\gamma z^2)\tag{1}\]
\[\nabla\phi=\left(\frac{\partial^2{\phi}}{\partial^2{x^2}}+\frac{\partial^2{\phi}}{\partial^2{y^2}}+\frac{\partial^2{\phi}}{\partial^2{z^2}}\right)=0\tag{2}\]
を満足する。(\(\lambda,\sigma,\gamma\)は定数)
以上の式から
\[\lambda+\sigma+\gamma=0\tag{3}\]
が導かれる。ここで、電極形状が、これらの定数が
\[\lambda=-\sigma=\frac{1}{r_0}\,,\gamma=0\tag{4}\]
なる関係を満たしている場合を考えよう。(1)式は
\[\phi=\frac{\phi_0}{{r_0}^2}(x^2-y^2)\tag{5}\]
となる。この場合の電極の断面は直角双曲線状になっている。\(z\)方向の電位は均一である。
\(x\)方向に\(+(U+V\cos{\omega t})\)、y方向に\(-(U+V\cos{\omega{t}})\)の電位差を掛けているので、四重極電極内電位は
\[\phi(x,y)=(U+V\cos{\omega{t}})\frac{x^2-y^2}{{r_0}^2}\tag{6}\]
となり、\(x\)軸方向、\(y\)軸方向、\(z\)軸方向の電場は各々
\begin{eqnarray}E_x&=&-\frac{\partial{\phi}}{\partial{x}}=-(U+V\cos{\omega{t}})\frac{2x}{{r_0}^2}\tag{7}\\\\E_y&=&-\frac{\partial{\phi}}{\partial{y}}=(U+V\cos{\omega{t}})\frac{2y}{{r_0}^2}\tag{8}\\\\E_z&=&-\frac{\partial{\phi}}{\partial{z}}=0\tag{9}\end{eqnarray}
と書ける。
次に、それぞれの方向のイオンの運動方程式を導く。イオンの質量を\(m\)[kg]、電荷を\(e\)[C]とすると
\begin{eqnarray}m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}&=&-2e(U+V\cos{\omega{t}})\frac{x}{{r_0}^2}\tag{10}\\\\m\frac{\mathrm{d}^2y}{\mathrm{d}t^2}&=&2e(U+V\cos{\omega{t}})\frac{y}{{r_0}^2}\tag{11}\\\\m\frac{\mathrm{d}^2z}{\mathrm{d}t^2}&=&0\tag{12}\end{eqnarray}
上式から、イオンは\(z\)軸方向には力を受けないので等速直線運動するが、\(x,y\)軸方向には周期的外力を受けることがわかる。
ここで以下の無次元変数を導入する。
\[\omega{t}=2\xi\;,\quad a=\frac{8eU}{m{r_0}^2\omega^2}\;,\quad q=\frac{4eV}{m{r_0}^2\omega^2}\tag{13}\]
\(a\) はイオンの受ける力の直流成分、\(q\) は外力の変調深さといえる。(10)、(11)式は以下のように書き直せる。
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}\xi^2}+(a+2q\cos{2\xi})x=0\tag{14}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}\xi^2}-(a+2q\cos{2\xi})y=0\tag{15}\end{eqnarray}
このように表される微分方程式をマシュー(Mathieu)の微分方程式という。また、マシューの微分方程式の解関数をマシュー関数と呼ぶ。マシューの微分方程式は、今回のようにラプラス方程式を放物面座標 (paraboloidal coordinate) で変数分離した際のほかに、ヘルムホルツ方程式を楕円柱座標 (Elliptic cylindrical coordinates) で変数分離する際に登場する。また、\(f(t)\) を周期関数として、
\[\frac{\mathrm{d}^2y}{\mathrm{dx^2}}+f(t)y=0\tag{16}\]
で表現されるヒル(Hill)の微分方程式の最も簡単な場合の1つである。
四重極電界内のイオンの軌跡は上式(14)、(15)に支配されているわけだが、\(x\)方向と\(y\)方向の変位が有界に留まり振動するか、それとも無限大に発散するかはパラメータ\(a\)と\(q\)の値によって決まる。
電極形状・印加電圧・周波数を特定の条件に固定すると、\(a\)と\(q\)の値はただイオンの質量電荷比にのみ依存する。言い換えれば、イオンの\(m/e\)値が\(a-q\,\)パラメータ平面の安定解領域に収まる場合は四重極電極内部を通過して検出部に到達でき、不安定解(発散解)領域に入っている場合は電極にトラップされて検出できない。
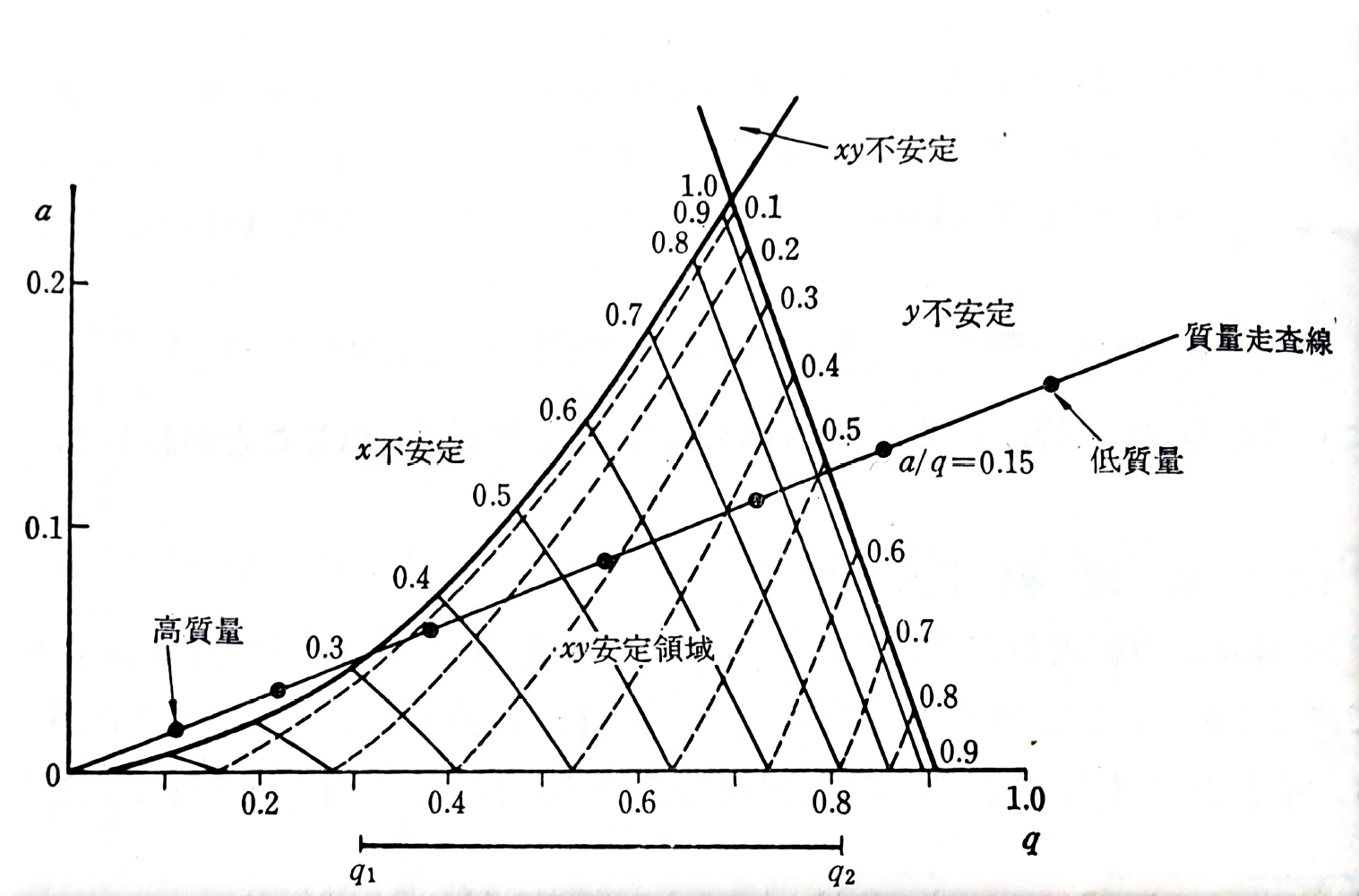
図2 安定線図 (文献[1] p.8の図1-4より引用 )
(13)式から
\[\frac{a}{2q}=\frac{U}{V}\tag{16}\]
であり、この比率は質量・電荷に無関係に決まるから、試料とする陽イオンの電荷が全て等しいとき、\(U/V\)比を一定にするとすべての異なった質量のイオンは\((a-q)\)平面上の傾き\(U/V\)の比例直線上に並ぶことになる。この直線を質量走査線という。この走査線の傾き\(U/V\)は、電極に印加する交流の直流バイアスの相対的大きさに他ならない。\(x\)方向の電圧\(+(U+V\cos{\omega{t}})\)が正極性となる時間が多く、一方\(y\)方向の電圧\(-(U+V\cos{\omega{t}})\)の電圧は負極性となる時間が多くなっている。前者は低質量陽イオン(僅かな時間の負電場にも容易に感応する)をトラップし、高質量陽イオン(うごきがのろく感応しにくい)は反発しトラップされない。後者は動きののろい高質量陽イオンを負電場により容易に捕捉するが、低質量陽イオンは周期の大部分を占める負極性電場であっても捕捉しにくく、通過させる。結果として、「丁度良い」質量のイオンのみが捕捉されず電極を通過できる。
質量走査線の傾き\(U/V\)を大きくしていくと、\(x\)電極や\(y\)電極ができるイオンの数が増えるので、通過できるイオンの質量数範囲は次第に狭くなり、限られたイオンしか検出部へ到達できなくなる。文献[1]によれば、
\[U/V=0.16784\tag{17}\]
のとき、質量走査線は原点近くの安定領域の頂点(\(a=0.23699\,,q=0.70600\))を通る。
2.アナログコンピュータプログラム
今回は、2組の微分方程式
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+\{a+2q\cos{(2t)}\}x&=&0\tag{14}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}t^2}-\{a+2q\cos{(2t})\}y&=&0\tag{15}\end{eqnarray}
を演算回路で構成し、陽イオンの四重極電極内における位置の時間変化をグラフィカルに求めることを目的とする。イオンは\(z\)方向については等速運動を行うから、\(z\)座標は独立変数\(t\)について適当に比例させればよい。一方、\(x\,,y\)座標は上記2式の解関数である。
また、方程式中の係数は\(0\leq{q}\leq{1}\;,0\leq{a}\leq{0.2}\)の範囲に限定する。
ゼロ除算の発生し得る極などの困難は特段見受けられないので、順当に陽関数法による実装を目指そう。最高階について解いた形は
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}&=&-ax-2q\cos{(2t)}x\tag{16}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}t^2}&=&ay+2q\cos{(2t})y\tag{17}\end{eqnarray}
となる。視察により、両式は全く同じ周期強制項 \(2q\cos{(2t)}\) を有していることがわかるから、この強制項を発生させる回路は(16),(17)で共通にでき、以下の3式を実現する3回路を構成すればよいことになる。
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}&=&-ax-f(t)x\tag{18}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}t^2}&=&ay+f(t)y\tag{19}\\\\f(t)&=&2q\cos{(2t)}\tag{20}\end{eqnarray}
手始めに、式(20)を生成しよう。当然、非減衰2階線形微分方程式を解いて、\(2q\)は初期条件とすればいいことが簡単に推察される。ただ、角周波数が1より大であるから、積分器出力の飽和に注意せねばならない。これまでの線形非斉次式では無視されてきた「電圧換算係数」に再登場願うことになる。まずは原方程式としていきなり2階微分方程式を考えるのではなく、2元の1階微分方程式に書き下してみる。
\begin{eqnarray}f(t)&=&2q\cos{(2t)}&&\qquad(|f(t)|_{\mathrm{max}}=2)\tag{21}\\\\g(t)&\equiv&{f'(t)}=-4q\sin{(2t)}&&\qquad(|g(t)|_{\mathrm{max}}=4)\tag{22}\\\\g'(t)&=&-8q\cos{(2t)}=-4f(t)&&\qquad(|g'(t)|_{\mathrm{max}}=8)\tag{23}\end{eqnarray}
であるから、原方程式は
\[\left\{\begin{array}{ll}\displaystyle{\frac{\mathrm{d}g}{\mathrm{d}t}}&=&-4f\\\\\displaystyle{\frac{\mathrm{d}f}{\mathrm{d}t}}&=&g\end{array}\right.\tag{24}\]
演算方程式に直すと
\[\left\{\begin{array}{ll}\displaystyle{\frac{a_{\tau}}{a_{G}}\frac{\mathrm{d}G}{\mathrm{d}\tau}}&=&\displaystyle{-4\frac{F}{a_{F}}}\\\\\displaystyle{\frac{a_{\tau}}{a_{F}}\frac{\mathrm{d}F}{\mathrm{d}\tau}}&=&\displaystyle{\frac{G}{a_{G}}}\end{array}\right.\tag{24}\]
各変数の最大値を鑑みて、\(a_{F}=\frac{1}{2}\;,a_{G}=\frac{1}{4}\)と設定すると、
\[\left\{\begin{array}{ll}\displaystyle{a_{\tau}\frac{\mathrm{d}G}{\mathrm{d}\tau}}&=&\displaystyle{-2\frac{F}{a_{F}}}\\\\\displaystyle{a_{\tau}\frac{\mathrm{d}F}{\mathrm{d}\tau}}&=&\displaystyle{2\frac{G}{a_{G}}}\end{array}\right.\tag{25}\]
となる。時間換算係数は好きにしてよいが、通例通り、低速モードの時は\(a_{\tau}=1\)、高速モードでは\(a_{\tau}=10^{-3}\)にするのがよい。コンデンサの切り替えスイッチによって即座に時間換算係数を変化できる。
つぎに(18)式に対処する。線形微分方程式であるが、変化係数を有するから乗算器が必要である。最大値の推算は困難であるが、安定領域内では初期条件を十分小さくすれば1以内に収まると想像できるので、まずは\(a_{X}=a_{\dot{X}}=1\)としてよい。最高階である2階微分項についても、電圧信号として現れないので \(a_{X}\) と共通させて良い。演算方程式
\[\frac{{a_{\tau}}^2}{a_{X}}\frac{\mathrm{d}^2X}{\mathrm{d}\tau^2}=-a\frac{X}{a_{X}}-\frac{F}{a_{F}}\frac{X}{a_{X}}\tag{26}\]
に \(a_{F}=1/2\,,a_{X}=1\) を代入すると、
\[{a_{\tau}}^2\frac{\mathrm{d}^2X}{\mathrm{d}\tau^2}=-aX-2FX\tag{27}\]
\(a\)の値は1以下としているので、(27)式は演算回路として構成可能である。
(19)式についても同様の処置を行う。ただ符号が変わるだけである。
\[{a_{\tau}}^2\frac{\mathrm{d}^2Y}{\mathrm{d}\tau^2}=aY+2FY\tag{28}\]
(25),(27),(28)に基づくブロックダイヤグラムを以下に示す。
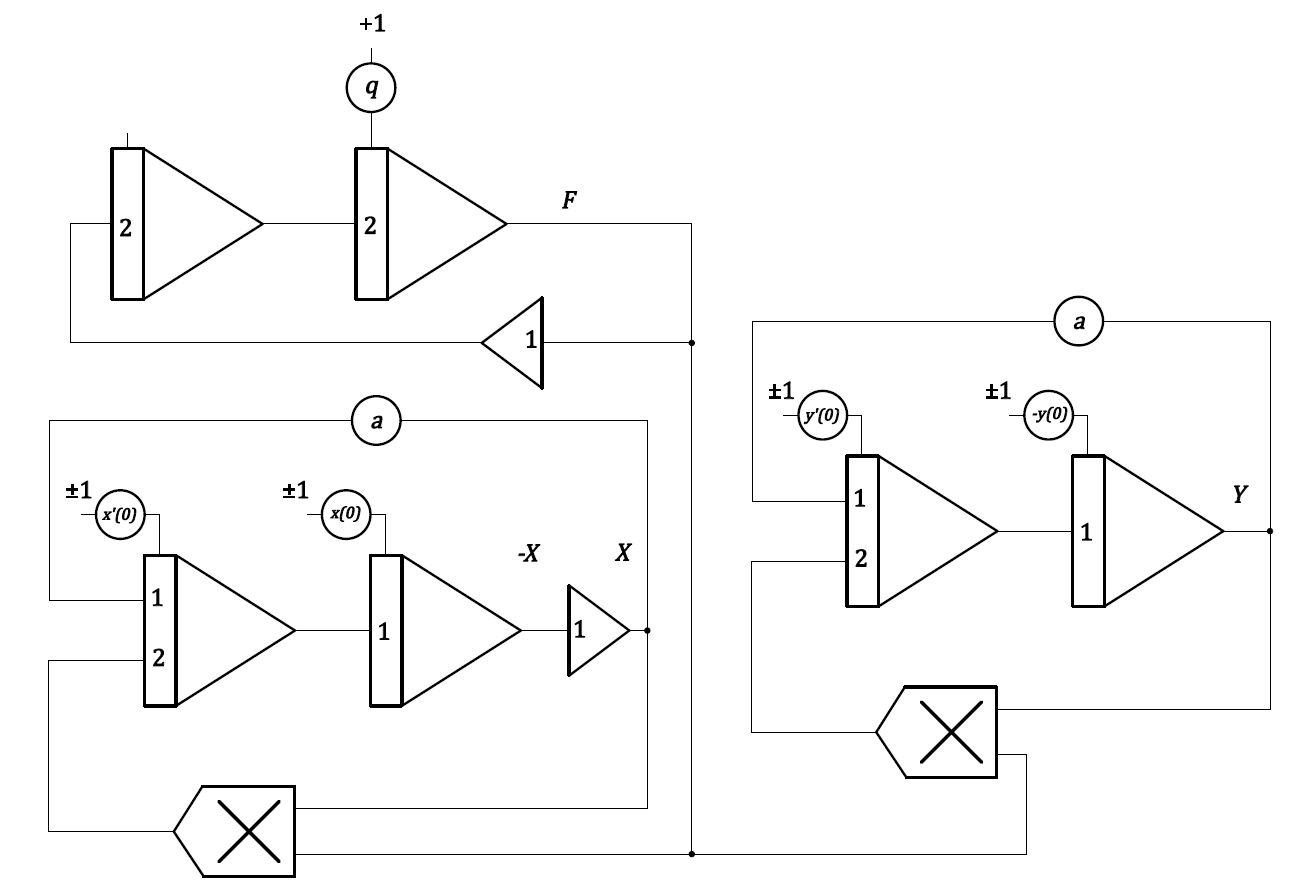
図3 ブロックダイヤグラム
初期条件\(2q\)は\(a_{F}=1/2\)の効果により\(q\)にスケーリングされていることに注意。
3.結果
\(x,y\)時系列グラフを低速モードでアナログオシロに表示させた結果を示す。初期条件は、1階微分項のみ \(-0.1\) を与えている。パラメータはグラフ用紙中に記入された値であり、いずれも安定領域内である。
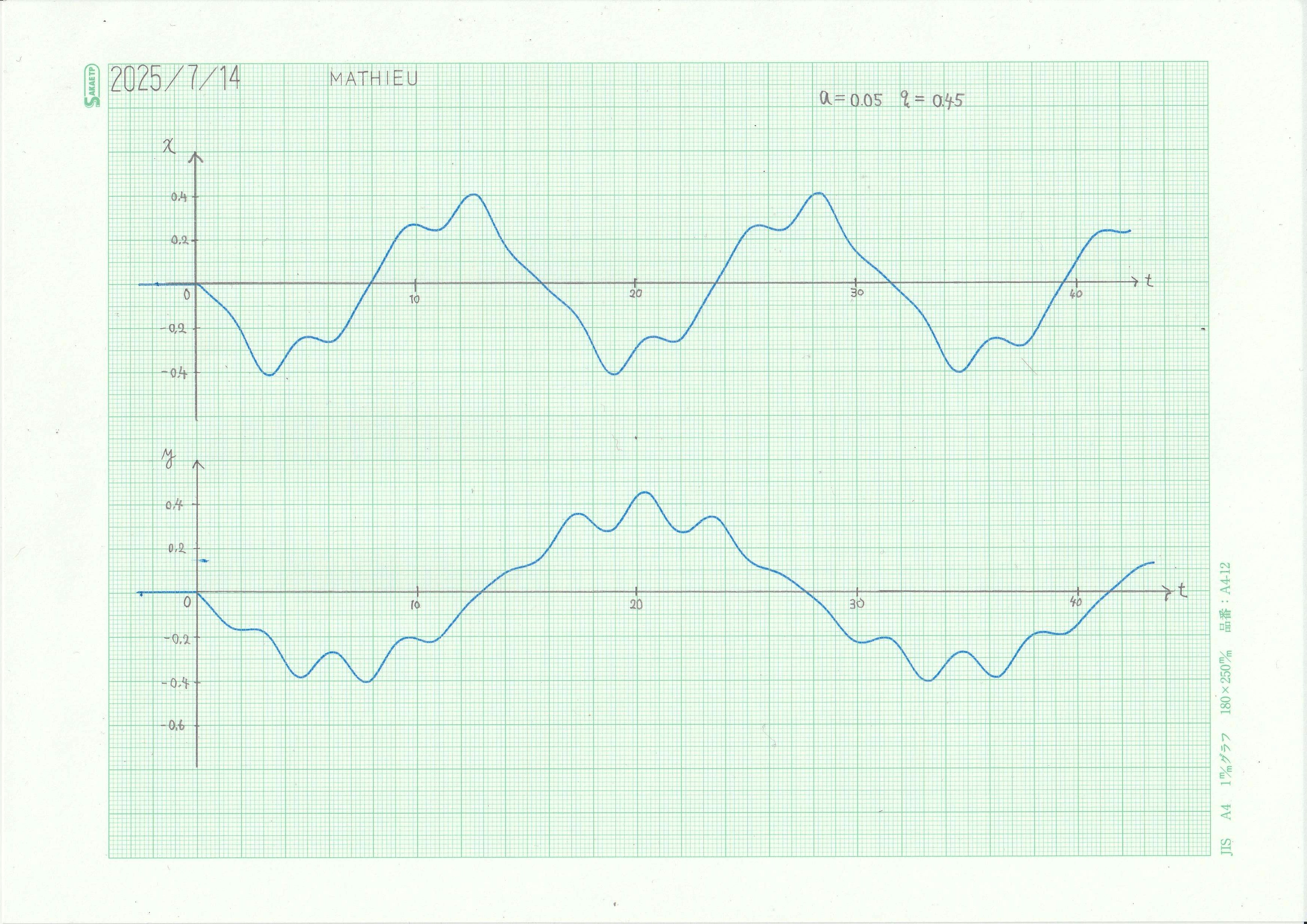
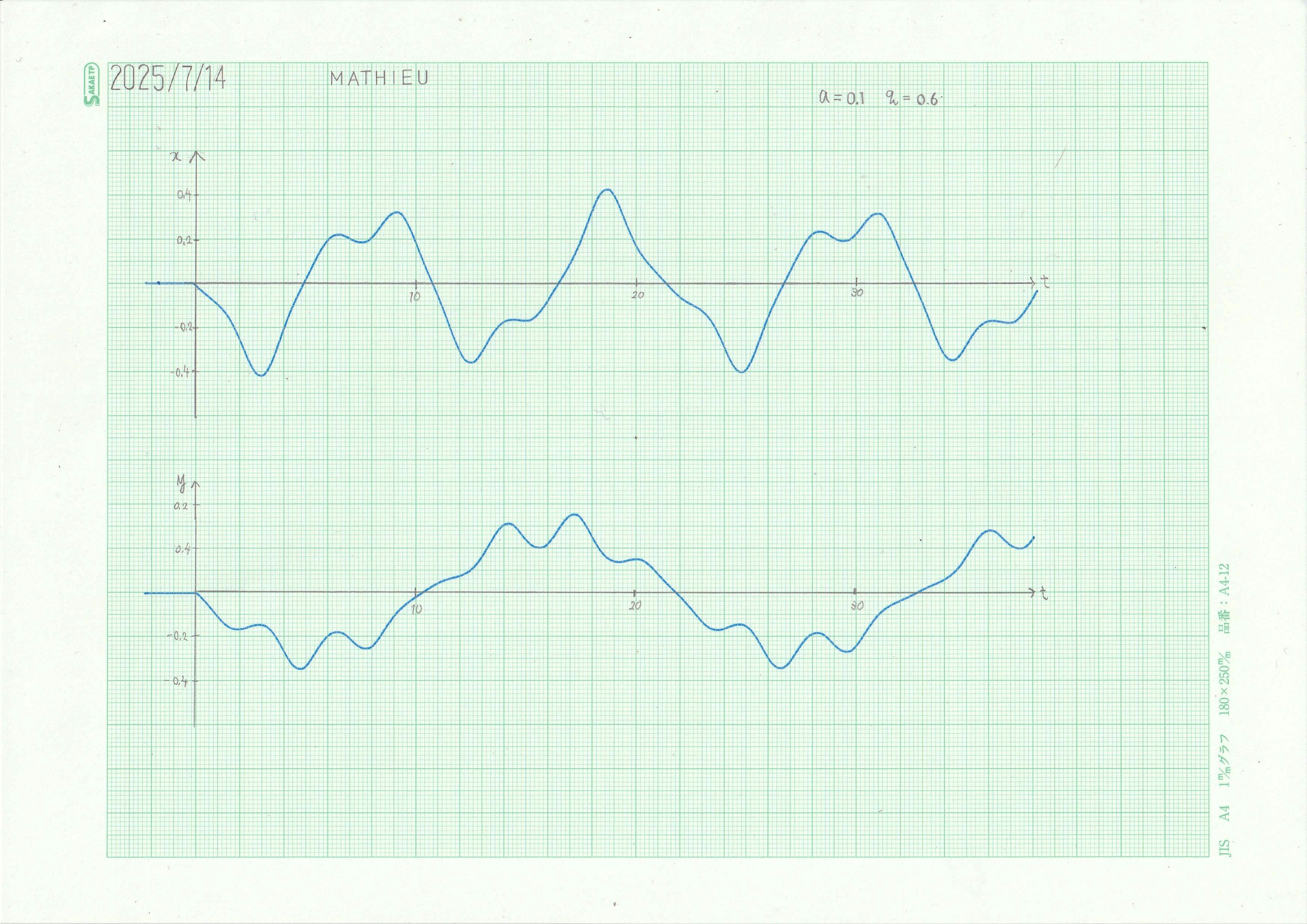
図4 アナログコンピュータによる演算結果
\(x\), \(y\) ともに概周期軌道となっている。
\(a=0.05\,,q=0.45\) の場合の、進行方向(z軸)から見た軌道の様子は以下のようになる。
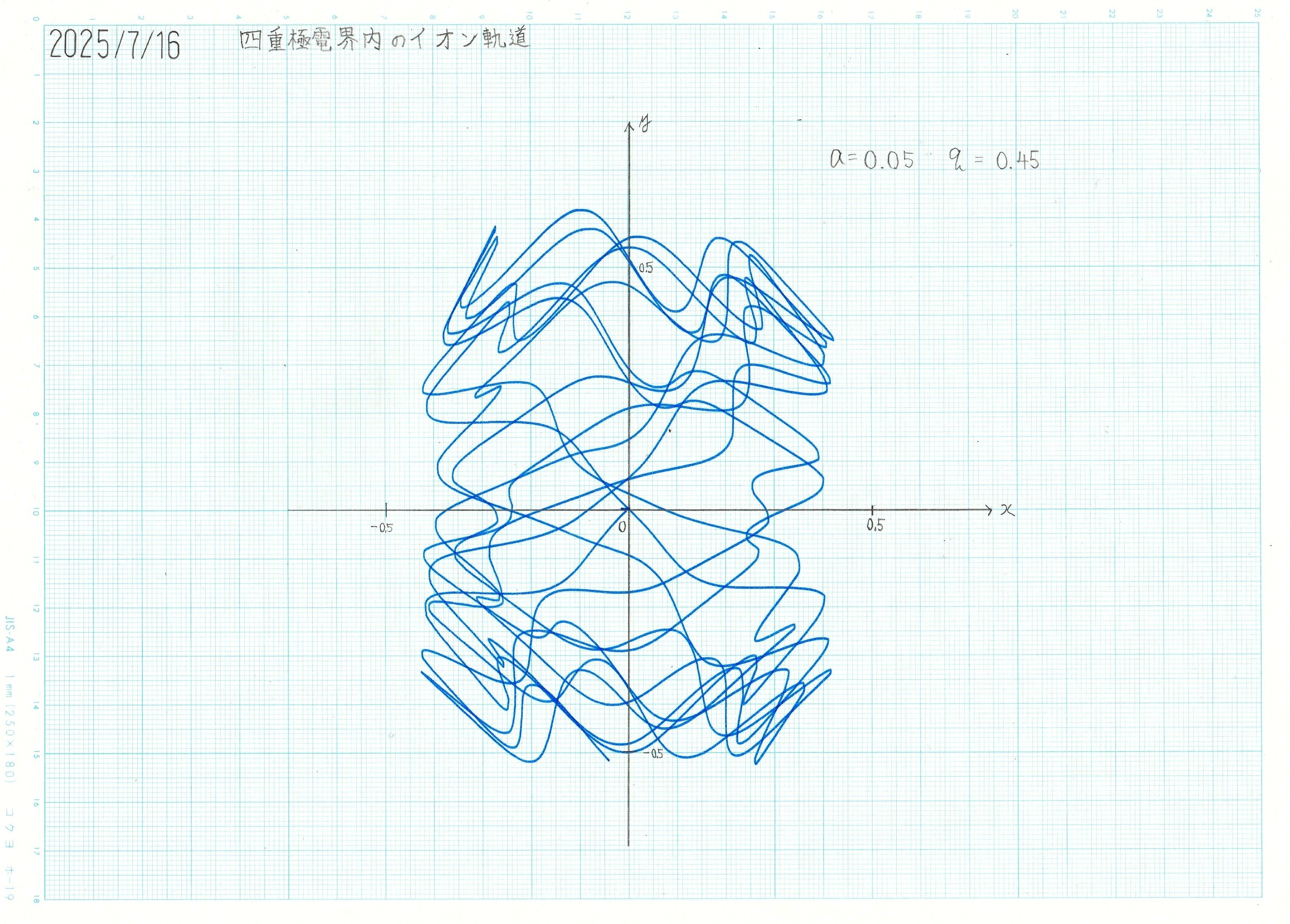
図5 z軸上から見たイオン軌道
また、高速モードに設定し、出力信号に回転行列を掛ける回路を設けると、イオン軌道の俯瞰図を得ることもできる。詳しくは、便利なブロックダイヤグラムのページを参照。
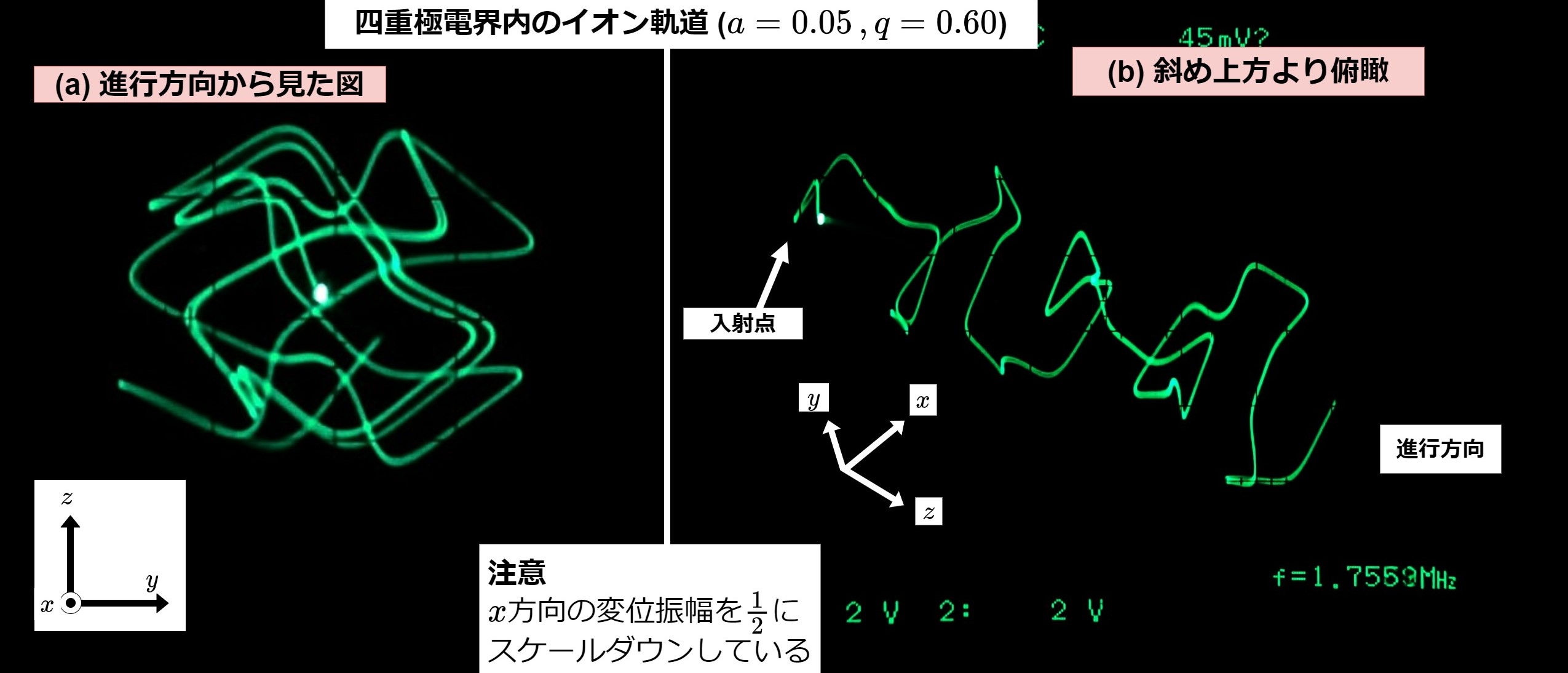
図6 正面図と俯瞰図

図7 マシュー方程式と回転行列のプログラムを施したあとの自作アナログコンピュータの写真
ついでに、Pythonでマシュー方程式を計算し、イオン軌道を俯瞰する動画を作ってみた。manimというアニメーションエンジンを使っている。デジタル計算機の便利さを改めて実感した。
4.参考文献
[1] 不破敬一郎, 藤井敏博.「四重極質量分析計:原理と応用」第1版, 講談社, 1977.
[2] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」第1版, 岩波書店, 1975.
[3] Toshio Kondo."Analog Computation of Ion Trajectories in a Mass Filter," Journal of the Mass Spectrometry Society of Japan, 1969, 17 巻, 2 号, p. 589-602.
[4] EAI. "Solution of Mathieu’s Equation on the Analog Computer, Applications Reference Library," Application Study: 7.4.4a, 1964.