2重振り子のシミュレーション
目次
1.オイラー・ラグランジュ方程式
図1.1のような平面上を運動する2重振り子系の演算回路を、オイラー・ラグランジュの方程式をもとに構成し、アナログコンピュータによるシミュレーションを行う。
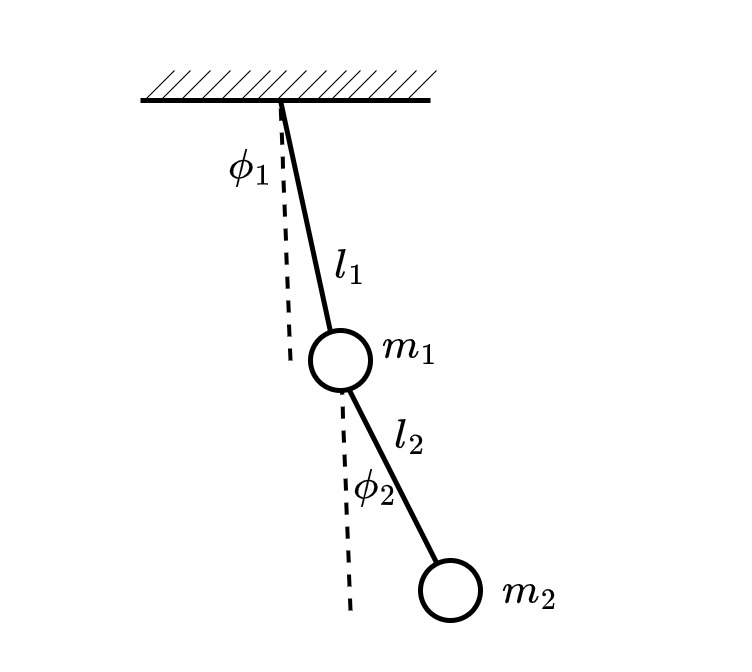
図 1 2重振り子
2質点には重力と張力のみが働き、空気抵抗等は無視するものとする。腕1が天井に固定されている点を原点\(O\)として、鉛直下向きにy軸、水平方向向かって右向きにx軸を設定し、質量が無視できる細い腕1(長さ\(l_1\))、腕2(長さ\(l_2\))が鉛直方向と為す角をそれぞれ\(\phi_1,\phi_2\)とする。また、質点1と質点2の質量はそれぞれ\(m_1,m_2\)、質点1,2の座標をそれぞれ\((x_1,y_1),(x_2,y_2)\)と設定する。
角度\(\phi\)を一般化座標としてそれぞれの質点速度\(v_1,v_2\)の2乗を計算すると、
\begin{eqnarray}x_1&=&l_1\sin{\phi_1}\\y_1&=&l_1\cos{\phi_1}\\{v_1}^2&=&\dot{x_1}^2+\dot{y_1}^2\\&=&(l_1\dot{\phi}_1\cos{\phi_1})^2+(-l_1\dot{\phi1}\sin{\phi_1})^2\\&=&{l_1}^2\dot{\phi}_1^2\tag{1}\\\\x_2&=&l_1\sin{\phi_1}+l_2\sin{\phi_2}\\y_2&=&l_1\cos{\phi_1}+l_2\cos{\phi_2}\\{v_2}^2&=&\dot{x_2}^2+\dot{y_2}^2\\&=&(l_1\dot{\phi}_1\cos{\phi_1}+l_2\dot{\phi}_2\cos{\phi_2})^2+(-l_1\dot{\phi}_1\sin{\phi_1}-l_2\dot{\phi}_2\sin{\phi_2})^2\\&=&{l_1}^2{\dot{\phi}_1}^2+l_2^2\dot{\phi}_2^2+2l_1l_2\dot{\phi}_1\dot{\phi}_2\cos{(\phi_1-\phi_2)}\tag{2}\end{eqnarray}
各質点の運動エネルギー\(T_1,T_2\)及びポテンシャル\(U_1,U_2\)は
\begin{eqnarray}T_1&=&\frac{1}{2}m_1v_1^2\\&=&\frac{1}{2}m_1{l_1}^2{\dot{\phi}_1}^2\tag{3}\\\\U_1&=&m_1\,g\,y_1\\&=&m_1\,g\,l_1\cos{\phi_1}\tag{4}\\\\T_2&=&\frac{1}{2}m_2v_2^2\\&=&\frac{1}{2}m_2\left\{{l_1}^2{\dot{\phi}_1}^2+{l_2}^2{\dot{\phi}_2}^2+2l_1l_2\dot{\phi}_1\dot{\phi}_2\cos{(\phi_1-\phi_2)}\right\}\tag{5}\\\\U_2&=&m_2\,g\,y_2\\&=&m_2\,g\,(l_1\cos{\phi_1}+l_2\cos{\phi_2})\tag{6}\end{eqnarray}
以上より、2重振り子系のラグランジュ関数\(L\)は
\begin{eqnarray}L&=&T-U\\&=&(T_1+T_2)-(U_1+U_2)\\&=&\frac{1}{2}m_1{l_1}^2{\dot{\phi}_1}^2+\frac{1}{2}m_2\left\{{l_1}^2{\dot{\phi}_1}^2+{l_2}^2{\dot{\phi}_2}^2+2l_1l_2\dot{\phi}_1\dot{\phi}_2\cos{(\phi_1-\phi_2)}\right\}-m_1\,g\,l_1\cos{\phi_1}-m_2\,g(l_1\cos{\phi_1}+l_2\cos{\phi_2})\\&=&\frac{1}{2}(m_1+m_2){l_1}^2{\dot{\phi}_1}^2+\frac{1}{2}m_2{l_2}^2{\dot{\phi}_2}^2+m_2l_1l_2\dot{\phi}_1\dot{\phi}_2\cos{(\phi_1-\phi_2)}+(m_1+m_2)\,g\, l_1\cos{\phi_1}+m_2\,g\,l_2\cos{\phi_2}\tag{7}\end{eqnarray}
これをラグランジュの運動方程式
\begin{eqnarray}\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial{L}}{\partial{\dot{\phi}_1}}-\frac{\partial{L}}{\partial{\phi_1}}=0\tag{8}\\\\\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial{L}}{\partial{\dot{\phi}_2}}-\frac{\partial{L}}{\partial{\phi_2}}=0\tag{9}\end{eqnarray}
に代入して具体的に計算する。要求されている微分項を求めると、
\begin{eqnarray}-\frac{\partial{L}}{\partial{\phi_1}}&=&m_2l_1l_2\dot{\phi}_1\dot{\phi}_2\sin(\phi_1-\phi_2)+(m_1+m_2)\,g\,l_1\sin{\phi_1}\tag{10}\\\\\frac{\partial{L}}{\partial{\dot{\phi}_1}}&=&(m_1+m_2){l_1}^2{\dot{\phi}_1}+m_2l_1l_2\dot{\phi}_2\cos{(\phi_1-\phi_2)}\tag{11}\\\\\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial{L}}{\partial{\dot{\phi}_1}}&=&(m_1+m_2){l_1}^2\ddot{\phi}_1+m_2l_1l_2\left\{\ddot{\phi}_2\cos{(\phi_1-\phi_2)}-\dot{\phi}_2(\dot{\phi}_1-\dot{\phi}_2)\sin{(\phi_1-\phi_2)}\right\}\tag{12}\\\\-\frac{\partial{L}}{\partial{\phi_2}}&=&-m_2l_1l_2\dot{\phi}_1\dot{\phi}_2\sin{(\phi_1-\phi_2)}+m_2\,g\,l_2\sin{\phi_2}\tag{13}\\\\\frac{\partial{L}}{\partial{\dot{\phi}_2}}&=&m_2{l_2}^2\dot{\phi}_2+m_2l_1l_2\dot{\phi}_1\cos{(\phi_1-\phi_2)}\tag{14}\\\\\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial{L}}{\partial{\dot{\phi}_2}}&=&m_2{l_2}^2\ddot{\phi}_2+m_2l_1l_2\biggl\{\ddot{\phi}_1\cos{(\phi_1-\phi_2)}-\dot{\phi}_1(\dot{\phi}_1-\dot{\phi}_2)\sin{(\phi_1-\phi_2)}\biggr\}\tag{15}\\\\\end{eqnarray}
これらを(8)式に代入して、最高微分階数項\(\ddot{\phi}_1\)について解いた形に変形する。
\begin{eqnarray}(m_1+m_2){l_1}^2\ddot{\phi}_1+m_2l_1l_2\left\{\ddot{\phi}_2\cos{(\phi_1-\phi_2)}-\dot{\phi}_2(\dot{\phi}_1-\dot{\phi}_2)\sin{(\phi_1-\phi_2)}\right\}+m_2l_1l_2\dot{\phi}_1\dot{\phi}_2\sin(\phi_1-\phi_2)+(m_1+m_2)\,g\,l_1\sin{\phi_1}&=&0\\\\(m_1+m_2){l_1}^2\ddot{\phi}_1+m_2l_1l_2\ddot{\phi}_2\cos{(\phi_1-\phi_2)}+m_2l_1l_2{\dot{\phi}_2}^2\sin{(\phi_1-\phi_2)}+(m_1+m_2)\,g\,l_1\sin{\phi_1}&=&0\\\\{l_1}^2\ddot{\phi}_1+\frac{m_2}{m_1+m_2}l_1l_2\ddot{\phi}_2\cos{(\phi_1-\phi_2)}+\frac{m_2}{m_1+m_2}l_1l_2{\dot{\phi}_2}^2\sin{(\phi_1-\phi_2)}+g\,l_1\sin{\phi_1}&=&0\\\\\ddot{\phi}_1+\frac{m_2}{m_1+m_2}\frac{l_2}{l_1}\ddot{\phi}_2\cos{(\phi_1-\phi_2)}+\frac{m_2}{m_1+m_2}\frac{l_2}{l_1}{\dot{\phi}_2}^2\sin{(\phi_1-\phi_2)}+\frac{g}{l_1}\sin{\phi_1}&=&0\end{eqnarray}
従って
\[\ddot{\phi}_1=-\frac{m_2}{m_1+m_2}\frac{l_2}{l_1}\left\{\ddot{\phi}_2\cos{(\phi_1-\phi_2)}+{\dot{\phi}_2}^2\sin{(\phi_1-\phi_2)}\right\}-\frac{g}{l_1}\sin{\phi_1}\tag{16}\]
(9)式についても同様に変形すると
\[\ddot{\phi}_2=-\frac{l_1}{l_2}\left\{\ddot{\phi}_1\cos{(\phi_1-\phi_2)}-\dot{\phi}_1\sin{(\phi_1-\phi_2)}\right\}-\frac{g}{l_2}\sin{\phi_2}\tag{17}\]
導かれた(16)式と(17)式が今回の原方程式である。
2.アナログコンピュータプログラム
2.1 演算方程式
今回は簡単のため、\(m_1=m_2=1\:\rm{kg}\),\(\quad l_1=l_2=1\:\rm{m}\)に固定する。原方程式は、角度についての連立2階非線形常微分方程式
\begin{eqnarray}\ddot{\phi}_1&=&-\frac{1}{2}\left\{\ddot{\phi}_2\cos{(\phi_1-\phi_2)+{\dot{\phi_{2}}}^2\sin{(\phi_1-\phi_2)}+2g\sin{\phi_1}}\right\}\tag{18}\\\\\ddot{\phi}_2&=&-\left\{\ddot{\phi}_1\cos{(\phi_1-\phi_2)}-\dot{\phi}_1^2\sin{(\phi_1-\phi2)}+g\sin{\phi_2}\right\}\tag{19}\end{eqnarray}
となる。陽関数法でstraightforwardに演算できるが、通常とは異なり、最高階項 \(\ddot{\phi_{1}}\,,\ddot{\phi_{2}}\) が演算に必要であるから、2階微分項を電圧信号として確保できるよう、縦続積分器群の上流に加算器が必要になることに注意。
原変数のうち、正弦・余弦などは当然その絶対値が1を超えないので、スケーリングは省略できる。しかし、角速度・角加速度の項はそのままだと信号が飽和してしまうので、適宜時間延引する必要がある。
今回は各変数をただ時系列・相平面グラフとして表示するだけではなく、XYモードのオシロスコープ画面に振り子の腕の動きを視覚的に表示することを目指す。その際必要となる振り子の表示回路は文献[2]を参考にした。
2.2 ブロックダイヤグラム
(18),(19)を実現するブロックダイヤグラムを以下に示す。
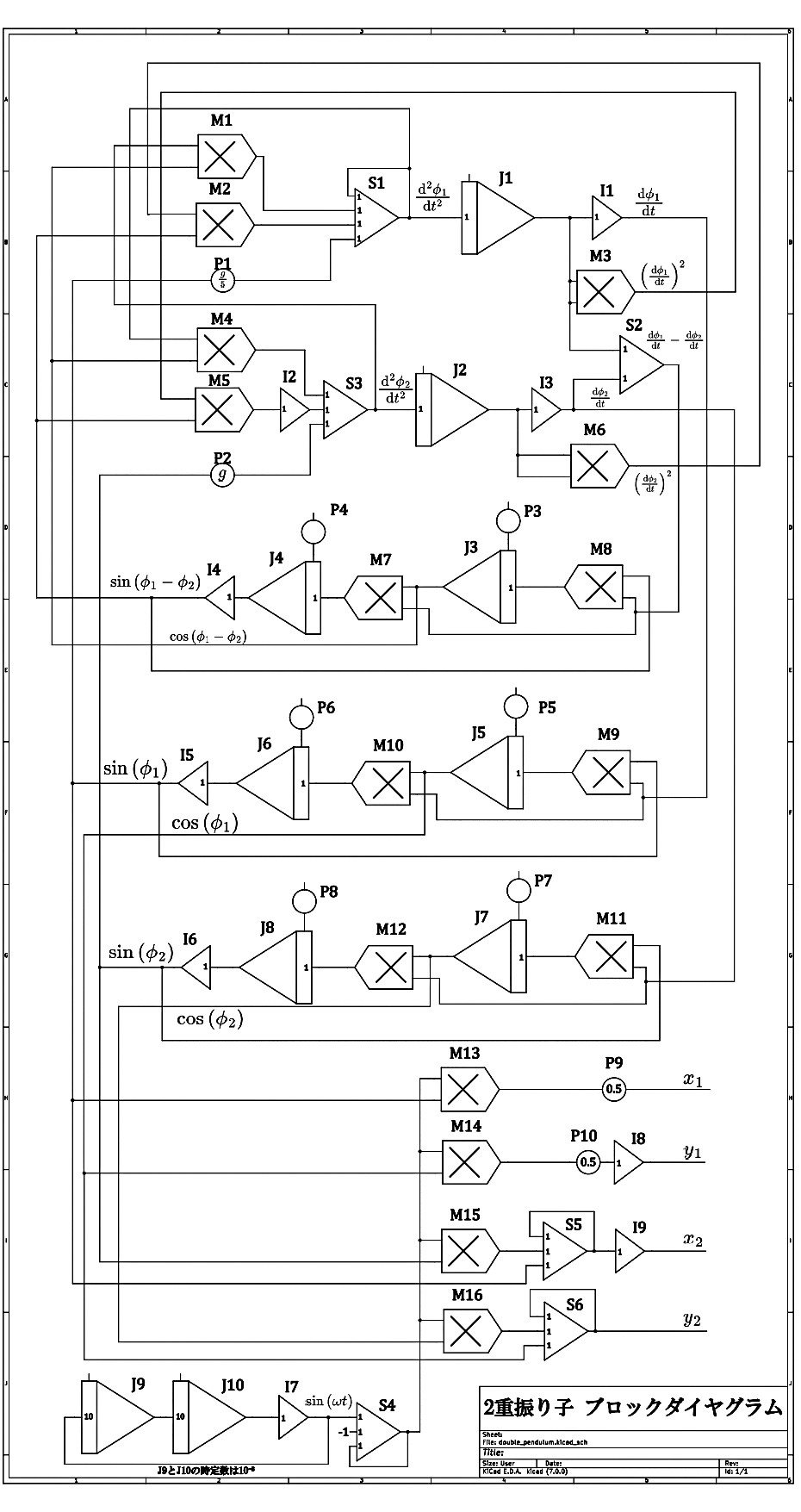
図2 2重振り子のブロックダイヤグラム
乗算器は16個、積分器は10個、加算器6個と、主要演算器は軒並み総動員である。(意外にも、演算器の不足より、バナナプラグパッチコードの不足のほうが深刻であった。)
角度\(\phi_{1}(t)\,,\phi_{2}(t)\,,(\phi_1(t)-\phi_2(t))\)の正弦・余弦関数が必要であるが、微分値\(\dot{\phi_{1}}\,,\dot{\phi_{2}}\,,{(\dot{\phi_1}-\dot{\phi_2})}\)が演算回路中で利用可能であるから、関数発生器に頼らず、微分方程式を利用する生成法を採用した。
生成する4変数(\(x_1,y_1,x_2,y_2\))はそれぞれ腕1、腕2の位置を表す信号であり、同時に表示させるためには2wayのマルチプレクサ2つが必要になる。ブロックダイヤグラムにあるとおり、アナログコンピュータにあらかじめ用意されている比較器と関数発生器(高周波方形波を得るため)でマルチプレクサを模擬できる。
腕の描画に必要な高周波正弦波については、図2においては微分方程式を解くことで発生させているが、外部のファンクションジェネレータ等の正弦波を利用できる場合は、そちらで代用してもよい。
積分器の時定数や入力端子のゲインに注意する事。角速度、角加速度をオシロで監視し、飽和すればその都度スケーリングを見直すことをお勧めする。
重力加速度を標準値 9.806... m/s にしたいなら、加算器S1、S3の入力ゲインを調整して係数器の値は\(g/10\)を設定したうえで、J1、J2の時間換算係数を大きくする必要があるだろう。あまり時間換算係数を大きくし過ぎると、今度は動きが緩慢になってリアルに感じられなくなる。それよりは、時間換算係数を大きくせず、重力加速度を小さく設定したほうがよい。
ちなみに、減衰のある2重振り子をシミュレーションしたい場合は、各角度の時間微分に比例した抵抗力を想定し、図2中の積分器 \(J_1\,,J_2\) の入出力端子間に適当な値に設定した係数器を介して負のフィードバックを掛ける。(積分器自体が符号変換を行っているため、フィードバックに反転器などは必要ない。)
3.結果
非減衰2重振り子と、減衰2重振り子のシミュレーションを行った。リアルタイムシミュレーションは動画でないと分からないと思うので、YouTubeにあげたもののリンクをここに貼っておく。角度の初期条件は\(\phi_1(0)=\pi\,,\phi_2(0)=0\) で、角速度・角加速度の初期値は全て0とした。
アナログコンピュータでここまで複雑なシミュレーションを実行でき、かつ直感的な表示も得られることに、ただただ驚嘆するのみである。ただし、3重振り子以上の質点系だと積分器や乗算器がさらに必要になる。演算器の個数による計算容量の制限は並列計算機の大きな欠点の1つであるが、直並列化(ハイブリッドコンピューティング)で幾分か緩和されるだろう。
4.参考文献
[1] https://www.aihara.co.jp/~taiji/pendula-equations/present-node2.html
[2] ANALOG PARADIGM, "Analog Computer Applications , Simulating a double pendulum" https://analogparadigm.com/downloads/alpaca_21.pdf