フレネル回折のシミュレーション
目次
アナログコンピュータでキルヒホフの積分表示を直接演算し、無限長スリットによるフレネル領域での回折光強度のグラフ化を試みる。

オーギュスタン・ジャン・フレネル Augustin Jean Fresnel (1788-1827)
Fondo Antiguo de la Biblioteca de la Universidad de Sevilla from Sevilla, España - "Agustin Fresnel"., CC 表示 2.0, リンクによる
1. キルヒホフの回折理論
1.1 ヘルムホルツ方程式の導出
キルヒホフの回折理論の基礎であるヘルムホルツ・キルヒホフの積分表示は、電磁気学の基礎方程式であるマクスウェル方程式と、ベクトル解析の公式(3次元のグリーンの定理)から導出できる。
まずはヘルムホルツ方程式を導出する。
電荷が無く無損失の媒質(自由空間)でのマクスウェル方程式の1つ、ファラデー・マクスウェルの式
\[\nabla \times \boldsymbol{E} = - \frac{ \partial{ \boldsymbol{B} } }{\partial t} \tag{1}\]
から出発する。\(\boldsymbol{E}\)と\(\boldsymbol{H}\)のみでフェーザ表示にすると
\[\nabla \times \boldsymbol{E} = - j\omega\mu\boldsymbol{H} \tag{2}\]
(2)の両辺のrot(回転)をとり
\begin{eqnarray} \nabla \times \nabla \times \boldsymbol{E} &=& - j\omega\mu(\nabla \times \boldsymbol{H}) \\ \nabla ( \nabla \cdot \boldsymbol{E} )-\nabla^2 \boldsymbol{E} &=& -j\omega\mu (\nabla \times \boldsymbol{H}) \tag{3} \end{eqnarray}
電場の湧き出しが存在しないので
\[\nabla^2 \boldsymbol{E} = j\omega\mu(\nabla \times \boldsymbol{H}) \tag{4}\]
これにマクスウェル・アンペールの式
\[\nabla\times \boldsymbol{H} = j\omega\varepsilon\boldsymbol{E} \tag{5}\]
を代入すれば
\[\nabla^2 \boldsymbol{E} = -\omega^2 \mu\varepsilon \boldsymbol{E} \tag{6}\]
波数 \(k=\omega \sqrt{\mu \varepsilon}\) を用いて
\[\nabla^2 \boldsymbol{E} = -k^2 \boldsymbol{E} \tag{7}\]
(7)式がヘルムホルツ方程式である。電界\(\boldsymbol{E}\)を複素振幅のみ考えたスカラ関数 \(u(\boldsymbol{r})\)とし、(球面波を考えるので)球面座標系に書き直すと
\[ \frac{1}{r} \frac{\partial{}}{\partial{t}} \left( r^2 \frac{ \partial{u} }{ \partial{t} } \right) + k^2 \boldsymbol{E} \tag{8}\]
(8)の素解は
\[ u = A \frac{\exp{(-jkr)}}{r} \tag{9}\]
(9)が球面波の式である。
1.2 ヘルムホルツ・キルヒホフの積分表示の導出
単純閉曲面\(S\)に囲まれた閉空間\(V\)において定義されるスカラ関数 \(\psi, \phi\)について、
\[ \nabla(\psi \nabla \phi - \phi \nabla \psi) =\phi \nabla^2 \psi - \phi \nabla^2 \psi \tag{10}\]
これを閉空間Vで体積積分する。(閉空間Vで導関数・2次導関数ともに連続であるとする)
\[ \int_V{\nabla(\psi \nabla \phi - \phi \nabla \psi)}\mathrm{d}V =\int_V{\phi \nabla^2 \psi - \phi \nabla^2 \psi}\mathrm{d}V \tag{11}\]
ガウスの定理を用いて左辺を面積積分に変えれば
\[ \int_S{(\psi \nabla \phi - \phi \nabla \psi)}\mathrm{d}\boldsymbol{S} =\int_V{\phi \nabla^2 \psi - \phi \nabla^2 \psi}\mathrm{d}V \tag{12}\]
ここで、関数\(\psi,\phi\)がヘルムホルツ方程式を満たす(\(\nabla^2\psi+k\psi=0, \nabla^2\phi+k\phi=0\))とすれば、(12)の右辺は0になり、
\[\int_S { (\phi \nabla \psi - \psi \nabla \phi )}\mathrm{d}\boldsymbol{S}= 0 \tag{13}\]
ここで、\(P_0\)を光源、\(P_1\)を観測点、\(Q\)を遮光板の開口部分の1点とし、\(\boldsymbol{r_0}\)を\(P_0\)を原点とした\(Q\)の位置ベクトル、\(\boldsymbol{r_1}\)を\(P_1\)を原点とした\(Q\)の位置ベクトルとする。(図1.1)
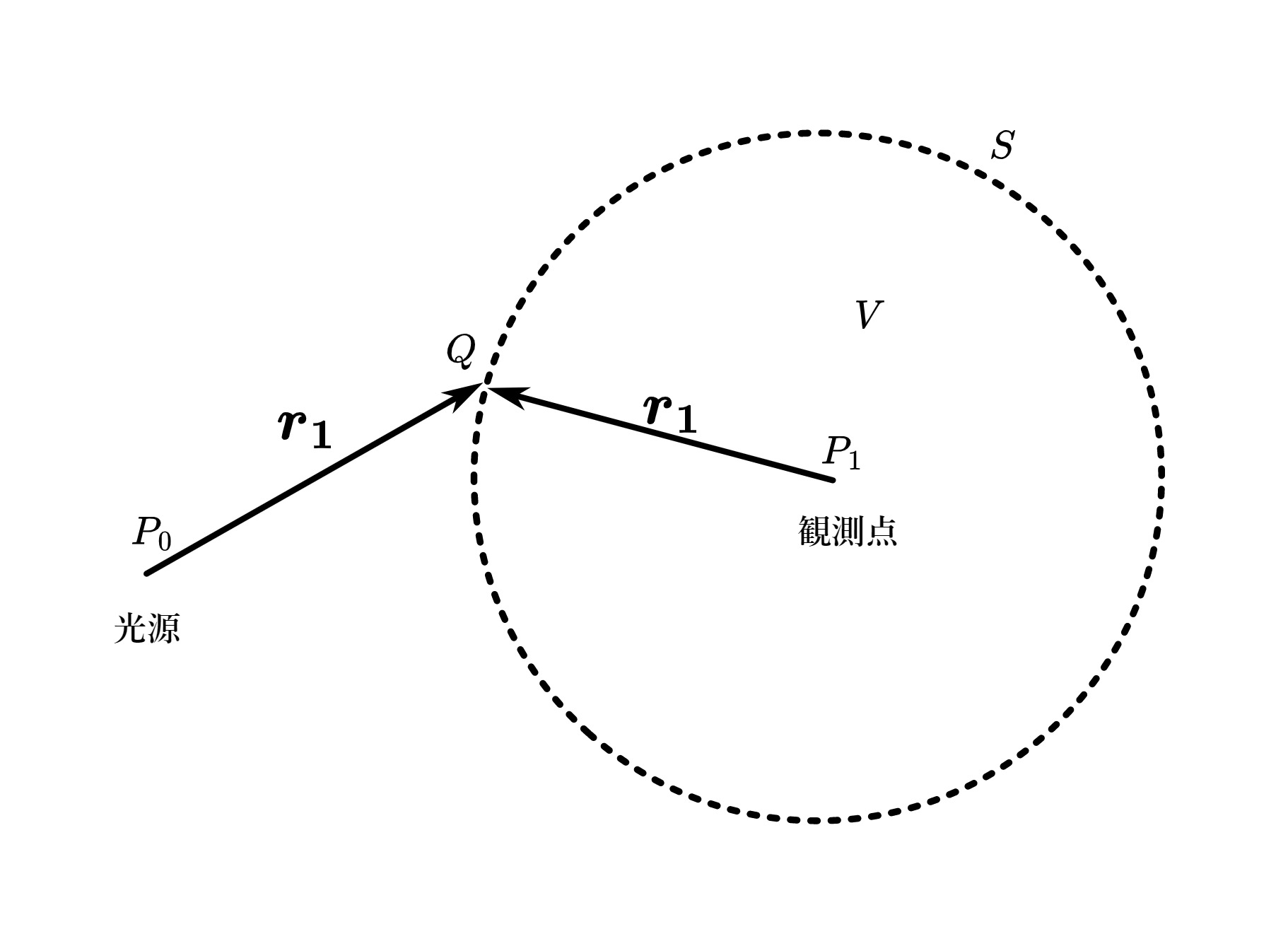
図 1.1
\(u(\boldsymbol{r_0})\)を光源\(P_0\)による、閉曲面上の開口部\(Q\)における電場とする。また、\(v(\boldsymbol{r_1})\)を開口部\(Q\)から観測点\(P_1\)に収束する二次球面波
\[v(\boldsymbol{r_1}) = \frac{ \exp{(-jkr_1)}}{r_1} \tag{14}\]
であると考える。( なお、\(v\)は収束波なので時間項が\(\exp{(j\omega t)}\)であることに注意)
\(u(\boldsymbol{r_0}),v(\boldsymbol{r_1})\)ともにヘルムホルツ方程式を満たす関数であるとはいえ、\(v(\boldsymbol{r_1})\)はそのまま(13)式に適用することはできない(閉空間V内に特異点が生じてしまうため)。ゆえに(13)の左辺を、外側閉曲面\(S\)と、観測点\(P_1\)を中心とする微小半径\(\varepsilon\)の球面\(S'\)についての面積分にわけ、閉空間\(V\)から特異点\(\boldsymbol{r}=0\)を取り除いたのち、\(\varepsilon\rightarrow0\)の極限を取ることを考える。\(P_0\)を原点とする\(R\)の位置ベクトルを\(\boldsymbol{r'_0}\)、\(P_1\)を原点とする\(R\)の位置ベクトルを\(\boldsymbol{r'_1}\)とする(図1.2)。
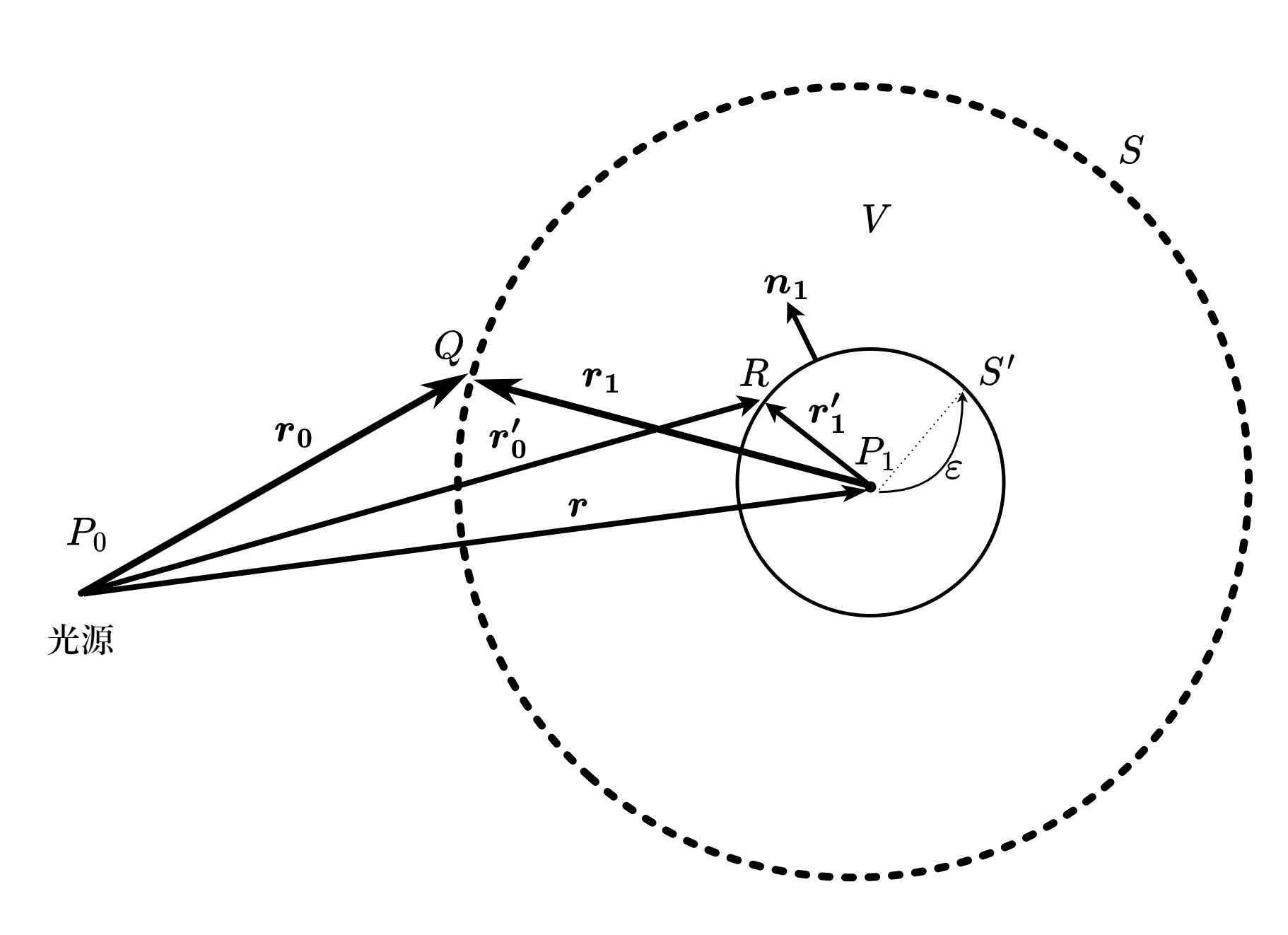
図 1.2
\[\int_S { (\phi \nabla \psi - \psi \nabla \phi) }\mathrm{d}\boldsymbol{S}-\int_{S'} {( \phi' \nabla \psi' - \psi' \nabla \phi' )}\mathrm{d}\boldsymbol{S}=0\tag{15}\]
(15)の\(\phi\)に\(v(\boldsymbol{r_1})\)、\(\phi'\)に\(v(\boldsymbol{r_1'})\)、\(\psi\)に\(u(\boldsymbol{r_0})\)、\(\psi'\)に\(u(\boldsymbol{r'_0})\)をそれぞれ代入する。
\[\int_S { \biggl\{ v(\boldsymbol{r_1})\nabla u(\boldsymbol{r_0}) - u(\boldsymbol{r_0}) \nabla v(\boldsymbol{r_1})\biggr\} }\mathrm{d}\boldsymbol{S}-\int_{S'} {\biggl\{v(\boldsymbol{r'_1}) \nabla u(\boldsymbol{r'_0}) - u(\boldsymbol{r'_0}) \nabla v(\boldsymbol{r'_1}) \biggr\}}\mathrm{d}\boldsymbol{S}=0\]
\[\int_S { \biggl\{ v(\boldsymbol{r_1})\nabla u(\boldsymbol{r_0}) - u(\boldsymbol{r_0}) \nabla v(\boldsymbol{r_1}) \biggr\} }\mathrm{d}\boldsymbol{S}=\int_{S'} {\biggl\{ v(\boldsymbol{r'_1})\nabla u(\boldsymbol{r'_0}) - u(\boldsymbol{r'_0}) \nabla v(\boldsymbol{r'_1}) \biggr\}}\mathrm{d}\boldsymbol{S}\tag{16}\]
\(S, S'\)の外向き法線ベクトルを\(\boldsymbol{n_1}\)とする。ある時刻の電場は球座標系において動径方向距離にのみに依存し、さらに、\(\frac{\partial{\boldsymbol{r}}}{\partial{\boldsymbol{n_1}}}=1\)である。以上から、
\begin{eqnarray} \nabla v &=&\nabla \left\{\frac{ \exp{(-jk\varepsilon)} }{ \varepsilon }\right\}\\ &=&\frac{\partial}{\partial{\varepsilon}} \frac{\exp{(-jk\varepsilon)}}{\varepsilon} \frac{\partial{\boldsymbol{\varepsilon}}}{\partial{\boldsymbol{n_1}}}\\ &=&-\left(jk+\frac{1}{\varepsilon}\right)\frac{\exp{(-jk\varepsilon)}}{\varepsilon} \tag{17} \end{eqnarray}
(16)式の右辺(微小球面\(S'\)についての面積分)に\(v(\boldsymbol{r'_1}), \nabla v(\boldsymbol{r'_1})\)を代入すると
\[\int_{S'} { \biggl\{ \frac{\exp{ (-jk\varepsilon) } }{\varepsilon} \nabla u(\boldsymbol{r'_0})+u(\boldsymbol{r'_0}) \left(jk+\frac{1}{\varepsilon}\right)\frac{\exp{ (-jk\varepsilon) } }{\varepsilon}\biggr\} }\mathrm{d}A\tag{18}\]
球座標の重積分に直す。
\[\int_0^{2\pi}\biggl[\int_{0}^{\pi} { \biggl\{ \frac{\exp{ (-jk\varepsilon) } }{\varepsilon} \nabla u(\boldsymbol{r'_0})+u(\boldsymbol{r'_0}) \left(jk+\frac{1}{\varepsilon}\right)\frac{\exp{ (-jk\varepsilon) } }{\varepsilon} \biggr\} }\varepsilon^2\sin{\theta}\mathrm{d}\theta \biggr]\mathrm{d}\phi\tag{19}\]
\(\varepsilon\rightarrow0\)の極限を取ると、\(r_0'\rightarrow r_0+r_1= r\)に注意して
\begin{eqnarray}\lim_{\varepsilon\rightarrow0}\int_0^{2\pi}\biggl[\int_{0}^{\pi} { \biggl\{ \frac{\exp{ (-jk\varepsilon) } }{\varepsilon} \nabla u(\boldsymbol{r'_0})+u(\boldsymbol{r'_0}) \left(jk+\frac{1}{\varepsilon}\right)\frac{\exp{ (-jk\varepsilon) } }{\varepsilon}\biggr\} }\varepsilon^2\sin{\theta}\mathrm{d}\theta \biggr]\mathrm{d}\phi&=&\int_0^{2\pi}\int_{0}^{\pi} { u(\boldsymbol{r})\sin{\theta}}\mathrm{d}\theta \mathrm{d}\phi\\[17px]&=&4\pi\cdot u(\boldsymbol{r})\tag{20}\end{eqnarray}
従って、(16)式は
\[\int_S { \biggl\{ v(\boldsymbol{r_1}) \nabla u(\boldsymbol{r_0})-u(\boldsymbol{r_0}) \nabla v(\boldsymbol{r_1}) \biggr\} }\mathrm{d}\boldsymbol{S}=4\pi\cdot u(\boldsymbol{r})\]
\[ \therefore u(\boldsymbol{r})=\frac{1}{4\pi}\int_S { \biggl\{ v(\boldsymbol{r_1}) \nabla u(\boldsymbol{r_0})-u(\boldsymbol{r_0}) \nabla v(\boldsymbol{r_1}) \biggr\} }\mathrm{d}\boldsymbol{S}\tag{21}\]
\(v(\boldsymbol{r_1})\)を代入して、
\begin{eqnarray} u(\boldsymbol{r})&=&\frac{1}{4\pi}\int_S { \biggl\{\frac{\exp(-jkr_1)}{r_1} \nabla u(\boldsymbol{r_0})-u(\boldsymbol{r_0}) \nabla \frac{\exp(-jkr_1)}{r_1} \biggr\} }\mathrm{d}\boldsymbol{S}\tag{22}\end{eqnarray}
(22)式がヘルムホルツ・キルヒホフの積分表示である。観測点での電場強度は、それを囲む任意の閉曲面上の電場分布\(u\)と、閉曲面外向き法線方向の微分値により求まることを示している。
1.3 フレネル・キルヒホフの積分表示の導出
無限に広い遮光板に開口部Aが存在し、1次波面を制限しているとする(図1.3)。この状態でヘルムホルツ・キルヒホフの積分表示を適用することを考える。 (23)式の単純閉曲面\(S\)は、\(S=S_1+S_2+A\)と分けることができる。そのうえで、以下のような近似(キルヒホフの近似)を行う[2][3]。
(イ)図中\(S_2\)の積分に対する寄与は、球面半径が非常に大きいと仮定して無視する。(ゾンマーフェルトの放射条件)
(ロ)遮蔽による雑多な影響を全て無視し、開口部における電界は遮蔽板が無いときの値を考える。(キルヒホフの境界条件)
(ハ)遮光板の裏側\(S_1\)での積分も0であると考える。
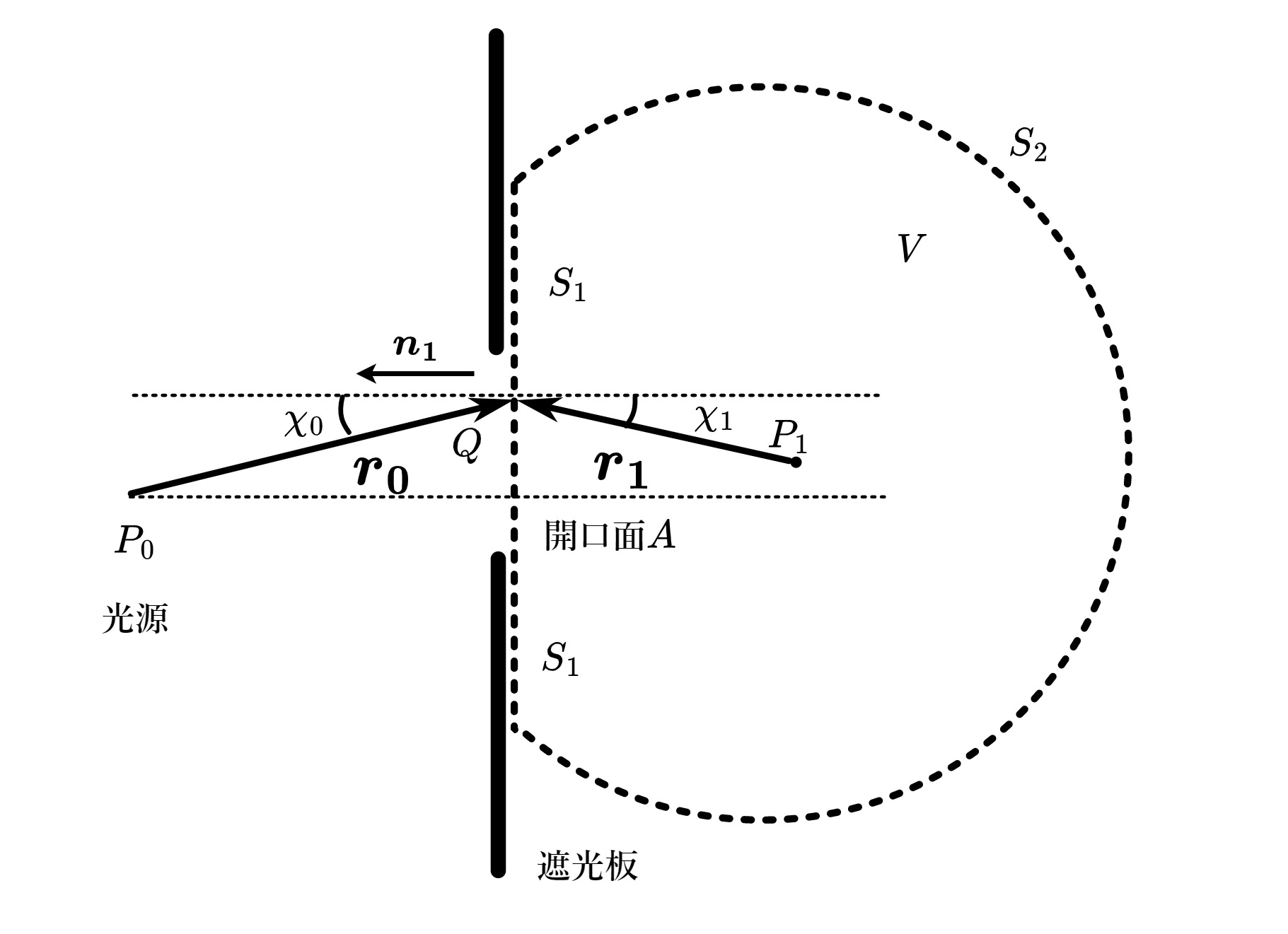
図 1.3
開口部を\(A\)として
\[ u(\boldsymbol{r})=\frac{1}{4\pi}\int_A { \biggl\{ \frac{\exp(-jkr_1)}{r_1} \nabla u(\boldsymbol{r_0})-u(\boldsymbol{r_0}) \nabla \frac{\exp(-jkr_1)}{r_1}\biggr\} }\mathrm{d}\boldsymbol{A}\tag{23}\]
とおく。開口部に図1.3のように法線ベクトル\(\boldsymbol{n_1}\)を立てる。式(23)は、
\[ u(\boldsymbol{r})=\frac{1}{4\pi}\int_A{ \biggl\{ \frac{\exp(-jkr_1)}{r_1}\frac{\partial}{\partial{\boldsymbol{n_1}}} u(\boldsymbol{r_0})-u(\boldsymbol{r_0}) \frac{\partial}{\partial{\boldsymbol{n_1}}} \frac{\exp(-jkr_1)}{r_1}\biggr\} }\mathrm{d}A\tag{24}\]
ここで、\(\frac{\partial}{\partial{\boldsymbol{n_1}}}\)は法線ベクトル\(\boldsymbol{n_1}\)に沿った微分を示す。開口部における電場\(u(\boldsymbol{r_0})\)として波源からの球面波を考え、
\[u(\boldsymbol{r_0}) = A\frac{ \exp{(-jkr_0)}}{r_0} \tag{25}\]
とおく。図1.3に示すように、\(\boldsymbol{n_1}\)とベクトル\(\boldsymbol{r_0}\)のなす角を\(\chi_0\)とすると
\begin{eqnarray}\frac{\partial}{\partial{\boldsymbol{n_1}}} u(\boldsymbol{r_0}) &=&A \frac{\partial}{\partial{\boldsymbol{n_1}}}\frac{ \exp{(-jkr_0)}}{r_0} \\ &=& A \frac{\partial}{\partial{\boldsymbol{r_0}}}\left\{\frac{ \exp{(-jkr_0)}}{r_0}\right\} \frac{\partial{\boldsymbol{r_0}}}{\partial{\boldsymbol{n_1}}} \\&=& A\left(-jk-\frac{1}{r_0}\right)\frac{ \exp{(-jkr_0)}}{r_0}(-\cos{\chi_0})\\&=& A\left(jk+\frac{1}{r_0}\right)\frac{ \exp{(jkr_0)}}{r_0}\cos{\chi_0} \tag{26}\end{eqnarray}
(ここでの\(\frac{\partial{\boldsymbol{r_0}}}{\partial{\boldsymbol{n_1}}} \)は\(\boldsymbol{r_0}\)が\(\boldsymbol{n_1}\)に正対する割合を示し、両ベクトルの方向余弦である。)
波長\(\lambda\)が\(\boldsymbol{r_0}\)の大きさより十分に小さい、つまり\(k\gg\frac{1}{r_0}\)とすれば、(26)式は
\[\frac{\partial}{\partial{\boldsymbol{n_1}}} u(\boldsymbol{r_0})\approx jkA\cos{\chi_0}\frac{ \exp{(-jkr_0)}}{r_0} \tag{27} \]
また、\(\boldsymbol{n_1}\)とベクトル\(\boldsymbol{r_1}\)のなす角を\(\chi_1\)とすると
\begin{eqnarray}\frac{\partial}{\partial{\boldsymbol{n_1}}} \frac{\exp(-jkr_1)}{r_1} &=& \frac{\partial}{\partial{\boldsymbol{r_1}}}\left\{\frac{ \exp{(-jkr_1)}}{r_1}\right\} \frac{\partial{\boldsymbol{r_1}}}{\partial{\boldsymbol{n_1}}} \\&=& -\left(jk+\frac{1}{r_1}\right)\frac{ \exp{(-jkr_1)}}{r_1}(-\cos{\chi_1})\\&=& \left(jk+\frac{1}{r_1}\right)\frac{ \exp{(-jkr_1)}}{r_1}\cos{\chi_1} \tag{28}\end{eqnarray}
波長\(\lambda\)が\(\boldsymbol{r_1}\)の大きさより十分に小さいとすると、
\[\frac{\partial}{\partial{\boldsymbol{n_1}}} \frac{\exp(-jkr_1)}{r_1} \approx jk\cos{\chi_1}\frac{ \exp{(-jkr_1)}}{r_1} \tag{29} \]
(25)、(27)、(29)を(24)へ代入する。
\begin{eqnarray} u(\boldsymbol{r})&=&\frac{1}{4\pi}\int_A{ \biggl\{ \frac{\exp(-jkr_1)}{r_1}\frac{\partial}{\partial{\boldsymbol{n_1}}} u(\boldsymbol{r_0})-u(\boldsymbol{r_0}) \frac{\partial}{\partial{\boldsymbol{n_1}}} \frac{\exp(-jkr_1)}{r_1}\biggr\} }\mathrm{d}A\\ &=&\frac{1}{4\pi}\int_A{ \biggl[ \frac{\exp(-jkr_1)}{r_1}\biggl\{jkA\cos{\chi_0}\frac{ \exp{(-jkr_0)}}{r_0}\biggl\}-A\frac{ \exp{(-jkr_0)}}{r_0} \biggl\{ jk\cos{\chi_1}\frac{ \exp{(-jkr_1)}}{r_1}\biggr\}\biggr] }\mathrm{d}A\\ &=& \frac{jkA}{4\pi} \int_{A}\biggl[ \frac{\exp{\{-jk(r_0+r_1)\}}}{r_0 r_1}\frac{\cos{\chi_0}-\cos{\chi_1}}{2}\biggr]\mathrm{d}A\\&=& \frac{jA}{\lambda}\int_{A}\frac{\exp{\{-jk(r_0+r_1)\}}}{r_0 r_1}\frac{\cos{\chi_0}-\cos{\chi_1}}{2}\mathrm{d}A\tag{30}\end{eqnarray}
(30)式は、遮蔽板の開口部における回折を考えるため、ヘルムホルツ・キルヒホフの積分表示に対してキルヒホフの近似を加味することで得られた積分であり、フレネル・キルヒホフの積分表示という。
1.4 近軸近似
さらに、図1.3における角度\(\chi_0\)が非常に小さい、つまり光線が回折系の光軸に近いと仮定する(近軸近似)。そのとき、光軸と直線\(P_0 P_1\)(ベクトル\(\boldsymbol{r}\))のなす角を\(\delta\)とれば、\(\cos{\chi_0}\approx -\cos{\chi_1}\approx\cos{\delta}\)が成り立つので、(30)式は
\[u(\boldsymbol{r}) = \frac{jA\cos{\delta}}{\lambda}\int_{A}\frac{\exp{\{-jk(r_0+r_1)\}}}{r_0 r_1}\mathrm{d}A\tag{31}\]
と書ける。
さらに、光源\(P_0\)と観測点\(P_1\)が開口部\(A\)から遠く離れており、かつ光軸に十分近い場合、\(\cos{\delta}\approx1\)と考えてよいから、
\[u(\boldsymbol{r}) = \frac{jA}{\lambda}\int_{A}\frac{\exp{\{-jk(r_0+r_1)\}}}{r_0 r_1}\mathrm{d}A\tag{32}\]
となる。
1.5 開口関数とフレネル近似
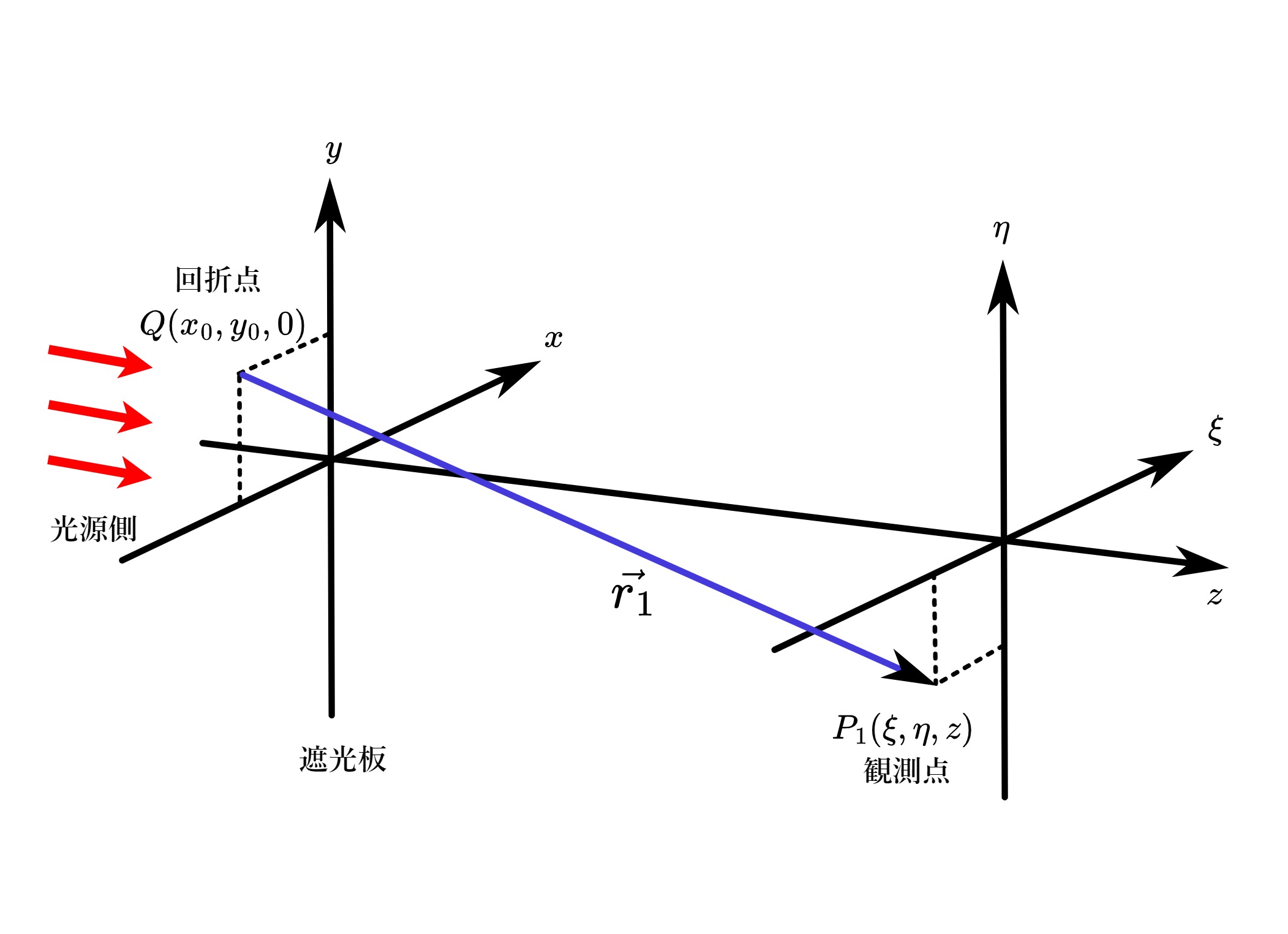
図 1.4
あらたに、図1.4のごとく座標系をとる。いま、点光源は左側遠方にあり、開口部の広がりも光源や観測点のz軸からの距離も、観測点と開口部との距離\(z\)に比べ十分小さいとする。さすれば式(32)は
\[u(\xi,\eta;z) = \frac{jA}{\lambda}\int_{A}\frac{\exp{\{-jk(r_0+r_1)\}}}{r_0 r_1}\mathrm{d}x_0 \mathrm{d}y_0\tag{33}\]
となる。
ここで、開口部の複素透過率を表す関数(開口透過率)\(g(x_0,y_0)\)を導入する。ただし、開口部内では\(g(x_0,y_0)=|g(x_0,y_0)|\exp{j \phi_g (x_0,y_0)}\)、開口部外の遮蔽領域では\(g(x_0,y_0)=0\)とする\(|g(x_0,y_0)|\)は開口部の振幅透過率、\(\phi_g (x_0,y_0)\)は開口部の位相透過率)。開口透過率の導入により積分範囲を拡張すると、
\[u(\xi,\eta;z) = \frac{jA}{\lambda}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x_0,y_0)\frac{\exp{\{-jk(r_0+r_1)\}}}{r_0 r_1}\mathrm{d}x_0 \mathrm{d}y_0\tag{34}\]
さらに、開口部透過直後の複素振幅分布を開口関数\(u(x_0,y_0)\)として定義する。以後この\(u(x_0,y_0)\)に電場の次元を持たせることにする。これまでの議論通り、波源から開口部への入射光が球面波なら
\[u(x_0,y_0)_{spherical}= g(x_0,y_0)A\frac{\exp{-jkr_0}}{r_0}\tag{35}\]
で、もし平面波であるならば
\[u(x_0,y_0)_{planar}= g(x_0,y_0)A\tag{36}\]
である。
この開口関数を使用して式(34)を書き改めると
\[u(\xi,\eta;z) = \frac{j}{\lambda}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}u(x_0,y_0)\frac{\exp{(-jkr_1)}}{r_1}\mathrm{d}x_0 \mathrm{d}y_0\tag{37}\]
となる。
伝播距離
\[r_1=\sqrt{z^2+(\xi-x_0)^2+(\eta-y_0)^2}=z\sqrt{1+\left(\frac{\xi-x_0}{z}\right)^2+\left(\frac{\eta-y_0}{z}\right)^2}\tag{38}\]
は、近軸の仮定\(\xi-x_0\approx\eta-y_0\approx0\)から次のように展開できる。
\[r_1=z+\frac{1}{2z}\left\{\left(\xi-x_0\right)^2+\left(\eta-y_0\right)^2\right\}+\frac{1}{8z^3}\left\{\left(\xi-x_0\right)^2+\left(\eta-y_0\right)^2\right\}^2+...\tag{39}\]
ここで、式(39)において第2項(\(\xi,\eta\)の2乗項)までで近似的に表せる領域をフレネル領域といい、その近似をフレネル近似という。(\(\xi,\eta\)の1乗項で十分な領域をフラウンホーファー領域という)
フレネル領域の条件は、第3項での位相回転が\(2\pi\)より十分小さいこと、つまり
\[z^3\ll\frac{1}{8\lambda}\left\{\left(\xi-x_0\right)^2+\left(\eta-y_0\right)^2\right\}_{\max}^2\tag{40}\]
の形で与えられる[1]。
観測点のz座標が式(40)の条件を満たすとする。\(1/r\approx1/z\)と近似したのち、式(39)の第2項までを式(37)に代入すると、
\[u(\xi,\eta;z) = \frac{j}{\lambda}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}u(x_0,y_0)\frac{\exp{\left[-jk\left\{z+\frac{\left(\xi-x_0\right)^2}{2z}+\frac{\left(\eta-y_0\right)^2}{2z}\right\}\right]}}{z}\mathrm{d}x_0 \mathrm{d}y_0\]
整理すると、
\[u(\xi,\eta;z) = \frac{j}{\lambda}\frac{\exp{(-jkz)}}{z}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}u(x_0,y_0)\exp{\left[-jk\left\{\frac{\left(\xi-x_0\right)^2}{2z}+\frac{\left(\eta-y_0\right)^2}{2z}\right\}\right]}\mathrm{d}x_0 \mathrm{d}y_0\tag{41}\]
式(41)が、フレネル領域における回折光の振幅分布の式である。
1.6 フレネル積分
ひとまず矩形開口部を考え、\(x\)軸方向が幅\(2L_x\)、\(y\)軸方向の幅は\(2L_y\)とし、開口部重心が座標原点にあるとする。また、観測点の座標を\((x,y,z)=(\xi,0,z)\)とし、開口関数\(u(x_0,y_0)\)の値は実定数\(U_0\)[V/m]であるとする。\(z\)はパラメータとして扱う。(41)式を書き直すと、
\begin{eqnarray}u(\xi) &=& \frac{jU_0}{\lambda}\frac{\exp{(-jkz)}}{z}\int_{-L_x}^{L_x}\int_{-L_y}^{L_y}\exp{\left[-jk\left\{\frac{\left(\xi-x_0\right)^2}{2z}+\frac{\left(\eta-y_0\right)^2}{2z}\right\}\right]}\mathrm{d}y_0 \mathrm{d}x_0\tag{42}\end{eqnarray}
ここで、積分内のexpをオイラーの公式で展開して\(\sin,\cos\)で表現してみると
\[u(\xi) = \frac{jU_0}{\lambda}\frac{\exp{(-jkz)}}{z}\int_{-L_x}^{L_x}\int_{-L_y}^{L_y}\left[\cos{\left\{k\frac{\left(\xi-x_0\right)^2}{2z}+k\frac{\left(\eta-y_0\right)^2}{2z}\right\}}-j\sin{\left\{k\frac{\left(\xi-x_0\right)^2}{2z}+k\frac{\left(\eta-y_0\right)^2}{2z}\right\}}\right]\mathrm{d}y_0 \mathrm{d}x_0 \tag{43}\]
となり、\(\cos\)や\(\sin\)の内部に積分変数の2乗が現れていることがわかる。これが解析的に解けないことで有名な「(正規化)フレネル積分」である。
\[S(x)=\int_0^x \sin{\left(\frac{\pi}{2} t^2\right)}\mathrm{d}t\tag{44}\]
をフレネル正弦積分、
\[C(x)=\int_0^x \cos{\left(\frac{\pi}{2} t^2\right)}\mathrm{d}t\tag{45}\]
をフレネル余弦積分という。その最大値は1を超えない。グラフを図1.5に示す。
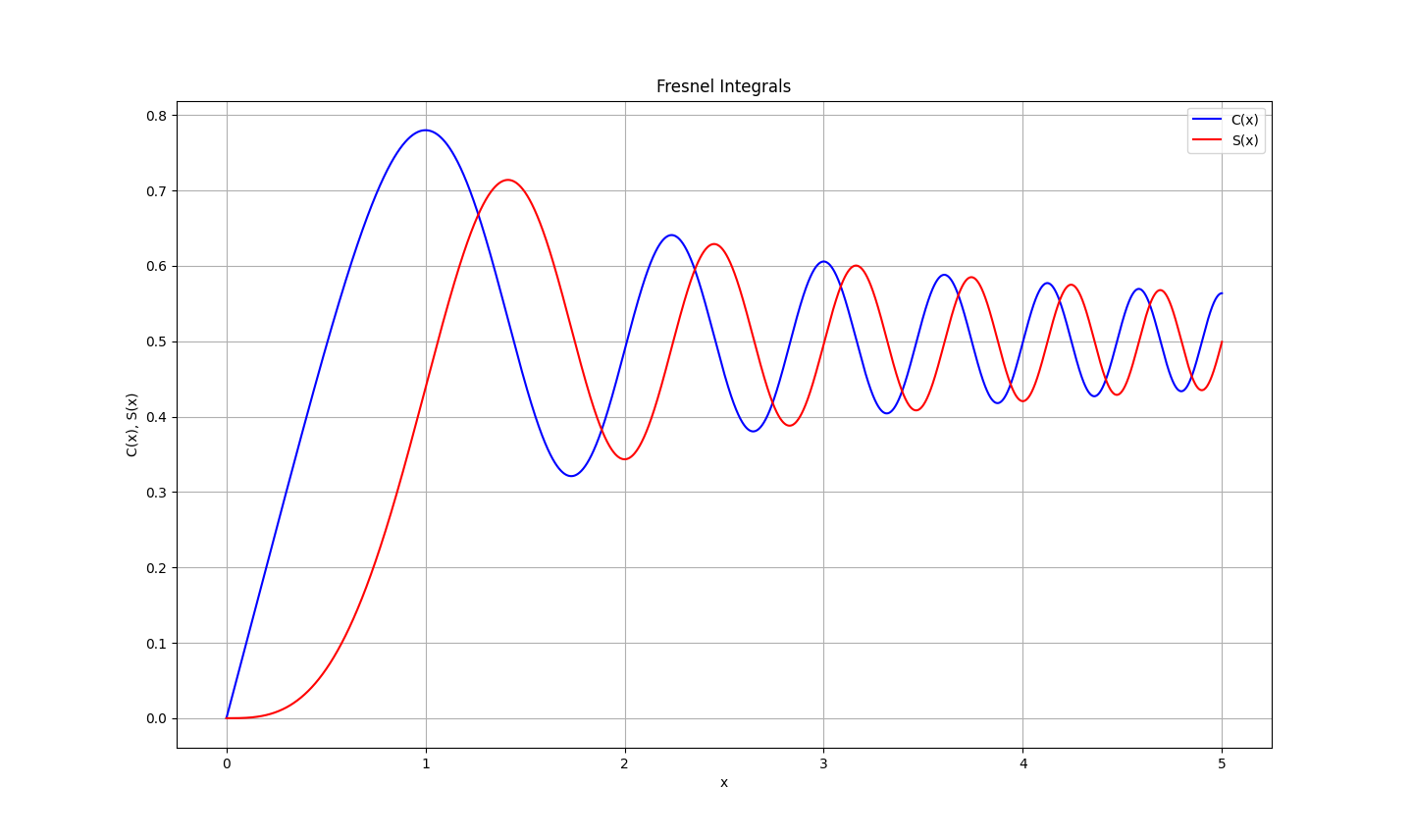
図1.5 フレネル積分のグラフ
フレネル積分には、
\[C(-x)=-C(x),\quad S(-x)=-S(x)\tag{46}\]
なる関係がある。被積分関数は減衰せず振動する関数だが、その積分は
\[C(\infty)=\frac{1}{2},\quad S(\infty)=\frac{1}{2}\tag{47}\]
と、有限値に収束する(証明は省く)。これらの事実を認めると、
\[\int_0^x \exp{\left(j\frac{\pi}{2} t^2\right)}\mathrm{d}t=\int_0^x \cos{\left(\frac{\pi}{2} t^2\right)}\mathrm{d}t+j\int_0^x \cos{\left(\frac{\pi}{2} t^2\right)}\mathrm{d}t\tag{48}\]
であるから、(46)式と併せて、
\[\int_{0}^{\infty} \exp{\left(j\frac{\pi}{2} t^2\right)}\mathrm{d}t=\int_{-\infty}^{0} \exp{\left(j\frac{\pi}{2} t^2\right)}\mathrm{d}t=\frac{1}{2}+\frac{1}{2}j\tag{49}\]
\[\int_{-\infty}^{\infty} \exp{\left(\frac{\pi}{2} t^2\right)}\mathrm{d}t=1+j\tag{48}\]
が成り立つことがわかる。
式(42)をフレネル積分で表すため、
\[\frac{k}{2z}(\xi-x_0)^2=\frac{\pi}{2}t^2\tag{50}\]
となる変数変換(\(x_0\rightarrow t\))を施す。\(t=\sqrt{\frac{k}{2\pi}}(\xi-x_0)=\sqrt{\frac{2}{z\lambda}}(\xi-x_0)\)であるから、\(\mathrm{d}x_0=-\sqrt{\frac{z\lambda}{2}}\mathrm{d}t\)で、積分範囲は\(\sqrt{\frac{2}{z\lambda}}(\xi-L_x)\equiv t_2\)、\(\sqrt{\frac{2}{z\lambda}}(\xi+L_x)\equiv t_1\)と書き換わる。
積分変数\(y_0\)についても\(x_0\)と同様の変換(\(y_0\rightarrow s\))を行えば、\(s=\sqrt{\frac{2}{z\lambda}}(\eta-y_0)\)、\(\mathrm{d}y_0=-\sqrt{\frac{z\lambda}{2}}\mathrm{d}s\)となり、積分範囲は\(\sqrt{\frac{2}{z\lambda}}(\xi-L_y)\equiv s_2\)、\(\sqrt{\frac{2}{z\lambda}}(\xi+L_y)\equiv s_1\)に書き換わる。
しからば(42)式は
\begin{eqnarray}u(\xi) &=& \frac{jU_0}{\lambda}\frac{\exp{(-jkz)}}{z}\int_{-L_y}^{L_y}\int_{-L_x}^{L_x}\left[\cos{\left\{k\frac{\left(\xi-x_0\right)^2}{2z}+k\frac{\left(\eta-y_0\right)^2}{2z}\right\}}-j\sin{\left\{k\frac{\left(\xi-x_0\right)^2}{2z}+k\frac{\left(\eta-y_0\right)^2}{2z}\right\}}\right]\mathrm{d}x_0 \mathrm{d}y_0 \\ &=& \frac{jU_0\exp{(-jkz)}}{2}\int_{s_1}^{s_2}\int_{t_1}^{t_2}\left\{\cos{\left(\frac{\pi}{2}t^2+\frac{\pi}{2}s^2\right)}-j\sin{\left(\frac{\pi}{2}t^2+\frac{\pi}{2}s^2\right)}\right\}\mathrm{d}t\mathrm{d}s \\ &=& \frac{jU_0\exp{(-jkz)}}{2}\int_{s_1}^{s_2}\int_{t_1}^{t_2}\left[\left\{\cos{\left(\frac{\pi}{2}t^2\right)}\cos{\left(\frac{\pi}{2}s^2\right)}-\sin{\left(\frac{\pi}{2}t^2\right)}\sin{\left(\frac{\pi}{2}s^2\right)}\right\}-j\left\{\sin{\left(\frac{\pi}{2}t^2\right)}\cos{\left(\frac{\pi}{2}s^2\right)}+\cos{\left(\frac{\pi}{2}t^2\right)}\sin{\left(\frac{\pi}{2}s^2\right)}\right\}\right]\mathrm{d}t\mathrm{d}s \\ &=&\frac{jU_0\exp{(-jkz)}}{2}\biggl[ \bigr\{\bigl(C(t_2)-C(t_1)\bigr)\bigl(C(s_2)-C(s_1)\bigr)-\bigl(S(t_2)-S(t_1)\bigr)\bigl(S(s_2)-S(s_1)\bigr)\bigr\}\\&&-j\bigl\{\bigl(S(t_2)-S(t_1)\bigr)\bigl(C(s_2)-C(s_1)\bigr)+\bigl(C(t_2)-C(t_1)\bigr)\bigl(S(s_2)-S(s_1)\bigr)\bigr\} \biggr]\tag{51}\end{eqnarray}
となる。\(t,s\)は無次元であるから、積分内も無次元となるが、式(51)自体の次元は\(U_0\)の次元、つまり電場[V/m]の単位を持ったままである。ただ、積分に掛かる係数に\(z,\lambda\)のようなパラメータが消え、それらの寄与は全て積分変数\(s,t\)に押し付けられている。次元はそのまま、パラメータを1箇所に集約できたので解析が楽になることは言うまでもないだろう。
1.7 無限長スリット
開口部が\(y\)軸方向に無限の長さを持つスリットであると仮定する。\(L_y\rightarrow \infty\)で\(s_2\rightarrow -\infty , s_1\rightarrow \infty\)に注意して(47)式を書き改めれば、
\begin{eqnarray}u(\xi) &=&\frac{jU_0\exp{(-jkz)}}{2} \biggl[ \bigr\{\bigl(C(t_2)-C(t_1)\bigr)\bigl(C(-\infty)-C(\infty)\bigr)-\bigl(S(t_2)-S(t_1)\bigr)\bigl(S(-\infty)-S(\infty)\bigr)\bigr\}\\&&-j\bigl\{\bigl(S(t_2)-S(t_1)\bigr)\bigl(C(-\infty)-C(\infty)\bigr)+\bigl(C(t_2)-C(t_1)\bigr)\bigl(S(-\infty)-S(\infty)\bigr)\bigr\} \biggr] \\&=&\frac{jU_0\exp{(-jkz)}}{2} \biggl[ \bigl\{-C(t_2)+C(t_1)+S(t_2)-S(t_1)\bigr\}+j\bigl\{C(t_2)-C(t_1)+S(t_2)-S(t_1)\bigr\} \biggr]\tag{52} \end{eqnarray}
光強度分布を得るには、電場の複素振幅の絶対値をとり、2乗する。\(c\rm{[m/s]}\)を光速、\(\varepsilon_0\rm{[F/m]}\)を真空の誘電率とすると、光の強度(=エネルギー面密度)\(i\rm{[W/m^2]=[J\cdot s/m^2]}\)は、
\begin{eqnarray}i(\xi)=\frac{1}{2}c\varepsilon_0 |u(\xi)|^2 &=&\frac{c\varepsilon_0 {U_0}^2}{8}\biggl[ \bigl\{-C(t_2)+C(t_1)+S(t_2)-S(t_1)\bigr\}^2+\bigl\{C(t_2)-C(t_1)+S(t_2)-S(t_1)\bigr\}^2 \biggr] \tag{53}\end{eqnarray}
この(53)式は以下の定積分を書き下したものに等しい。
\[ i(\xi) =\frac{c\varepsilon_0 {U_0}^2}{8} \biggl[ \biggl\{\int_{t_1}^{t_2}\bigl\{\sin{\left(\frac{\pi}{2}t^2\right)}-\cos{\left(\frac{\pi}{2}t^2\right)}\bigr\}\mathrm{d}t\biggr\}^2+\biggl\{\int_{t_1}^{t_2}\bigl\{\sin{\left(\frac{\pi}{2}t^2\right)}+\cos{\left(\frac{\pi}{2}t^2\right)}\bigr\}\mathrm{d}t\biggr\}^2 \biggr]\tag{54} \]
デジタル計算機で数値シミュレーションを行う場合、フレネル積分を計算するライブラリがあるなら(53)式が扱いやすいだろう。
2. アナログコンピュータプログラム
今回扱う式はそこまで複雑ではないのだが、扱う定係数の桁に幅がありすぎることが(ダイナミックレンジの制限がデジタルより厳しい)アナログコンピュータでの実行を難しくしている。また、導出途中で積分変数(すなわちアナログコンピュータ上の独立変数)に対して変数変換を行っており、その変換を演算回路にどう反映するかも悩みの種である。通常と異なり実装する式が微分方程式ではないため、時間積分が陽に出現しており、いつもは気にすることのない「時間定積分を積分器でどう実現するか」にも気を配らねばならない。
その一方で、フレネル積分のスケール自体は既知であり、収束するという性質もわかっているから、定係数の扱いや、独立変数の調整にさえ十分注意すれば全体の見通しは立てやすいだろう。
求めたいのは回折光の強度分布\(i(\xi)\rm{[W/m^2]}\)と観測点のx座標\(\xi\rm{[m]}\)の関係であり、\(\xi=[-0.01\rm{[m]}, 0.01\rm{[m]}]\)の範囲とする。とりあえず波長\(\lambda\)は500 nmにして、回折点と観測点の距離\(z\)を可変パラメータ(係数ポテンショメータで調整できる係数)としたい。スリットも\(L_x\equiv L=0.005\)mで固定とする。アナログコンピュータのマシンユニットは10Vで、低速モードに設定し、1rad/s以下の超低周波で精密演算をおこなえるよう時間換算するものとする。XYレコーダのy軸に光強度\(i\)に電圧換算を施した電圧信号\(I\)を、x軸には、観測点x座標\(\xi\)に比例する電圧信号\(\Xi\)を入力し、両者の関係を記録する。
2.1 フレネル積分の変形
さっそく第1章の過程を否定するようで申し訳ないが、被積分関数が\(\sin{\left(\frac{\pi}{2}t^2\right)},\cos{\left({\frac{\pi}{2}t^2}\right)}\)である必要はない。前章の導出ではこのようなフレネル積分の定義を出現させ、デジタルシミュレーションが容易になるように変数変換を施したわけだが(実際数多の参考文献でこの変換が書かれている)、アナログコンピュータでシミュレーションする上ではあまり意味のないことである。むしろ、\(\sin\)等の中身を定係数なしの単純な形にした方が、変数の電圧換算が容易になる。
なので、(43)式までさかのぼり、正規化されていないフレネル積分
\[\mathscr{S}(x)\equiv \int_{0}^{x}\sin{(t^2)}\mathrm{d}t\tag{55}\]
\[\mathscr{C}(x)\equiv \int_{0}^{x}\cos{(t^2)}\mathrm{d}t\tag{56}\]
が現れるように新たな変数変換を施す。
\[\mathscr{S}(\infty)=\mathscr{C}(\infty)=\frac{1}{2}\sqrt{\frac{\pi}{2}}\tag{57}\]
が成り立つ。また、最大値は1を超えない。(スケーリングが楽になるので大変有難い。)
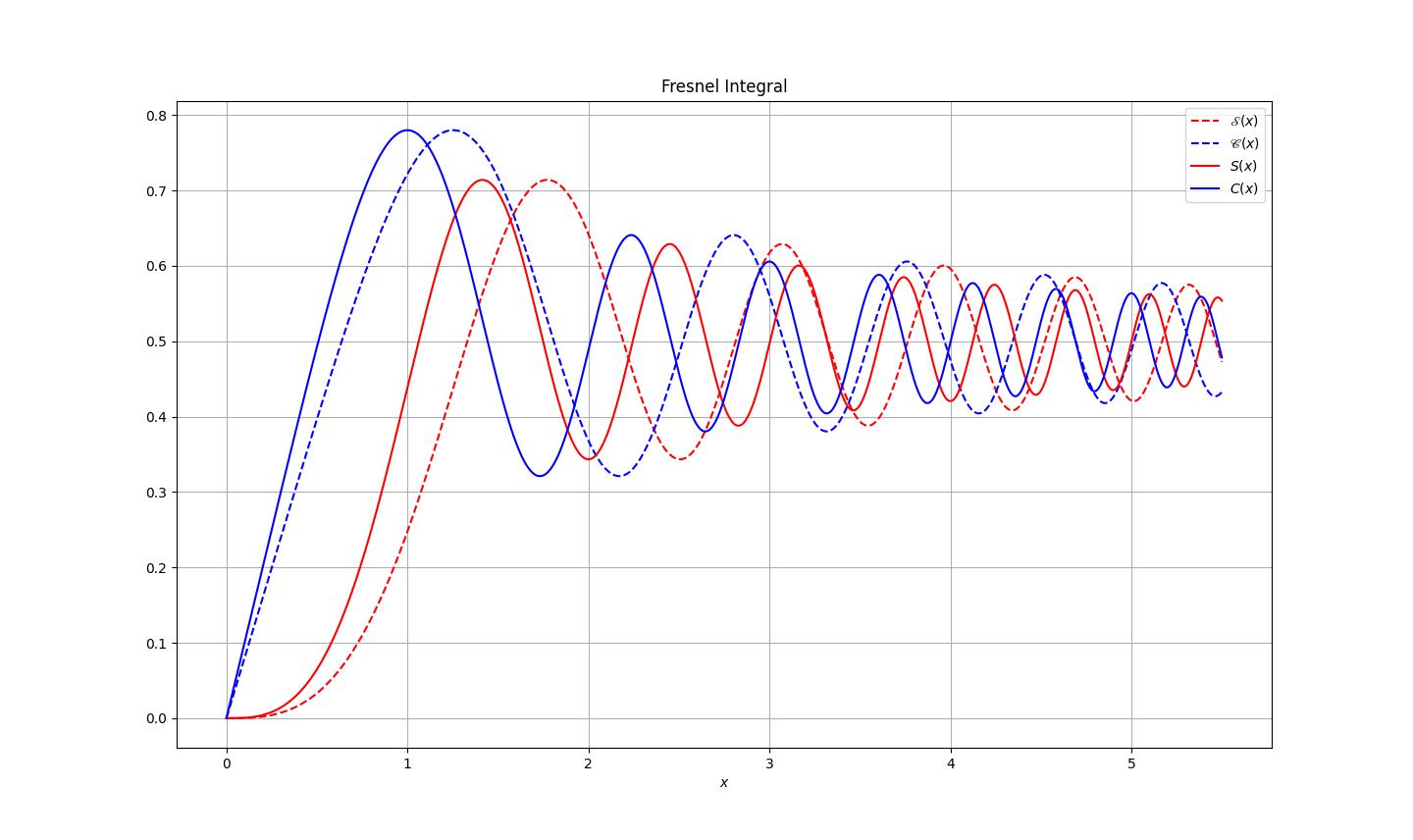
図 2.1 フレネル積分のグラフ(破線が\(\mathscr{S}(x), \mathscr{C}(x)\))
この変形(?)フレネル積分をもとに光強度の式を書き直したい。\(t\)のかわりにとして
\[\sqrt{\frac{\pi}{z\lambda}}(\xi-x_0)\equiv p\tag{58}\]
なる変数を導入すると、
\[\mathrm{d}x_0=-\sqrt{\frac{z\lambda}{\pi}}\mathrm{d}p\tag{59}\]
\[p_1=\sqrt{\frac{\pi}{z\lambda}}(\xi+L)\tag{60}\]
\[p_1=\sqrt{\frac{\pi}{z\lambda}}(\xi-L)\tag{61}\]
電場の複素振幅は、
\begin{eqnarray} u(\xi)&=&\frac{jU_0\exp{(-jkz)}}{\pi} \biggl[ \bigl\{-\mathscr{C}(p_2)+\mathscr{C}(p_1)+\mathscr{S}(p_2)-\mathscr{S}(p_1)\bigr\}+j\bigl\{\mathscr{C}(p_2)-\mathscr{C}(p_1)+\mathscr{S}(p_2)-\mathscr{S}(p_1)\bigr\} \biggr]\tag{62}\end{eqnarray}
光強度は、
\[i(\xi)=\frac{1}{2}c\varepsilon_0 |u(\xi)|^2 =\frac{c\varepsilon_0 {U_0}^2}{2\pi}\biggl[ \bigl\{-\mathscr{C}(p_2)+\mathscr{C}(p_1)+\mathscr{S}(p_2)-\mathscr{S}(p_1)\bigr\}^2+\bigl\{\mathscr{C}(p_2)-\mathscr{C}(p_1)+\mathscr{S}(p_2)-\mathscr{S}(p_1)\bigr\}^2 \biggr] \tag{63}\]
これが無限長スリットの場合にアナログコンピュータで演算する式とする。
定積分の形に戻してみると、
\[ i(\xi) =\frac{c\varepsilon_0 {U_0}^2}{2\pi} \biggl[ \biggl\{\int_{p_1}^{p_2}\bigl\{\sin{\left(p^2\right)}-\cos{\left(p^2\right)}\bigr\}\mathrm{d}p\biggr\}^2+\biggl\{\int_{p_1}^{p_2}\bigl\{\sin{\left(p^2\right)}+\cos{\left(p^2\right)}\bigr\}\mathrm{d}p\biggr\}^2 \biggr]\tag{64} \]
となる。
2.2 定係数の対処
(1) 定係数\(\frac{c\varepsilon_0 {U_0}^2}{2\pi}\)
(63)式から、基本的に
\[(光強度 i )=(定係数\frac{c\varepsilon_0 {U_0}^2}{2\pi})\times({フレネル積分の2乗式})\tag{65}\]
であると考えてよい。ひとまずこの定係数を\(A_0 \rm{[W/m^2]}\)と置こう。
\(U_0\rm{[V/m]}\)の相場が分からないのだが、実際SI単位系で開口部の電場振幅を表すとかなり小さな値になると思うし、回路の後段にその都度100倍、1000倍の増幅を行うブロックを付加し強度振幅を拡大することは容易ではあるものの、あまりにも微小な電圧が演算信号として扱われるとS/N比的にもあまり宜しくない。ゆえに、XYレコーダの\(y\)軸に入力する信号を\(i/A_0\)の信号とすることが一番手っ取り早い解決策に思える。あとで値を読み取りたいときは、\(U_0\)の値に応じて、\(A_0\)を乗じた値を読み取ればよいだろう。
(2)係数\(\sqrt{\frac{2}{z\lambda}}\)中の波長\(\lambda\)について
もう一つ厄介なものが、積分変数を無次元にするための変数変換
\[p=\sqrt{\frac{\pi}{z\lambda}}(\xi-x_0)\]
に登場した係数\(\sqrt{\frac{\pi}{z\lambda}}\)である。\(z\)はともかく、波長を係数器で設定することは、その桁数から見ても事実上不可能である。
ためしに係数に\(\lambda=5\times10^{-7}\)を代入してみると、
\[\sqrt{\frac{\pi}{z\lambda}}=\sqrt{\frac{2\pi}{z}}\times 10^{3}\fallingdotseq \frac{2.507}{\sqrt{z}}\times 10^{3}\tag{66}\]
となる。式(63)からわかる通り、演算回路で実際に電圧信号として現れるものは\(p_1,p_2\)(厳密には\(p_1^{2},p_2^{2}\)の微分値である\(2p_1,2p_2\))に限られ、なおかつそれは独立変数\(\xi\)の関数といえる。
\[p_1=\sqrt{\frac{\pi}{z\lambda}}(\xi+L)\fallingdotseq \frac{2.507}{\sqrt{z}}\times 10^{3}(\xi+L)\tag{67}\]
\(z\)の最小値が1[m]、\(\xi\)の最大値が\(10^{-2}\)[m]、\(L=5\times 10^{-3}\)[m]であることを考えれば、\(|2p_1|\)は高々80、同様に\(|2p_2|\)の最大値も80弱になることがわかる。
このことから、非常に小さい値である真の独立変数\(\xi\)を電圧で実現するのではなく、最初から演算回路の出発点として変数\(p\)を選べばよいだろう。(回路的には、XYレコーダのx軸に入力する\(\Xi\)は\(p\)をもとに作る。演算理論に厳密になるなら全電圧信号は演算時間\(\tau\)による積分により生成するべきではあるが、なにしろ積分器がもったいないので。)
そうすると、係数\(\sqrt{\frac{\pi}{z\lambda}}\)は直接的に係数ポテンショメータで設定する値ではなくなるので、スケーリングは考えなくて良い。また、信号\(2p_1,2p_2\)については80を1MU(=10V)とするように電圧換算係数を定めればよいことがわかる。
2.3 スケーリングとブロックダイヤグラム
原変数のフロー概略図を図1.7に示す。
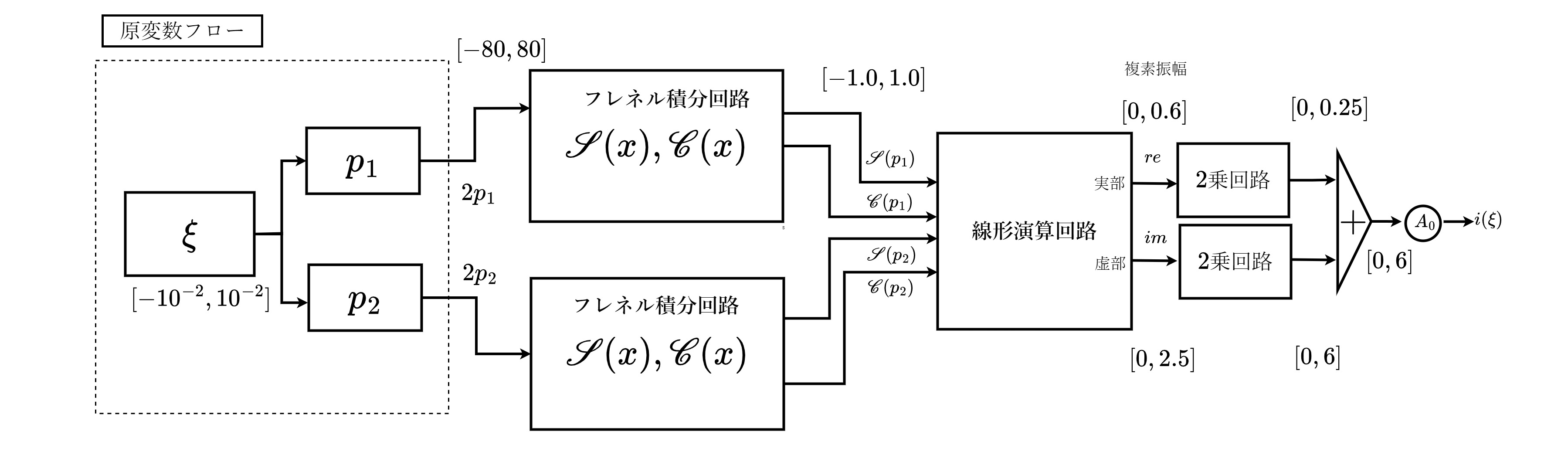
図2.2 原変数フロー図
[ ]内はおおよその値域である。スケーリングの目安となる。今回は微分方程式ではないので変数間のフィードバックが存在しない。(ただしフレネル積分のブロック内では微分方程式を解く必要がありループが形成される。)
原変数上では\(\xi\)をもとに\(p\)(ただ単に\(p\)と言うときは\(2p_1,2p_2,2p_0\)などの信号を指すものとする)を生成するような流れになるが、演算回路では定数積分により\(p\)を生成するのが先であることに注意。\(p\)は時間比例信号ではあるものの、独立変数ではないので\(a_B\)による換算は必要とせず、\(a_\tau,a_P\)のみ作用させればいい。つまり、原方程式
\[\frac{\mathrm{d}p}{\mathrm{d}\xi}=\frac{2\sqrt{2\pi}\times{15}}{\sqrt{z}10^{-2}}=7.5198...\times 10^{3}/\,\sqrt{z}\quad(\rightarrow{p-\xiグラフの傾き})\tag{68}\]
を立て、
\[\frac{a_\tau}{a_P} \frac{\mathrm{d}P}{\mathrm{d}\tau}=7.5198...\times 10^{3}/\,\sqrt{z}\tag{69}\]
と演算方程式に変換する。電圧換算係数を \(a_P=1/80\)、低速モードの場合の時間換算係数を\(a_{\tau}=10^3\,\)(\(\xi\)0.01mを演算時間10秒に対応させる)とすれば
\[\frac{\mathrm{d}P}{\mathrm{d}\tau}=\frac{1}{40}\sqrt{\frac{2\pi}{z}}=0.06266.../\sqrt{z}\tag{70}\]
となる。
各原変数の値域と、おおまかな関係を図2.3にまとめた。
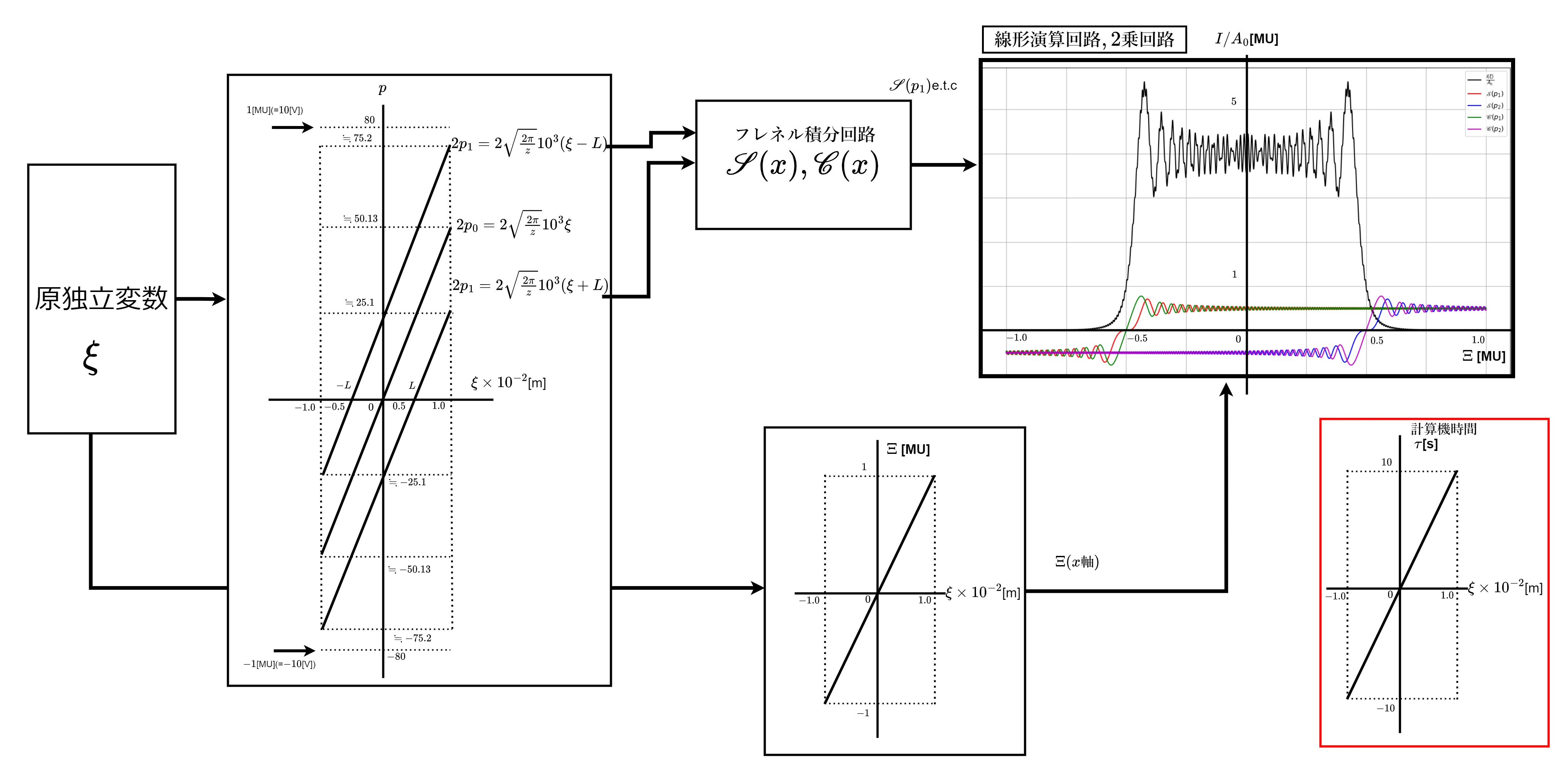
図2.3 変数の値域
さらに、主な原変数と演算変数(計算機変数)の対応関係と、スケーリングの換算係数を表2.1に示す。
表2.1 原変数と演算変数の対応・換算係数(z=1mの場合)
| 原変数 | 演算変数 | 換算係数 |
| \(\xi\)[m] | \(\Xi\) | \(a_{\Xi}=10^{2}\) |
| \(p\)(\(2p_1,2p_2,2p_0\)) | \(P\) | \(a_P=\frac{1}{80}\) |
| \(フレネル積分\) | - | \(1\) |
| \(im(虚部)\,,e(実部)\) | \(Im\) | \(\frac{1}{3}\) |
| \(i\) | \(I\) | \(a_{I}=\frac{1}{6}\) |
\(z\)が1以外の場合は、\(a_{P}=\)フレネル積分回路以降では、虚部が1を超えるので、1以下の換算係数が必要。回折光強度への影響はほぼ虚部によるものと言ってよいだろう。
(変数のスケーリングについては、演算の理論のページを参照されたい。)
定数を積分して\(2P_1,2P_2\)を生成し、フレネル積分ブロックに入力。その出力を線形演算して実部と虚部を生成→2乗→加算の後出力として\(I(\Xi)/A_0\)が得られる。
一方、フレネル積分ブロックの内部は少し工夫を要する。
フレネル積分、たとえば\(\mathscr{S}(p_1^2)\)を得たい場合、その被積分関数\(\sin{(p_2^{2})}\)を先に生成し、それを積分器で積分する。肝心の被積分関数は、以下の連立微分方程式を解く回路により生成している。
\begin{eqnarray} \left\{ \begin{array}{l} \frac{\mathrm{d}}{\mathrm{d}t}\sin(f(t))=\cos(f(t))\frac{\mathrm{d}f(x)}{\mathrm{d}t} \\ \frac{\mathrm{d}}{\mathrm{d}t}\cos(f(t))=-\sin(f(t))\frac{\mathrm{d}f(x)}{\mathrm{d}t}\end{array} \right. \tag{68}\end{eqnarray}
\(p_1^2,p_2^2\)そのものではなく\(2p_1,2p_2\)を渡しているのも、この回路が微分値\(\mathrm{d}f(t)/\mathrm{d}t\)を入力として必要とするからである。独立変数に関する微分が用意できる変数は、それをアナログコンピュータ上の積分変数とすることができる。つまり、本来は時間に関する微積分しかできないアナログコンピュータでも、従属変数に関する積分が可能になるのだ。このトリックは非常に便利なのでよく使われる。(特に微分値として可変定数もしくは変数として\(\omega\)を入力し、周波数可変正弦関数・余弦関数回路として用いる用途が多い。)
フレネル積分の被積分関数を積分する4つの積分器は、非零の初期条件を設定しなくてはならない。その初期条件は\(z\)の値に応じて異なり、さらに中途半端な数字であるため、設定には慎重を要する。
3. 結果
3.1 アナログコンピュータによる解析結果
3.1.1 フレネル積分
まずは、正規化していないフレネル積分\(\mathrm{C}(x)\,,\mathrm{S}(x)\)を演算してみる。低速モードでXYレコーダにグラフを描かせた。
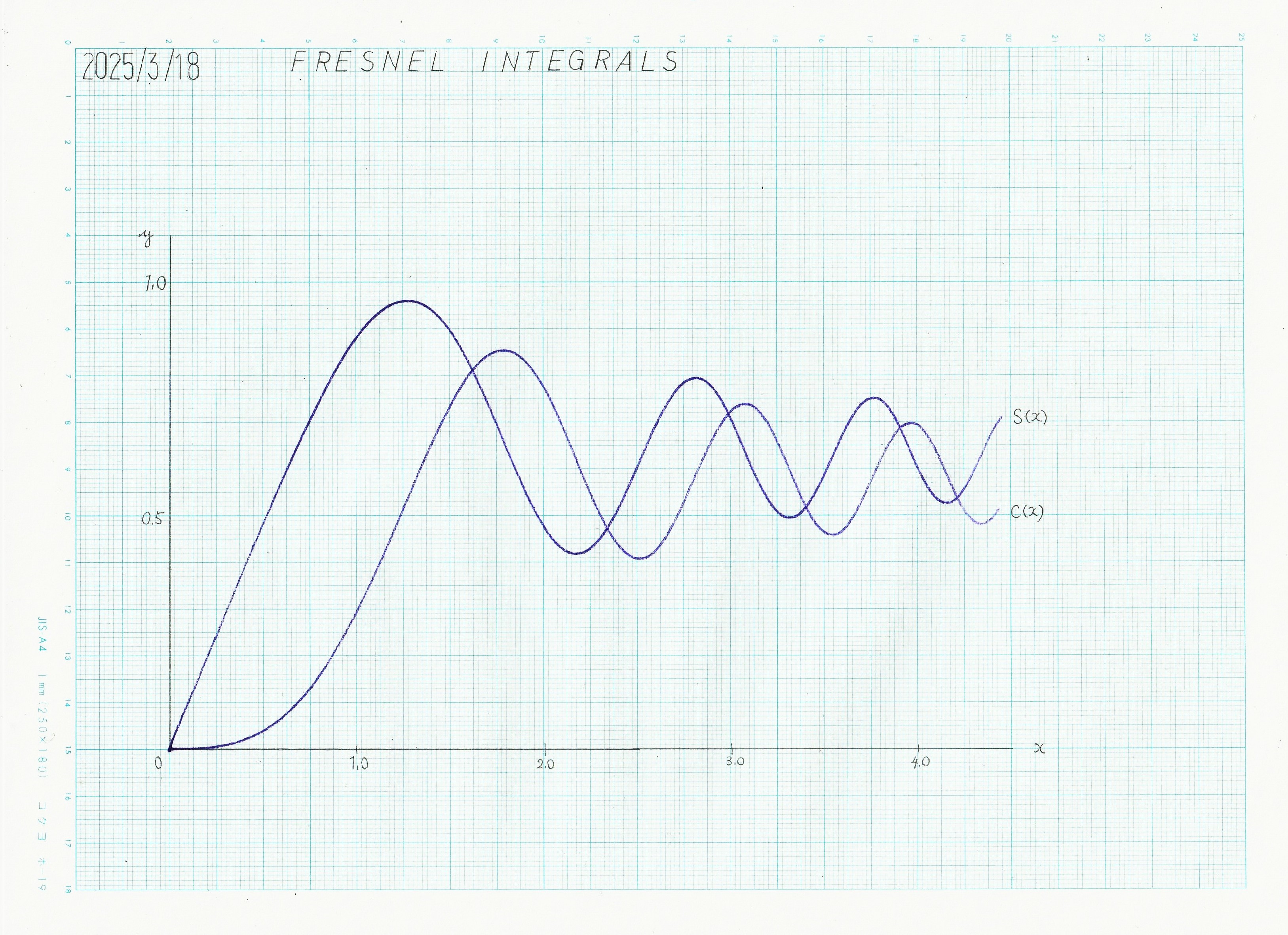
図3.1 フレネル積分のグラフ\(\;(x\leq{0})\)
精度の良い結果が得られた。
3.1.2 無限長スリット
結論から申し上げますと失敗しました。(2025/3/7)
結果:
フレネル積分を生成する開ループ積分器による定積分計算に大きな誤差が生じる。
考えられる原因:
設定する初期条件の僅かな誤差が積分に影響するため。被積分関数 \(\sin{(p^2)}\,,\cos{(p^2)}\)を\(p\)が負から正まで積分する際、\(p\)が0になるタイミングが少しでもズレると積分器出力関数のその後の値が大きく変わってしまう。
やはりアナログ計算機にとって、定積分計算と微分方程式とでは難しさが格段に違う…
3.2 数値計算の結果
python上の数値計算ライブラリ「scipy」の特殊関数モジュール「scipy.special」にはフレネル関数を計算する関数があるので、それを利用して無限長スリットの場合の回折光強度をグラフ化した結果を示す。
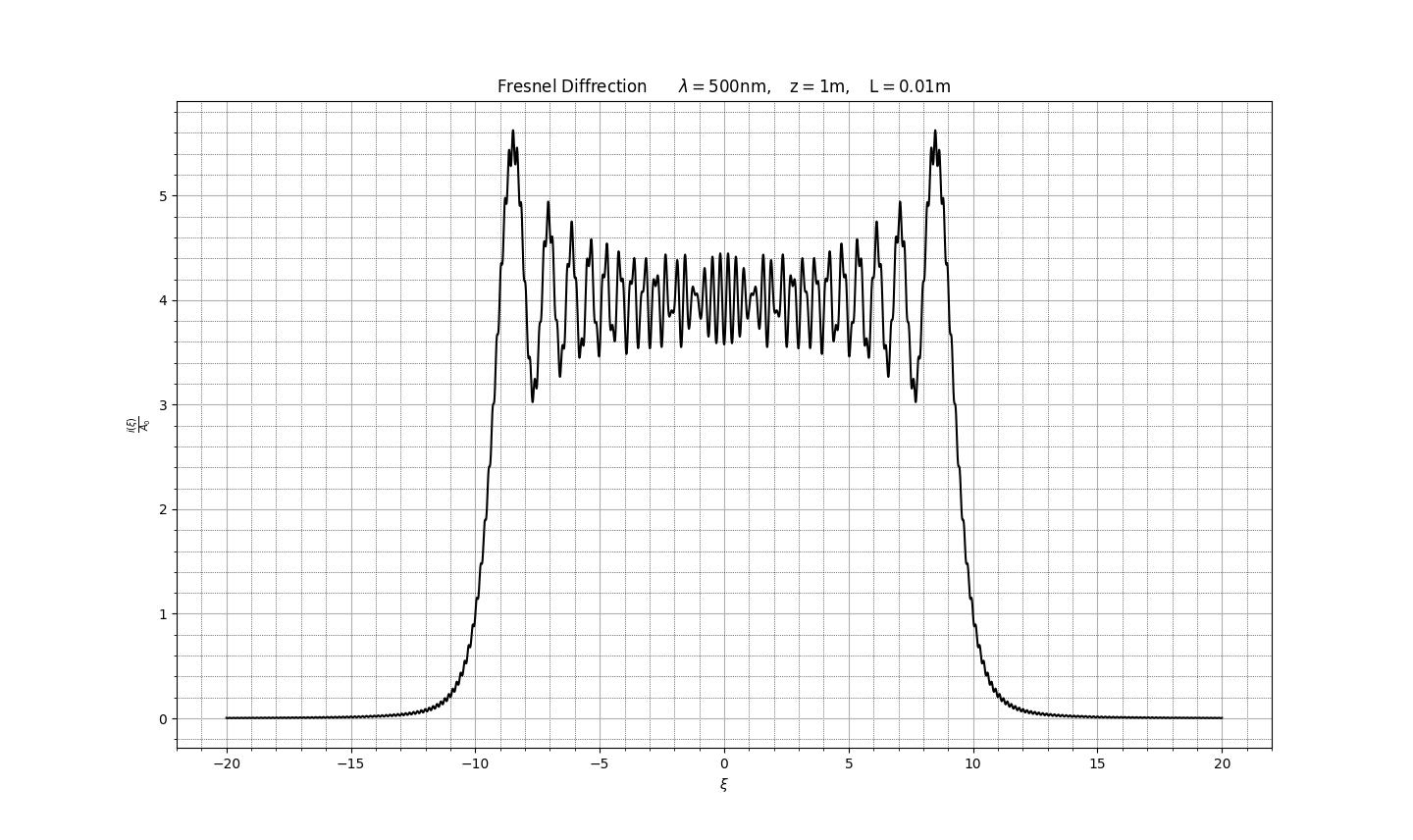
図 3.3 数値シミュレーションの結果
4.参考文献
[1] 大越孝敬. 「光エレクトロニクス」 第1版, 電気通信学会, 1982.
[2] 後藤 憲一, 山崎 修一郎. 「電磁気学演習」 第1版, 共立出版株式会社, 1977.
[3] 村田和美. 「光学」第1版, サイエンス社, 1988.
[4] 工藤恵栄, 上原富美哉 「基礎光学 <光線光学・電磁光学>」第1版, 現代工学社, 1990.
[5] Max Born, Emil Wolf (草川徹 訳)「光学の原理Ⅱ」第7版, 東海大学出版会, 2006.
[6] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」,第1版, 岩波書店, 1975.