表皮効果の導出
目次
円筒導体に高周波電流を流すと、誘導される渦電流により導体中心部の電流が打ち消され、電流密度分布は外周部から中心部にかけて指数関数的に減衰する(表皮効果)。
1.ベッセルの微分方程式
1.1 電流密度の式
円筒導体(断面半径\(r_0\))の軸方向に交番電界\(\boldsymbol{E}\rm{[V/m]}\)が印加され、電流密度\(\boldsymbol{J}\rm[A/m^2]\)の交流電流が流れているとする。電流が比較的低周波で変位電流が無視できる準定常電流の場合、マクスウェル方程式及びオームの法則より、電流密度分布及び電界分布は以下の式で表される。
\[\nabla^2\boldsymbol{J} = \sigma\mu \frac{\partial \boldsymbol{J}}{\partial t}\tag{1}\]
\[\nabla^2\boldsymbol{E} = \sigma\mu \frac{\partial \boldsymbol{E}}{\partial t}\tag{2}\]
なお、\(\sigma\)は導体の導電率、\(\mu\)は導体の透磁率である。
3次元のデカルト座標\((x,y,z)\)を円筒座標系(円柱座標系)\((r,\theta,z)\)に変換する。\(r\)は円柱軸からの距離、\(\theta\)は円柱軸まわりの偏角、\(z\)は円柱基準面からの高さである。
図1.1
\(\boldsymbol{e_r},\boldsymbol{e_\theta},\boldsymbol{e_z}\)を円筒座標系の基底ベクトルとする。
電流密度は\(z\)方向にのみ大きさを持ち、その大きさは\(\theta,z\)に依らないので
\[(\boldsymbol{J_r},\boldsymbol{J_\theta},\boldsymbol{J_z})=(0,0,J_z(r,t))\tag{3}\]
電界についても同様に
\[(\boldsymbol{E_r},\boldsymbol{E_\theta},\boldsymbol{E_z})=(0,0,E_z(r,t))\tag{4}\]
と表せる。(2)式は
\[\frac{1}{r}\frac{\partial}{\partial{r}}\left(r\frac{\partial{\boldsymbol{E}(z,t)}}{\partial{r}}\right) =\sigma\mu \frac{\partial{E_z(r,t)}}{\partial{t}}\]
すなわち
\[\frac{\partial^2E_z(r,t)}{\partial{r^2}}+\frac{1}{r}\frac{\partial{E_z(r,t)}}{\partial{r}}=\sigma\mu \frac{\partial{E_z(r,t)}}{\partial{t}}\tag{5}\]
となる。
一方、円筒導体における電場の回転は
\begin{align*}
\nabla\times\boldsymbol{E}&=\left(\frac{1}{r}\frac{\partial E_z}{\partial\theta}-\frac{\partial E_\theta}{\partial z}\right)\boldsymbol{e_r}+\left(\frac{\partial E_r}{\partial z}-\frac{\partial E_z}{\partial r}\right)\boldsymbol{e_\theta}+\frac{1}{r}\left\{\frac{\partial}{\partial r}\left(rE_\theta\right)-\frac{\partial E_r}{\partial \theta}\right\}\boldsymbol{e_z}\\\\
&=-\frac{\partial E_z\left(r,\ t\right)}{\partial r}\boldsymbol{e_\theta}
\tag{6}\end{align*}
となり、\(\theta\)成分のみ持つことがわかる。となると、ファラデー・マクスウェル方程式
\begin{eqnarray}\nabla\times\boldsymbol{E}\left(x,t\right)=-\mu\displaystyle{\frac{\partial\boldsymbol{H}\left(x,t\right)}{\partial t}}\tag{7}\end{eqnarray}
は次のように書き直せる。
\[\frac{\partial E_z\left(r,\ t\right)}{\partial r}=\mu\frac{\partial H_\theta\left(r,\ t\right)}{\partial t}\tag{8}\]
この式から、電場の回転、すなわち磁束密度(および磁界\(\boldsymbol{H}\))は\(\theta\)成分のみが時間変化することがわかる。
いま、\(E_z(r,t)=E_z(r)e^{j\omega t}, J_z(r,t)=J_z(r)e^{j\omega t}\)と表される交流であるとし、これを(5)式へ代入すれば
\begin{align*}
\frac{\partial^2 E_z\left(r\right)}{\partial r^2}e^{j\omega t}+\frac{1}{r}\frac{\partial E_z\left(r\right)}{\partial r}e^{j\omega t}&=j\sigma\mu\omega E_z\left(r\right)e^{j\omega t}\\\\
\therefore\frac{\mathrm{d}^2 E_z\left(r\right)}{\mathrm{d}r^2}+\frac{1}{r}\frac{\mathrm{d} E_z\left(r\right)}{\mathrm{d}r}-j\sigma\mu\omega E_z\left(r\right)&=0\tag{9}
\end{align*}
\(\sqrt{-j\sigma\mu\omega}=k\quad\rm{[m^{-1}]}\)(\(k\):複素伝搬定数)とおく。
\[\frac{\mathrm{d}^2 E_z\left(r\right)}{\mathrm{d}r^2}+\frac{1}{r}\frac{\mathrm{d} E_z\left(r\right)}{\mathrm{d}r}+k^2 E_z\left(r\right)\tag{10}\]
\(\xi\equiv kr\)(\(\xi\)は無次元変数)なる変換を施すと、
\begin{eqnarray}\mathrm{d}\xi&=&k\mathrm{d}r\\\\ \therefore\frac{1}{\mathrm{d}r}&=&\frac{k}{\mathrm{d}\xi}\tag{11}\end{eqnarray}
より、
\begin{eqnarray}
k^2\frac{\mathrm{d}^2 E_z\left(\xi\right)}{\mathrm{d}\xi^2}+\frac{k^2}{\xi}\frac{\mathrm{d} E_z\left(\xi\right)}{\mathrm{d}\xi}+k^2E_z\left(\xi\right)&=&0\\\\
\therefore\frac{\mathrm{d}^2 E_z\left(\xi\right)}{\mathrm{d}\xi^2}+\frac{1}{\xi}\frac{\mathrm{d}E_z\left(\xi\right)}{\mathrm{d}\xi}+E_z\left(\xi\right)&=&0\tag{12}
\end{eqnarray}
となる。これはベッセルの微分方程式
\[\frac{\mathrm{d}^2y}{\mathrm{d}x^2}+\frac{1}{x}\frac{\mathrm{d}y}{\mathrm{d}x}+\left(1-\frac{n^2}{x^2}\right)y=0\tag{13}\]
の\(n=0\)の場合(n次)である。この基本解として、\(x=0\)で正則な解\(J_n\)(第1種ベッセル関数)と、\(x=0\)で正則でない解\(N_n\)(第2種ベッセル関数/ノイマン関数)とがあるが、導体内部の電流密度・電界を考えているので、前者を解として採用する。
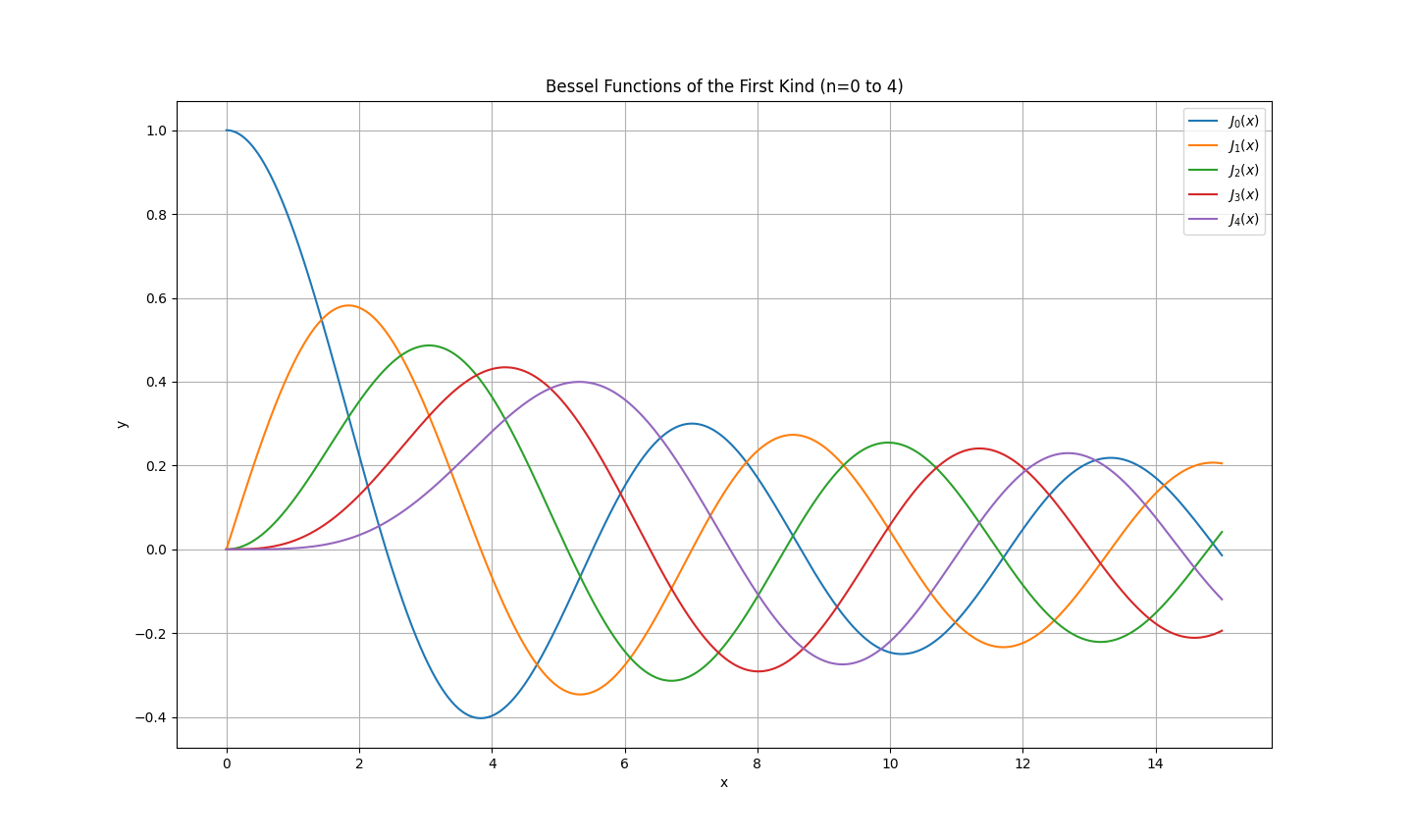
図1.2 第1種ベッセル関数
図1.3 第2種ベッセル関数(ノイマン関数)
\[E_z(r)=AJ_0(\xi)=AJ_0(kr)\tag{14}\]
なお、定係数Aは導体表面における境界条件から決まるものである。
磁界は\(\theta\)成分のみが変化するので、\(\boldsymbol{H}=H_\theta (r,t)e^{j\omega t}\)と表せる。(14)式を(8)式に代入すれば、
\begin{eqnarray}
A\frac{\mathrm{d}}{\mathrm{d}r}J_0\left(kr\right)e^{j\omega t}&=&j\omega\mu H_\theta\left(r\right)e^{j\omega t}\\\\
\therefore A\frac{\mathrm{d}}{\mathrm{d}r}J_0\left(kr\right)&=&j\omega\mu H_\theta\left(r\right)\tag{15}
\end{eqnarray}
第1種ベッセル関数(以後単にベッセル関数と言う)の性質
\[\frac{\mathrm{d}}{\mathrm{d}x}J_0\left(ax\right)=-aJ_1\left(ax\right)\tag{16}\]
から、
\begin{eqnarray}
-AkJ_1\left(kr\right)&=&j\omega\mu H_\theta\left(r\right)\\\\
\therefore H_\theta\left(r\right)&=&j\frac{Ak}{\omega\mu}J_1\left(kr\right)\tag{17}
\end{eqnarray}
となる。
(※式(16)はベッセル関数の級数表示
\[J_n\left(x\right)=\sum^{\infty}_{m=0}\frac{\left(-1\right)^m}{m!\ \Gamma\left(n+m+1\right)}\left(\frac{x}{2}\right)^{n+2m}\tag{17}\]
の項別微分により導かれる。)
ここで、アンペールの法則を用いて導体内の全電流を求めると、
\begin{align*}
I&=\oint\boldsymbol{H}\cdot \mathrm{d}\boldsymbol{s}\\\\
&=\oint H_\theta\left(r_0\right)\cdot r_0\;\mathrm{d}\theta\\\\
&=2\pi r_0 H_\theta\left(r_0\right)\\\\
&=j\frac{2\pi r_0Ak}{\omega\mu}J_1\left(kr_0 \right)\tag{18}
\end{align*}
ゆえに\(A\)は
\begin{align*}
A&=-j\frac{\omega\mu}{2\pi kr_0}\frac{I}{J_1\left(kr_0\right)}\\\\
&=-j\frac{\omega\mu}{2\pi r_0\sqrt{-j\sigma\mu\omega}}\frac{I}{J_1\left(kr_0\right)}\\\\
&=\frac{k}{2\pi r_0\sigma}\frac{I}{J_1\left(kr_0\right)}\tag{19}
\end{align*}
と求まる。したがって、式(14)は
\[E_z\left(r\right)=\frac{kI}{2\pi r_0\sigma}\frac{J_0\left(kr\right)}{J_1\left(kr_0\right)}\tag{20}\]
となり、電流密度は
\[J_z\left(r\right)=\sigma E_z\left(r\right)=\frac{kI}{2\pi r_0}\frac{J_0\left(kr\right)}{J_1\left(kr_0\right)}\tag{21}\]
と表される。
1.2 表皮効果
(9)式において、\(r\)が十分大きいところ(外縁部)の近似解析解をもとめる。1階微分項を無視すると
\[\frac{\mathrm{d}^2 E_z\left(r\right)}{\mathrm{d}r^2}-j\sigma\mu\omega E_z\left(r\right)=0\tag{22}\]
(22)の一般解は
\[E_z(r)=E_0 e^{\sqrt{\frac{\sigma\mu\omega}{2}}(1+j)r}+E_1e^{-\sqrt{\frac{\sigma\mu\omega}{2}}(1+j)r}\tag{23}\]
である。任意定数\(E_0,E_1\)を、実部振幅部が減衰指数関数となる第2項は\(r\rightarrow \infty\)で0に近づき、導体内部の現象にそぐわないので、第1項のみを採用する。つまり
\begin{eqnarray}E_z(r)&=&E_0 e^{\sqrt{\frac{\sigma\mu\omega}{2}}(1+j)r}\\\\&=&E_0 e^{\sqrt{\frac{\sigma\mu\omega}{2}}r}e^{j\sqrt{\frac{\sigma\mu\omega}{2}}r}\tag{24}\end{eqnarray}
複素電流密度は
\[J_z(r)=\sigma E_0 e^{\sqrt{\frac{\sigma\mu\omega}{2}}r}e^{j\sqrt{\frac{\sigma\mu\omega}{2}}r}=\sigma E_0 e^{\sqrt{\frac{\sigma\mu\omega}{2}}r}\left\{\cos{\left(\sqrt{\frac{\sigma\mu\omega}{2}}r\right)}+j\sin{\left(\sqrt{\frac{\sigma\mu\omega}{2}}r\right)}\right\}\tag{25}\]
式(25)の絶対値を取ると、
\[|J_z(r)|=\sigma |E_0| e^{\sqrt{\frac{\sigma\mu\omega}{2}}r}\tag{26}\]
(26)から、\(r\)が大きくなる、つまり導体外周部に向かうにつれ電流密度が大きくなることを示している。いま、
\[\delta \equiv \sqrt{\frac{2}{\sigma\mu\omega}}\tag{27} \]
と定義して(26)式を\(\delta\)で表すと
\begin{eqnarray}|J_z(r)|&=&\sigma |E_0| e^{\sqrt{\frac{\sigma\mu\omega}{2}}r}\\&=&\sigma |E_0| e^{\frac{r}{\delta}}\\&=&\sigma |E_0|e^{\frac{r_0}{\delta}} e^{-\frac{r_0-r}{\delta}}\\&=&|J_0| e^{-\frac{r_0-r}{\delta}}\tag{28}\end{eqnarray}
ただし\(|J_0| \equiv \sigma |E_0| e^{\frac{r_0}{\delta}} \)
\(\delta\)を表皮深さといい、「導体外周部から」の距離が\(\delta\)の位置における電流密度が導体表面における値の\(1/e\)になることを示し、導体の表皮効果の大きさの指標となるパラメータである。
(27)式から、導体の透磁率・導電率、電流周波数が大きいほど表皮深さが浅くなる、つまり表皮効果の影響が大きくなることが分かる。
2.参考文献
[1] 森口繁一, 宇田川銈久, 一松信.「岩波全書 数学公式Ⅲ-特殊関数-」,第1版, 岩波書店, 1975.
[2] 後藤 憲一, 山崎 修一郎. 「電磁気学演習」 第1版, 共立出版株式会社, 1977.
[3] 野邑雄吉. 「応用数学 -工学専攻者のための-」第1版, 内田老鶴圃新社, 1981.
[4] https://denki-no-shinzui.com/skin-effect/.
[5] 多谷虎男. 「ベッセル関数と弾性波動論」第1版, 山海堂, 1986.