円制限3体問題
目次
自作アナログコンピュータで円制限3体問題を解き、小天体の軌道を演算するほか、ゼロ速度曲線の描出も試みる。
1.円制限3体問題の運動方程式とヤコビ積分
重力の相互作用を受ける3質点の運動を調べる三体問題は、一般には解析解が得られないことで有名である。アナログ計算機で3体問題を扱った事例はあまり多くはない(たとえば[1][2])。それもそのはずで、万有重力項1つを計算するだけもかなりの非線形演算器が必要となり、コスト・計算精度の問題が生じうる。条件を緩め、第3体天体の質量が他と比べ微小と仮定し、第1、第2天体の軌道も円で近似できると仮定する円制限三体問題としても、例えば直交座標系で扱うなら、1項分は乗算器×2→平方根回路→乗算器×2(3乗)→除算回路という構成となり、乗算器は6個必要となる。系全体で考えると計12個の乗算器が必要になるわけだ。また、途中に除算回路があるのでダイナミックレンジの問題も生じる。アナログ計算の不得意とするところが"増幅"されてしまうわけである。
\[F(r)=-G\,\frac{m_1\,m_2}{r^{3}}\tag{1}\]
(\(F\):天体1と天体2間の万有引力, \(G\):万有引力定数, \(m_1,m_2\):各天体の質量, \(r\):天体間距離)
アナログ計算機による3体問題の解析をメインに扱った論文中でも、デジタル計算機([2]で挙げられているのはIBM650、IBM7090)による数値解析例が正確解として扱われ、アナログ計算機による実験解との比較に利用されている。[2]ではリレーによりアナログ除算のスケーリングを逐次変更することでSN比の改善を試みているようであるが、誤差の完全な補正には至っていない。
私の自作機では現代のアナログIC技術の性能を十分に発揮できるわけであるが、そのような困難にどれくらい太刀打ちできるか非常に興味深い。
2.アナログコンピュータプログラム
2.1 運動方程式とゼロ速度曲線
\(\xi-\eta\)平面上における運動に限定し、質量 \(m_1\) の第1天体の座標を \((\xi_1,\eta_1)\)、質量 \(m_2\) の第2天体の座標を \((\xi_2,\eta_2)\)、微小質量の第3天体の座標を \((\xi, \eta)\) とし、第3天体と第1天体、第2天体との距離をそれぞれ \(r_1\), \(r_2\)とすれば、第3天体の運動方程式は以下のようになる。
\begin{eqnarray}\frac{\mathrm{d}^2\xi}{\mathrm{d}t^2}=-m_1\,G\,\frac{(\xi-\xi_1)}{r_1^3}-m_2\,G\,\frac{(\xi-\xi_2)}{{r_2}^3}\tag{2}\\\\\frac{\mathrm{d}^2\eta}{\mathrm{d}t^2}=-m_1\,G\,\frac{(\eta-\eta_1)}{r_1^3}-m_2\,G\,\frac{(\eta-\eta_2)}{{r_2}^3}\tag{3}\end{eqnarray}
第1天体と第2天体(以後「主天体」と総称)の重心位置に原点を置く回転座標系を考える(図1)。第1天体の座標を \((x_1,y_1)\)、第2天体の座標を \((x_2,y_2)\)、第3天体の座標を \((x, y)\) とすれば、運動方程式を以下のように書き換えることができる。
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=2\omega\frac{\mathrm{d}y}{\mathrm{d}t}+\omega^2\,x-m_1\,G\,\frac{(x-x_1)}{r_1^3}-m_2\,G\,\frac{(x-x_2)}{{r_2}^3}\tag{4}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}t^2}=-2\omega\frac{\mathrm{d}x}{\mathrm{d}t}+\omega^2\,y-m_1\,G\,\frac{(y-y_1)}{r_1^3}-m_2\,G\,\frac{(y-y_1)}{{r_2}^3}\tag{5}\end{eqnarray}
ただし \(\omega\) は座標系の回転角速度。主天体は円軌道であると想定したため、角速度は定数であり、運動方程式は時間依存しない自律系となっている。
簡単のため、各定数を \(\omega=1,\; m_1+m_2=1,\; m_1=\mu,\; m_2=1-\mu,\; G=1\)と単純化する。
図1
運動方程式は
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}&=&2\,\frac{\mathrm{d}y}{\mathrm{d}t}+x-(1-\mu)\,\frac{(x-\mu)}{{r_1}^3}-\mu\,\frac{(x-1+\mu)}{{r_2}^3}\tag{6}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}t^2}&=&-2\,\frac{\mathrm{d}x}{\mathrm{d}t}+\,y-(1-\mu)\,\frac{y}{{r_1}^3}-\mu\,\frac{y}{{r_2}^3}\tag{7}\end{eqnarray}
となる。ただし、
\begin{eqnarray}r_1&=&\sqrt{(x+\mu)^2+y^2}\tag{8}\\\\r_2&=&\sqrt{(1-\mu-x)^2+y^2}\tag{9}\end{eqnarray}
上記連立微分方程式をアナログコンピュータにプログラムし、積分器に適切な初期条件(初期位置・初速度)を与えれば、第3天体の軌道をXYレコーダやオシロスコープ上で表示することができる。
いっぽう、運動方程式(6),(7)の積分(いわゆる第一積分)が計算でき、その積分定数(ヤコビ定数)を \(C\) とすれば、
\[x^2+y^2+2\,\frac{1-\mu}{r_1}+2\,\frac{\mu}{r_2}-{\dot{x}}^2-{\dot{y}}^2=C\tag{10}\]
と表される。これが、系の唯一の保存量「ヤコビ積分」である。相対速度項(1階時間微分項の2乗和)は運動エネルギー、それ以外の変数項は(擬似)有効ポテンシャル \(\Omega(x,y)\) の2倍である。第3天体が前述の運動方程式に従う限り、そしてパラメータが不変である限り、位置と速度が変化してもヤコビ積分の値は初期条件により決まる一定値をとる。また、\(C\)の値が大きい軌道ほど、同じ地点での速度が小さくなることを意味する。
速度項を0としたときのヤコビ積分の表式
\[2\Omega{(x,y)}=x^2+y^2+2\,\frac{1-\mu}{r_1}+2\,\frac{\mu}{r_2}\tag{11}\]
は、x-y座標上でCの値に応じた代数曲線を描く。その曲線をゼロ(相対)速度曲線と呼ぶ[3][4]。
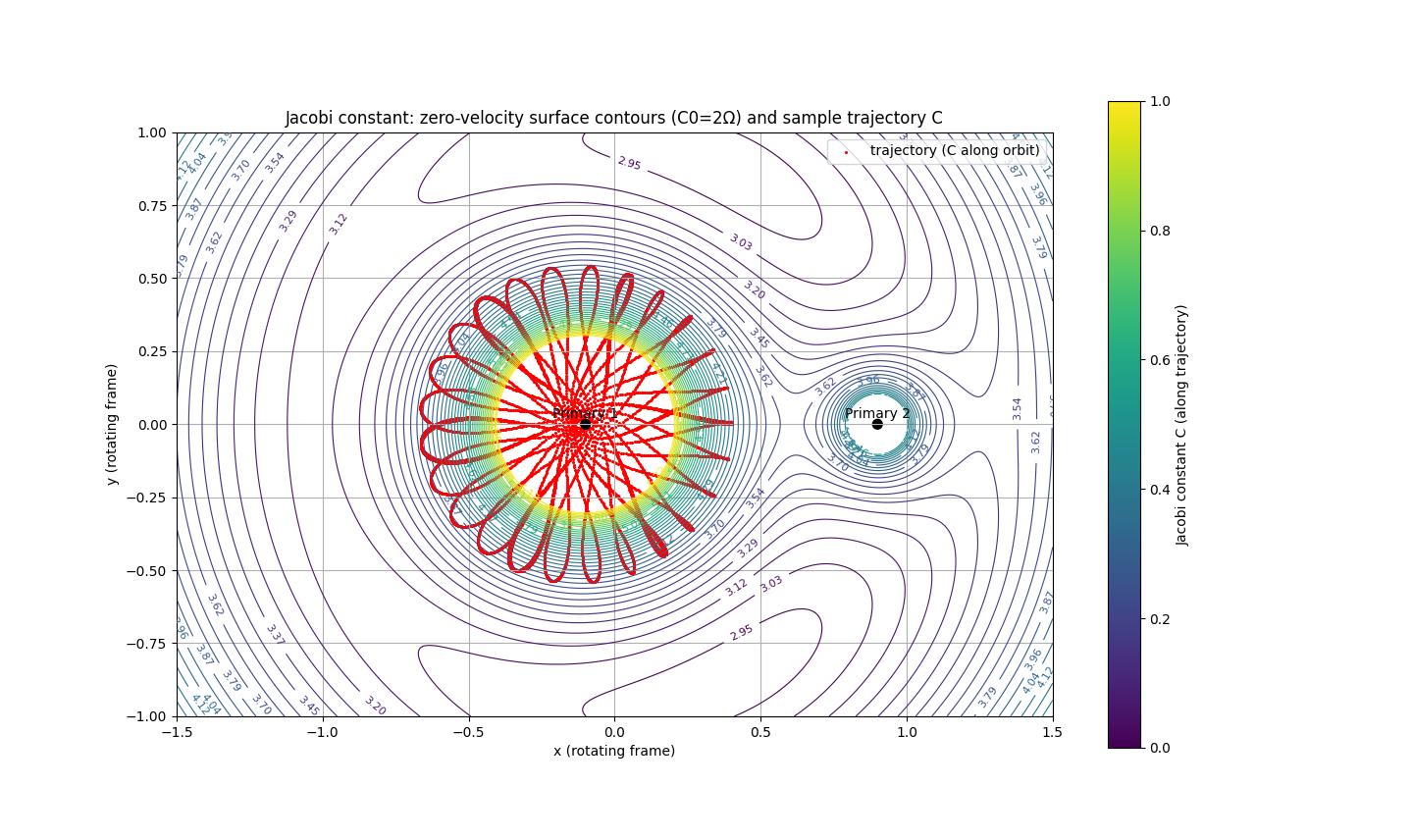
図2 ヤコビ積分の値に応じたゼロ速度曲線の分布と第3天体の軌道例(赤線) 初期条件:\((x,y)=(0.4,0)\) \((v_x,v_y)=(0,0)\)
ゼロ速度曲線により、ある特定のヤコビ積分の値をもつ第3天体が到達可能な領域が決定される。第3天体がそのヤコビ積分に対応するゼロ速度曲線に到達すると速度が0になるため、それより外側に進出できず、その後重力で加速され再び引き戻される。\(C\)の値が大きいと第3天体の軌道は閉じ込められ、小さくなると主天体の重力場から逃れて遠方に飛び出すことが可能となることがわかる。
(5)式で示したポテンシャル \(\Omega(x,y)\) を用いて運動方程式(3)を書き直せば、
\begin{eqnarray}\frac{\mathrm{d}^2x}{\mathrm{d}t^2}-2\,\frac{\mathrm{d}y}{\mathrm{d}t}&=&x-(1-\mu)\,\frac{(x-\mu)}{{r_1}^3}-\mu\,\frac{(x-1+\mu)}{{r_2}^3}=\frac{\partial{\Omega}}{\partial{x}}\tag{12}\\\\\frac{\mathrm{d}^2y}{\mathrm{d}t^2}+2\,\frac{\mathrm{d}x}{\mathrm{d}t}&=&y-(1-\mu)\,\frac{y}{{r_1}^3}-\mu\,\frac{y}{{r_2}^3}=\frac{\partial{\Omega}}{\partial{y}}\tag{13}\end{eqnarray}
である。ゼロ速度曲線の図からもわかるように、本系は5つの(数学的な意味での)平衡点が存在し、それぞれ \(L_1\)~\(L_5\) と名付けられている。それらはすなわち、位置の時間1階微分及び時間2階微分を0とする点であり、関数\(\Omega\)の勾配が0となる点である。 \(L_1\)~\(L_3\) はx軸上に存在する鞍点(不安定平衡点)であり、共線点(オイラーの平衡点)という。\(L_4\)、\(L_5\)は質量比によって安定/不安定が異なる三角点(ラグランジュの平衡点)であり、主天体と正三角形を形づくる。安定な場合は中心点となる(すなわち平衡点近傍における振動的解が許される)。いっぽう、不安定な場合は鞍点に分類される。
これら5平衡点は3体問題の特別解(共線点に留まる解、三角点に留まる解)を与える点であり、その観点から秤動点とも呼称される。
2.2 ゼロ速度曲線の最急降下法を用いた描画
ゼロ速度曲線(ヤコビ積分=Cを満たす曲線)をx-y平面上で描画したいとき、陰伏代数方程式
\begin{eqnarray}f{(x,y)}&=&2\Omega-C\\\\&=&x^2+y^2+2\,\frac{1-\mu}{r_1}+2\,\frac{\mu}{r_2}-C=0\tag{14}\end{eqnarray}
をアナログ計算機で解けばよい。多変数の代数方程式をアナログ計算機で解く方法はいくつかあるが、代表的なものは下に示すような1階微分方程式への変換と最急降下法の組み合わせである。
ゼロ速度曲線上では、すべての時刻において上記 \(f(x,y)\) が不変であるためには、時間全微分\(\mathrm{d}f/\mathrm{d}t\) が恒等的に0でなくてはならない。すなわち
\[\frac{\mathrm{d}f}{\mathrm{d}t}=\frac{\partial{f}}{\partial{x}}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial{f}}{\partial{y}}\frac{\mathrm{d}y}{\mathrm{d}t}=0\tag{15}\]
が常に満たされる必要がある。上式を成立させる十分条件として
\begin{eqnarray}\frac{\mathrm{d}x}{\mathrm{d}t}=\pm\,k_1\,\frac{\partial{f}}{\partial{y}}\tag{16}\\\\\frac{\mathrm{d}y}{\mathrm{d}t}=\mp\,k_2\,\frac{\partial{f}}{\partial{x}}\tag{17}\end{eqnarray}
なる式を選び、演算回路を組めば、その解はx-y平面上で特定のCの値のゼロ速度曲線をえがく。(任意定数 \(k_1,k_2\gt{0}\))上式は、\(C(x,y)=\rm{const.}\) の接ベクトルを時間積分することで平面上に等高線を描く微分方程式である。右辺の正負符号の組み合わせは、軌道を進む向きに影響し、定数 \(k_1\)、\(k_2\)の大きさは、軌道を進む速さに影響するものである。
この手法で原理的には正確な解を得られるはずだが、実際には演算器の静的・動的誤差で別の軌道(異なるヤコビ積分値のゼロ速度曲線)に遷移してしまうことが多々ある。その防止策としては、評価関数として系のエネルギー積分(本問題における\(f\) )の2乗もしくは絶対値として選んだ最急降下法(最急勾配法)により同一軌道を強制的に維持・吸着させる手法が有効である。仮に \({f(x,y)}^2\)を評価関数 \(\varepsilon(x,y)\) として選んだ場合、\(f(x,y)=0\) を自動的に満足せしめるための最急降下軌道の方程式は、正定数 \(k_3,k_4\) を用いて表せば次のようになる。
\begin{eqnarray}\frac{\mathrm{d}x}{\mathrm{d}t}=-k_3\,\frac{\partial{\varepsilon}}{\partial{x}}=-2\,k_3\,f\,\frac{\partial{f}}{\partial{x}}\tag{18}\\\\\frac{\mathrm{d}y}{\mathrm{d}t}=-k_4\,\frac{\partial{\varepsilon}}{\partial{x}}=-2\,k_4\,f\,\frac{\partial{f}}{\partial{y}}\tag{19}\end{eqnarray}
(16)~(19)を組み合わせると
\begin{eqnarray}\frac{\mathrm{d}x}{\mathrm{d}t}=\pm\,k_1\,\frac{\partial{f}}{\partial{y}}-2\,k_3\,f\,\frac{\partial{f}}{\partial{x}}\tag{20}\\\\\frac{\mathrm{d}y}{\mathrm{d}t}=\mp\,k_2\,\frac{\partial{f}}{\partial{x}}-2\,k_4\,f\,\frac{\partial{f}}{\partial{y}}\tag{21}\end{eqnarray}
(18),(19)を原方程式とすれば、(14),(15)式を実装するよりも高精度な曲線追跡が可能になる。
2.3 スケーリング・演算方程式
以降、位置変数に対する換算係数を \(a\) に統一する。すなわち
\[X=a\,x,\;Y=a\,y\tag{22}\]
最初に原方程式 (6),(7)に対してスケーリングを行う。2階微分方程式であるので、速度項のスケールも気にする必要がある。1階微分項の換算係数を\(b\) とし、時間換算係数を無視すると
\begin{eqnarray}\frac{\mathrm{d}^2X}{\mathrm{d}\tau^2}&=&\frac{2}{b}\,\frac{\mathrm{d}Y}{\mathrm{d}\tau}+\frac{X}{a}-(1-\mu)\,\frac{X/a-\mu}{{\sqrt{\left(\frac{X}{a}+\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}-\mu\,\frac{X/a-(1-\mu)}{{\sqrt{\left(\frac{X}{a}-1+\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}\\\\&=&\frac{2}{b}\,\frac{\mathrm{d}Y}{\mathrm{d}\tau}+\frac{X}{a}-a^2\,\left[(1-\mu)\,\frac{X-a\mu}{{\sqrt{\left(X+a\mu\right)^2+Y^2}\,}^3}+\mu\,\frac{X-a(1-\mu)}{{\sqrt{\left\{X-a(1+\mu)\right\}^2+Y^2}\,}^3}\right]\tag{23}\\\\\frac{\mathrm{d}^2Y}{\mathrm{d}\tau^2}&=&-\frac{2}{b}\,\frac{\mathrm{d}X}{\mathrm{d}\tau}+\,\frac{Y}{a}-(1-\mu)\,\frac{Y/a}{{\sqrt{\left(\frac{X}{a}+\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}-\mu\,\frac{Y/a}{{\sqrt{\left(\frac{X}{a}-1+\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}\\\\&=&-\frac{2}{b}\,\frac{\mathrm{d}X}{\mathrm{d}\tau}+\,\frac{Y}{a}-a^2\,\left[(1-\mu)\,\frac{Y}{{\sqrt{\left(X+a\,\mu\right)^2+Y^2}\,}^3}+\mu\,\frac{Y}{{\sqrt{\left\{X-a\,(1-\mu)\right\}^2+Y^2}\,}^3}\right]\tag{24}\end{eqnarray}
次に、原方程式 (18),(19)に対してスケーリングを行う。1階微分方程式であるので、今回は速度項のスケールを気にする必要はないが、偏微分項の連鎖律による数学的スケーリング則
\[\frac{\partial}{\partial{x}}F(X,Y)=\frac{\partial}{\partial{x}}{f\left(\frac{X}{a},\frac{Y}{a}\right)}=\frac{\partial}{\partial{X}}{f\left(\frac{X}{a},\frac{Y}{a}\right)}\cdot\frac{\partial{X}}{\partial{x}}=\frac{\partial{f}}{\partial{x}}\cdot{\frac{1}{a}}\tag{25}\]
に注意せよ。\(f\) の1階空間微分
\[\frac{\partial{f}}{\partial{x}}=2\left\{x-(1-\mu)\,\frac{x+\mu}{{\sqrt{(x+\mu)^2+y^2}}\,^3}-\mu\,\frac{x-1+\mu}{{\sqrt{(x-1+\mu)^2+y^2}}\,^3}\right\}\tag{26}\]
\[\frac{\partial{f}}{\partial{y}}=2\left\{y-(1-\mu)\,\frac{y}{{\sqrt{(x+\mu)^2+y^2}}\,^3}-\mu\,\frac{y}{{\sqrt{(x-1-\mu)^2+y^2}}\,^3}\right\}\tag{27}\]
を \(x,y\) についてスケーリングすると、
\begin{eqnarray}\frac{\partial{F}}{\partial{X}}&=&2\,a\,\left\{\frac{X}{a}-(1-\mu)\,\frac{\frac{X}{a}+\mu}{{\sqrt{\left(\frac{X}{a}+\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}-\mu\,\frac{\frac{X}{a}-1+\mu}{{\sqrt{\left(1-\mu-\frac{X}{a}\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}\right\}\\\\&=&{2X}-2a^3\,\left[(1-\mu)\,\frac{X+a\mu}{{\sqrt{\left(X+a\mu\right)^2+Y^2}\,}^3}+\mu\,\frac{X-a(1-\mu)}{{\sqrt{\left\{X-a(1-\mu)\right\}^2+Y^2}\,}^3}\right]\tag{28}\end{eqnarray}
\begin{eqnarray}\frac{\partial{F}}{\partial{Y}}&=&2\,a\,\left\{\frac{Y}{a}-(1-\mu)\,\frac{\frac{Y}{a}}{{\sqrt{\left(\frac{X}{a}+\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}-\mu\,\frac{\frac{Y}{a}}{{\sqrt{\left(\frac{X}{a}-1-\mu\right)^2+\left(\frac{Y}{a}\right)^2}\,}^3}\right\}\\\\&=&{2Y}-2a^3\,\left[(1-\mu)\,\frac{Y}{{\sqrt{\left(X+a\mu\right)^2+Y^2}\,}^3}+\mu\,\frac{Y}{{\sqrt{\left\{X-a(1-\mu)\right\}^2+Y^2}\,}^3}\right]\tag{29}\end{eqnarray}
となる。
\(f\) 自体を \(x,y\) についてスケーリングすると、
\begin{eqnarray}F(X,Y)&=&\left(\frac{X}{a}\right)^2+\left(\frac{Y}{a}\right)^2+\frac{2(1-\mu)}{\sqrt{\left(\frac{X}{a}+\mu\right)^2+\left(\frac{Y}{a}\right)^2}}+\frac{2\mu}{\sqrt{\left(\frac{X}{a}-1-\mu\right)^2+\left(\frac{Y}{a}\right)^2}}-C\\\\&=&\left(\frac{X}{a}\right)^2+\left(\frac{Y}{a}\right)^2+2a\,\left[\frac{1-\mu}{\sqrt{\left(X+a\mu\right)^2+Y^2}}+\frac{\mu}{\sqrt{\left\{X-a(1-\mu)\right\}^2+Y^2}}\right]-C\tag{30}\end{eqnarray}
と表される。
ほかに、時間微分についての連鎖律による数学的スケーリング則
\[\frac{\mathrm{d}X}{\mathrm{d}t}=a\cdot\,\frac{\mathrm{d}x}{\mathrm{d}t}\,,\quad\,\frac{\mathrm{d}Y}{\mathrm{d}t}=a\cdot\,\frac{\mathrm{d}y}{\mathrm{d}t}\tag{31}\]
を考えることもできるが、どうせ方程式右辺に等しく \(a\) がかかるだけで、描かれる軌道に変化に全く影響がなく、気にしなくてよい。つまり、(31)は時間換算係数として取り扱うのがよく、そもそも電圧換算(振幅換算)には無関係である。
\(F\) の換算係数 \(a_{F}\)、1階空間微分項自体の換算係数 \(a_{\partial}\)も加味した場合の演算方程式を書き表すと以下のようになる。
\begin{eqnarray}\frac{\mathrm{d}X}{\mathrm{d}\tau}=\pm\,\frac{a\,k_1}{a_{\partial}}\,\frac{\partial{F}}{\partial{Y}}-2\,\frac{a\,k_3}{a_{\partial}a_{F}}\,F\,\frac{\partial{F}}{\partial{X}}\tag{32}\\\\\frac{\mathrm{d}Y}{\mathrm{d}\tau}=\mp\,\frac{a\,k_2}{a_{\partial}}\,\frac{\partial{F}}{\partial{X}}-2\,\frac{a\,k_4}{a_{\partial}a_{F}}\,F\,\frac{\partial{F}}{\partial{Y}}\tag{33}\end{eqnarray}
以上の他に、スケーリングが必要な箇所は適宜スケールダウンすること(加算器出力や除算器出力などは特に注意)。除算器については、分子入力をフルスケールの1/10程度に抑えることを目安にする。
\(mu=0.1\) の場合、ゼロ速度曲線の描画で2次元平面状に信号飽和の恐れのある変数の等高線等をプロットし、スケーリングの補助とすると良い。概算に基づく大雑把な図を手描きするだけでよいのだが、デジタルコンピュータにより計算したより正確なプロット例を示すと以下のようになる。(ただし、\(r_1,r_2\)などは位置変数についてのスケール後の値で、\(a=2/3\) )
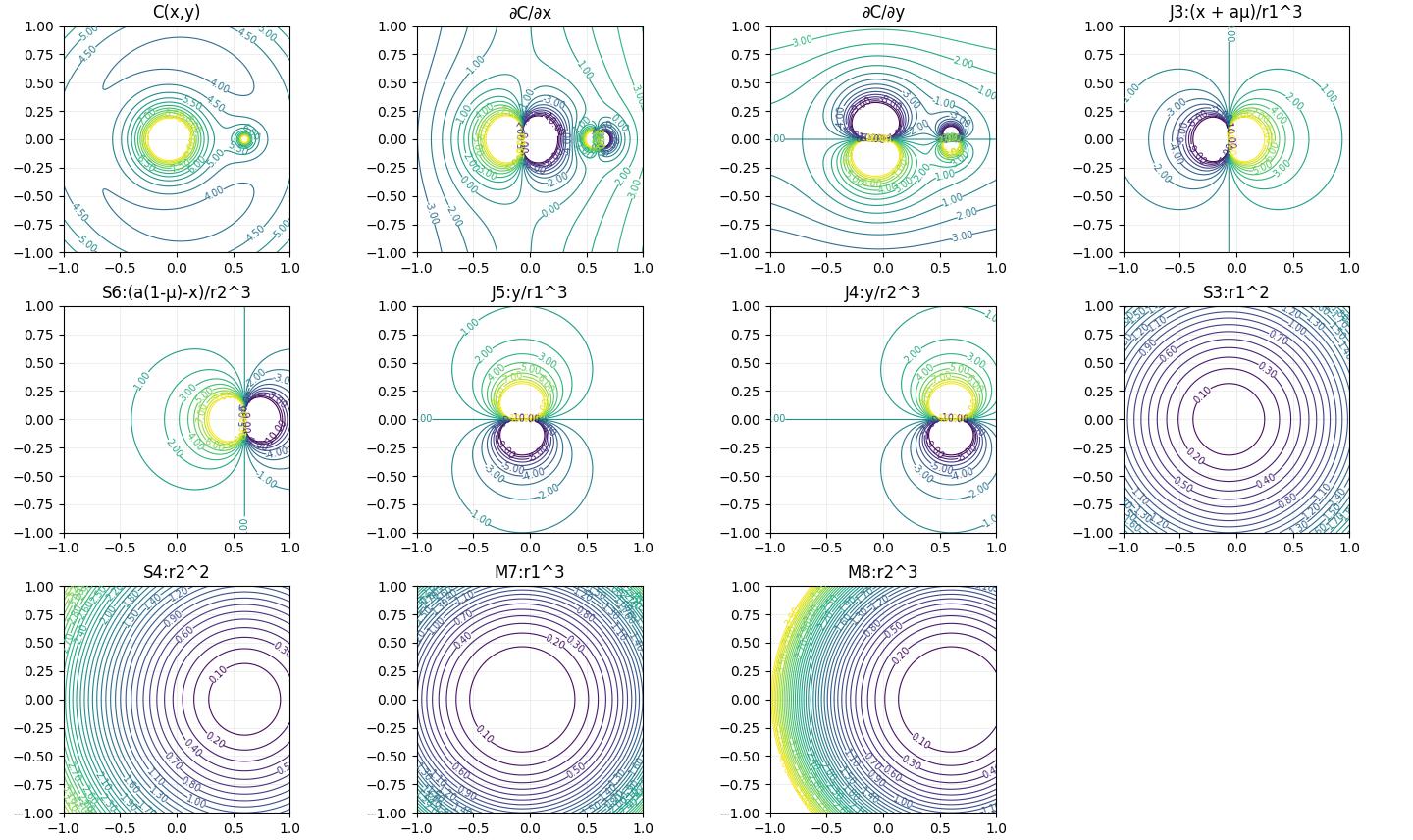
図3 各変数のコンタープロット
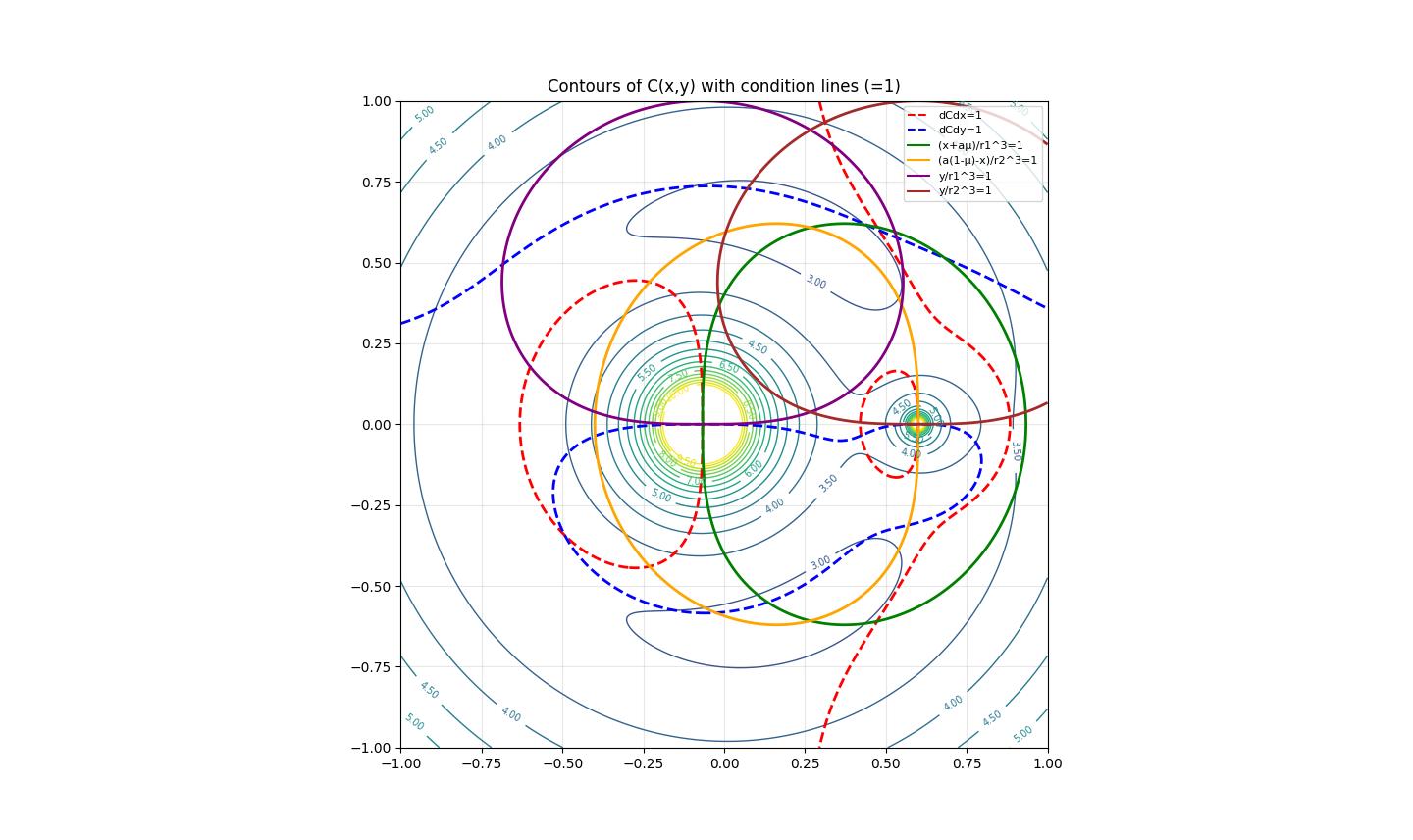
図4 飽和限界
上の図における位置 1.0 が 原変数の1.5 に相当することに注意。上記範囲で各演算変数が1.0を超えないように回路を工夫する。
ゲインの不均衡・過不足を生み出す結線ミスは、相平面上の速度ベクトルの不均衡を生み出し、結果としてあるはずのない「湧き出し・吸い込み」を発生させることがある。保存系なので系の発散は至る所で0のはずである。おかしな現象が生じたら、計算機の故障を疑う前に、プログラムをもう1度見直したり、デジタルシミュレーションの結果と比較したりすることをお勧めする。(私は結線ミス以前に、式のスケーリングの間違いに気づかず数日を無駄にした。(28)式右辺第3項の符号を誤って逆転させると、L4が沈点、L5は源点になる。)
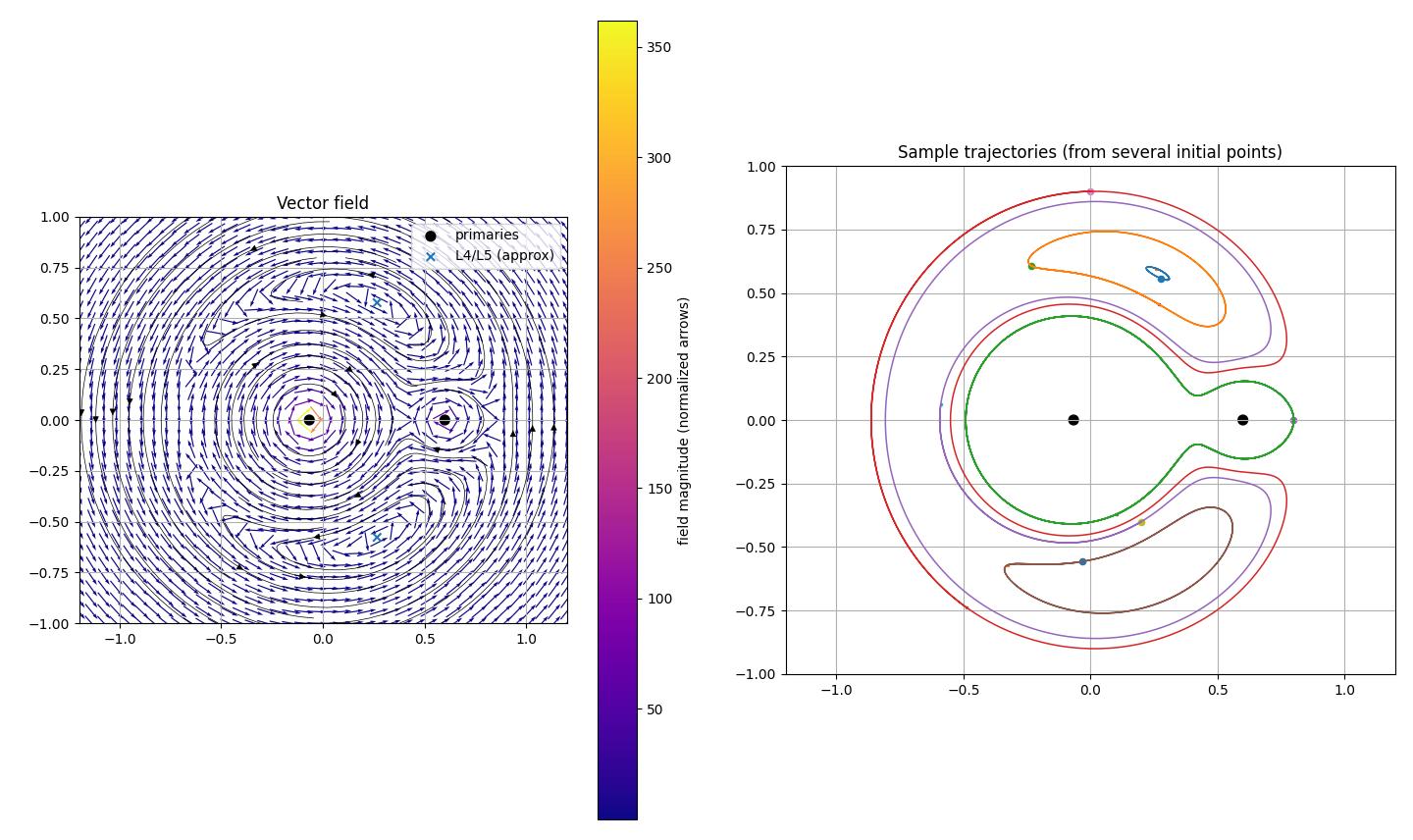
図5 ベクトル図と等高線微分方程式の軌道解析解(発散が0か視覚的に確認)
2.4 演算回路
取り敢えず \(\mu=0.1\) とし、各換算係数を、\(a=2/3\)、\(b=0.25\)、\(a_{F}=a_{\partial}=0.2\) と定める。
2.4.1 運動方程式の演算回路
図6 運動方程式の演算回路
2.4.2 ヤコビ積分の等高線の演算回路
図7 ヤコビ積分の等高線の演算回路
3.結果
第3天体の軌道プロットとヤコビ積分の等高線両方の演算結果を示す。
図8 第3天体の軌道演算例
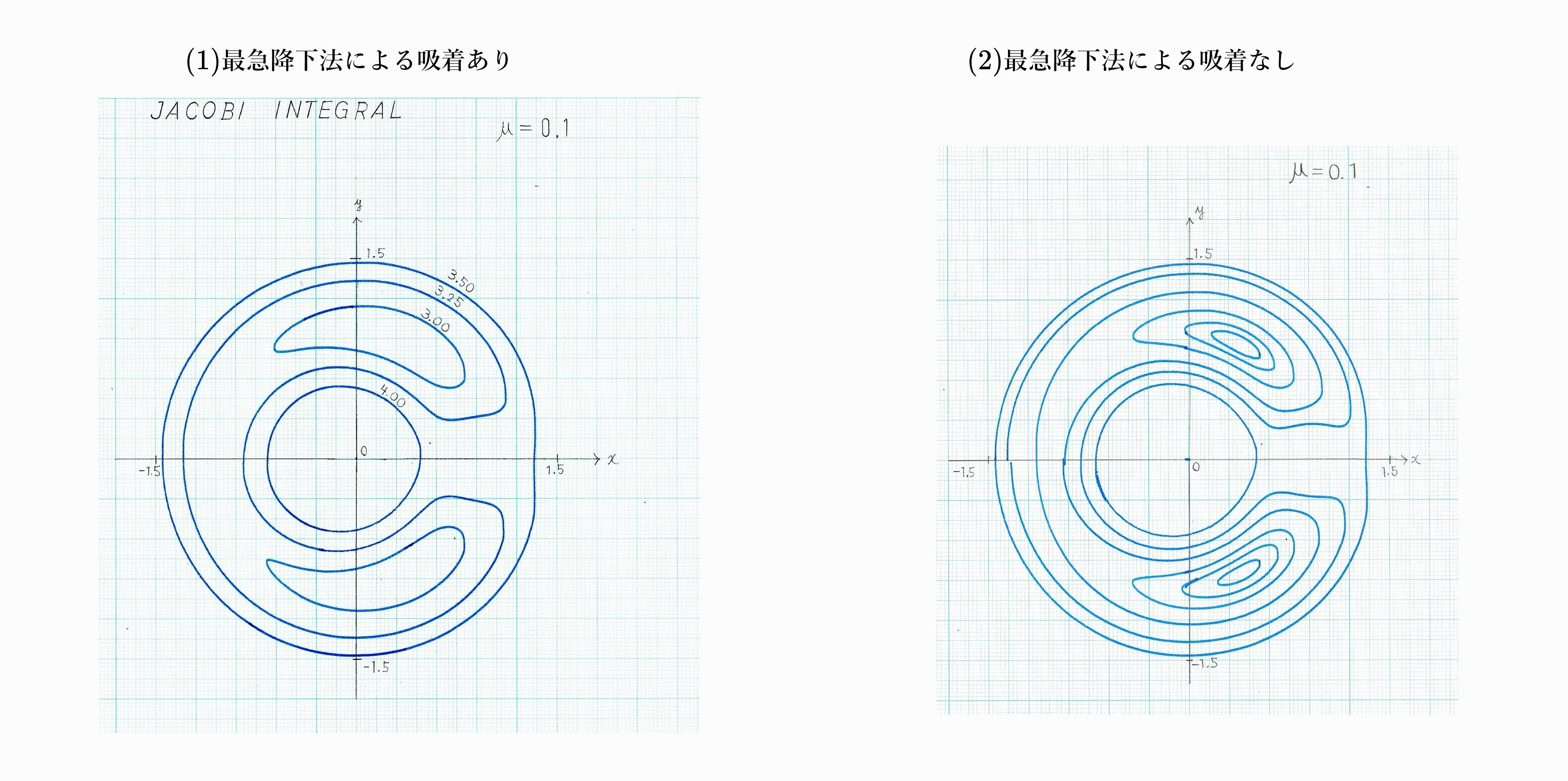
図9 ヤコビ積分の等高線図
4.参考文献
[1] Bernd Ulman. "Celestial mechanics: Three-body problem," https://anabrid.com/media/pages/publikation-dateien-nur-zur-verwaltung-der-dateien/52e5c73333-1745412672/alpaca_11.pdf (2025/8/17 閲覧)
[2] C. J. Sheehan, "An Analog Computer Simulation of the Restricted Three-Body Problem by Automatic Scale-Changing Techniques," in IEEE Transactions on Electronic Computers, vol. EC-13, no. 1, pp. 41-50, 1964.
[3] 萩原 雄祐.「天文学総論 上巻」第1刷, 岩波書店,1955.
[4] 前田 弘. 「スペースクラフトの運動と制御」 計測と制御, 23 巻, 1 号, p. 86-92, 1984. https://www.jstage.jst.go.jp/article/sicejl1962/23/1/23_1_86/_article/-char/ja/