ケプラー方程式
目次
1.ケプラー方程式の導出
離心率\(e\)、短径\(b\)、長径\(a\)の楕円軌道上を周期\(T\)で公転する惑星(点P)を考える(図1.1)。
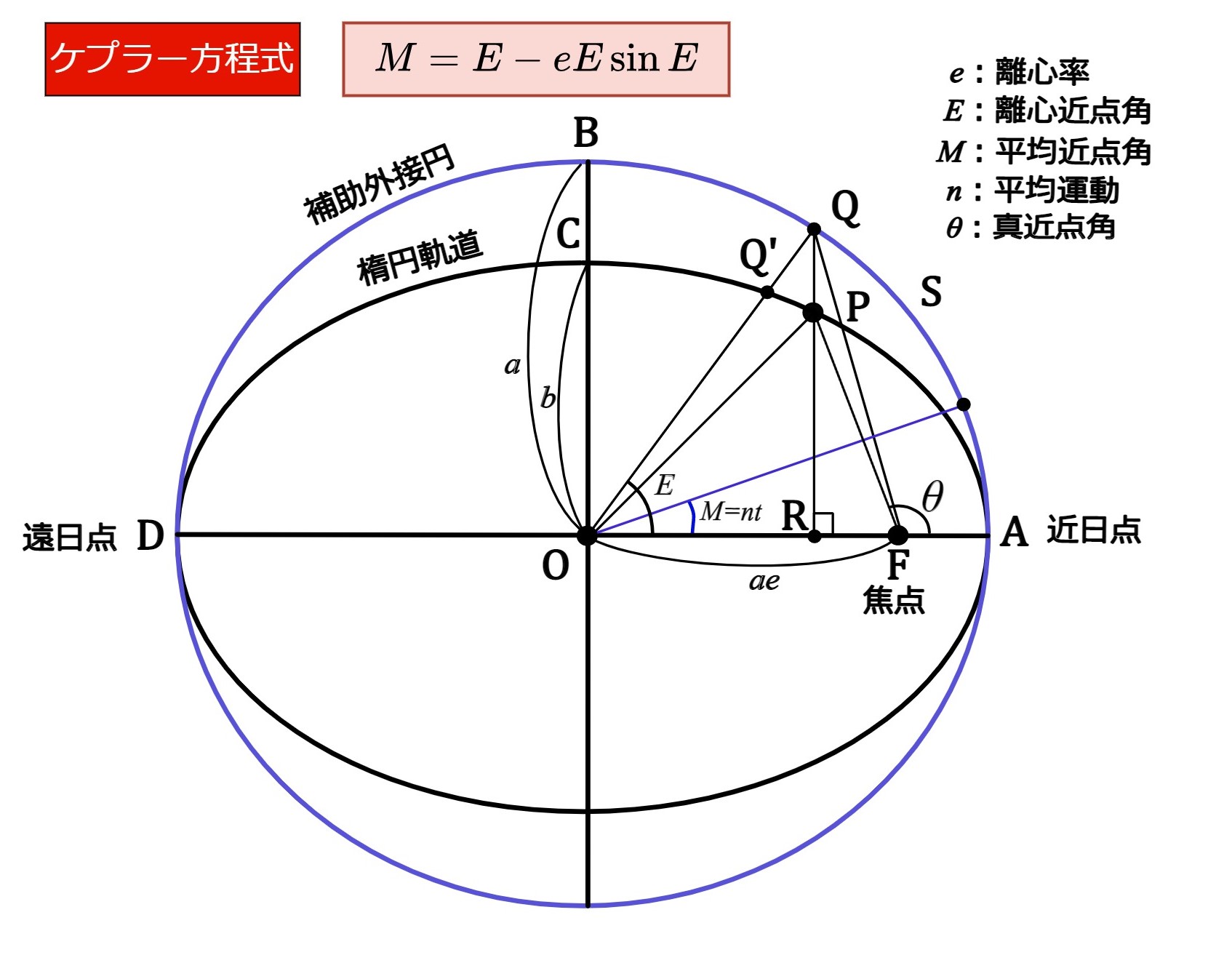
図1 惑星の軌道
Aが近日点、Dが遠日点であり、Fは楕円軌道の焦点である。
円軌道上のP点から楕円長軸におろした垂線の足をRとおく。楕円軌道に外接する半径\(a\)の円軌道(補助外接円)を設定し、中心をOとする。動径FPが近日点方向と為す角\(\theta\)を真近点角という。また、直線PRと補助外接円の交点をQ、直線QOと楕円軌道の交点をQ'と定める。このとき、角AOQを離心近点角\(E\)と呼ばれるもので、楕円軌道上の位置を指定するパラメータである。惑星の離心近点角を時間の関数として得られれば、任意の時点での惑星の位置を特定できるわけだ。惑星が円軌道を等速で運動していれば話は単純であるが、実際はそうではなく、楕円軌道上を焦点との距離によって速度を変えながら(面積速度を一定に保つように)運行していることが問題を複雑にしている。
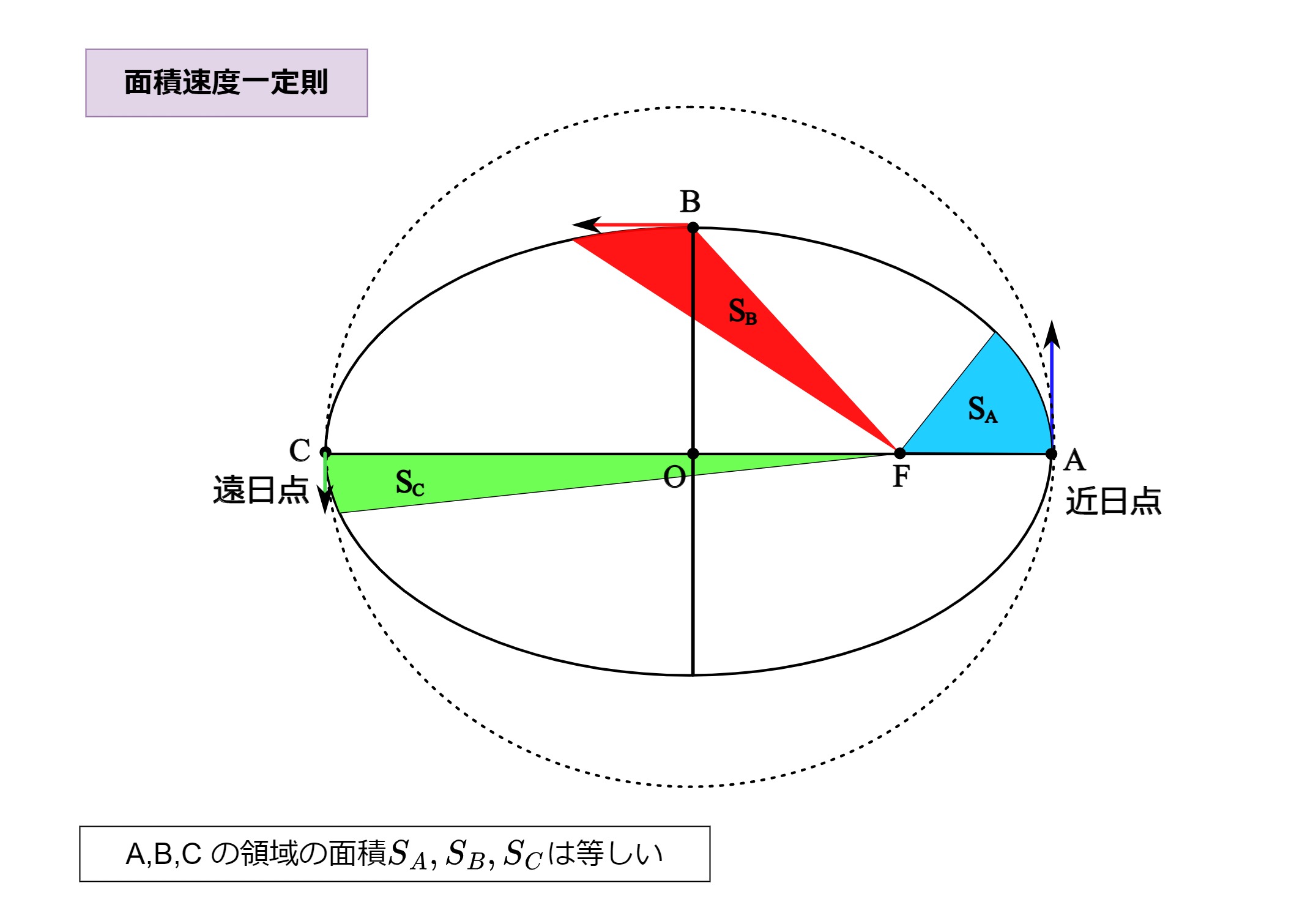
図2 面積速度一定の法則
図1.2に示すように、惑星はケプラーの第3法則(面積速度一定の法則)に従って、近日点近くでは速度が大きく、遠日点付近では速度が小さくなる。
いま、点Pの楕円運動の周期\(T\)で\(2\pi\)を除した量を平均運動\(n\)と定め、近日点を通過してからの時刻\(t\)について
\[M=n\,t\tag{1}\]
が成り立つように∠M=∠AOSをつくる。(点Sは、点Pと同じ周期だが外接円上を等速で運動する点であり、時間経過を代表する仮想的な運動点と考える。)このときの角\(M\)を平均近点角という。
図3
楕円軌道上の惑星(青点)の運動と外接円軌道上の平均運動(紫丸)の位置の時間変化
とにかく、Eは惑星の楕円軌道上の位置、Mは時間経過をそれぞれ表していると考えてよい。
図1.1の幾何学的関係から、楕円弧による扇形AFPの面積 \(\mathrm{{S}_{AFP}}\) は、図形AFQの面積 \(\mathrm{{S}_{AFQ}}\)の\(b/a\)倍となる。さらに、面積 \(\mathrm{{S}_{AFQ}}\)は、扇形面積\(\mathrm{{S}_{AOQ}}\)から三角形面積\(\rm{S}_{FOQ}\)を引いたものである。以上の関係を式で表現すると、
\[\mathrm{{S}_{AFP}}=\frac{b}{a}\mathrm{{S}_{AFQ}}=\frac{b}{a}\biggl(\mathrm{{S}_{AQ}}-\mathrm{{S}_{FOQ}}\biggr)\tag{2}\]
三角形FOQの面積は
\[\mathrm{S_{FOQ}}=\frac{1}{2}\mathrm{OF}\times\mathrm{QR}=\frac{ae\times a\sin{E}}{2}=\frac{a^2e\sin{E}}{2}\tag{3}\]
であり、扇形AOQの面積は
\[\mathrm{S_{AOQ}}=\pi a^2 \times \frac{E}{2\pi} =\frac{a^2 E}{2}\tag{4}\]
であるから、(3)、(4)を(2)に代入すると
\[\mathrm{S_{AFP}}=\frac{ab}{2}\left(E-e\sin{E}\right)\tag{5}\]
となる。一方、物理法則である面積速度一定の法則から、惑星の掃引する面積と時間について
\[\frac{\pi a b}{T}=\frac{\mathrm{S_{AFP}}}{t}\tag{6}\]
なる関係が成り立つ。(\(t\)は惑星が近日点から点Pに至るまでにかかる時間とする。)
(6)を(5)に代入して、平均運動\(n=2\pi/T\)を導入すると、
\begin{eqnarray}\frac{\pi a b}{T}&=&\frac{ab}{2t}\left(E-e\sin{E}\right)\\\\nt&=&E-e\sin{E}\tag{7}\end{eqnarray}
\(M=nt\)を代入すると
\[M=E-e\sin{E}\tag{8}\]
(8)式が今回アナログ計算機での解出を試みる非線形方程式、「ケプラー方程式」である。
この方程式を解き、離心近点離角E(惑星の楕円軌道上の点を指定するパラメータ)を平均近点角M(これの任意の時刻における値は容易に求まる)の関数として求めることで、任意の時刻での惑星の位置を決定することができる。だが、方程式の形を見ればわかるように、代数的・解析的変形では\(E\)について陽に解くことはできない。デジタル電子計算機による数値計算による方法のほかに、電子計算機発明以前であれば、級数を用いて近似解を得る方法、図的方法などが、現実的なケプラー方程式の解法であった。今回はアナログ電子計算機を用いて解のグラフ(E-Mグラフ)を得ることを試みる。
ケプラー方程式は超越関数を含む非線形方程式(超越方程式)であるが、アナログ電子計算機は超越関数を簡単に扱える特長があるので、好都合なのではないか、と考えた。ただし、微分方程式への変換が必要である。
2.アナログコンピュータプログラム
2.1 演算方程式
式(8)を常微分方程式に変換する。両辺を \(M(t)\) で微分すると
\begin{eqnarray}1&=&\frac{\mathrm{d}}{\mathrm{d}M}\left\{E-e\sin{E}\right\}\\\\&=&\frac{\mathrm{d}E}{\mathrm{d}M}\frac{\mathrm{d}}{\mathrm{d}E}\left\{E-e\sin{E}\right\}\\\\&=&\frac{\mathrm{d}E}{\mathrm{d}M}\left\{1-e\cos{E}\right\}\\\\\frac{\mathrm{d}E}{\mathrm{d}M}&=&\frac{1}{1-e\cos{E}}\tag{9}\end{eqnarray}
となる。(10)を、\(E(M=0)=0\) の初期条件のもと演算回路として構成すればケプラー方程式の解関数を得られるが、除算(逆数)回路が必要となり、結果としてダイナミックレンジが小さくなってしまう。
\(M\) は単調関数で、 \(1-e\cos{E}\neq{0}\) であるから、(9)は
\[\frac{\mathrm{d}M}{\mathrm{d}E}=1-e\cos{E}\tag{10}\]
と変形可能であり、\(E\) を独立変数として \(M(E=0)=0\) の初期条件のもと(10)の演算回路を組めば、除算なしで解き得る。求めたいものは \(E\) の \(M\) についてのグラフだが、単調性から、\(M(E)\)のグラフの変数軸を単に入れ替えることで \(E(M)\)グラフも求まる。上式右辺は適宜スケーリングすること。演算方程式は簡単なのでブロックダイヤグラムは省略する。
3.結果
低速モードの演算結果
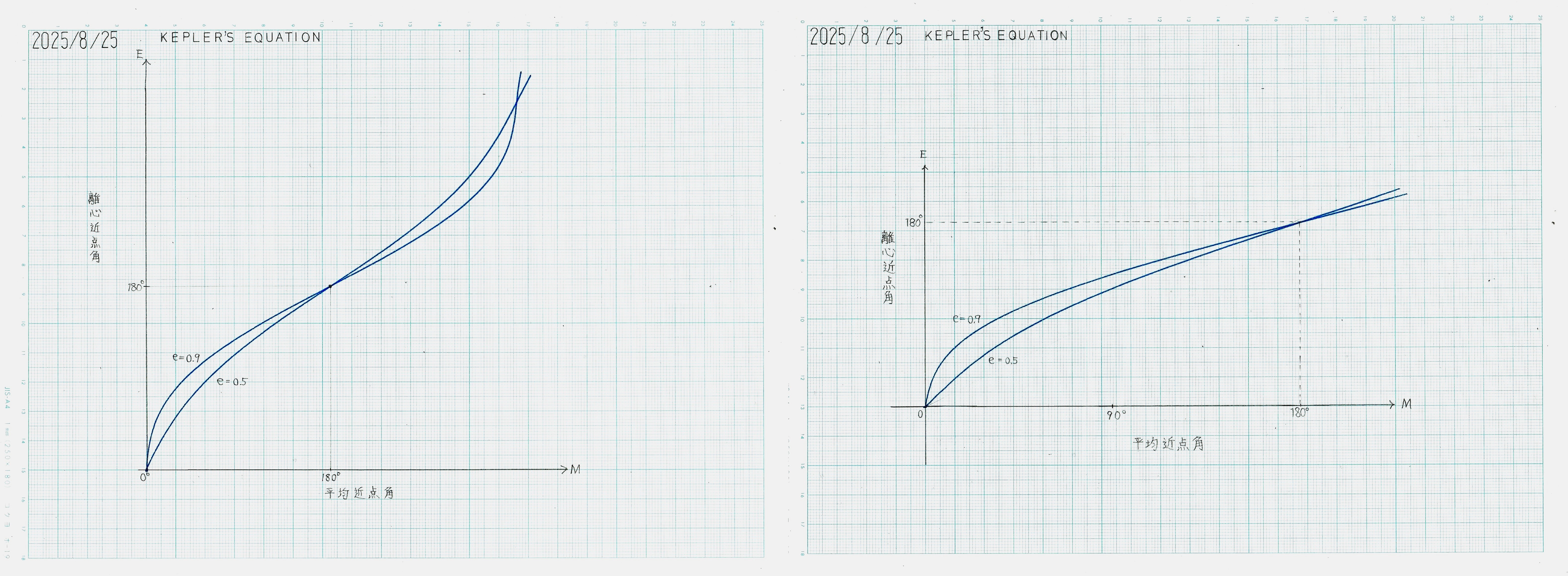
図4
Pythonで、ニュートン=ラフソン法による数値計算を行った結果を下図に示す。
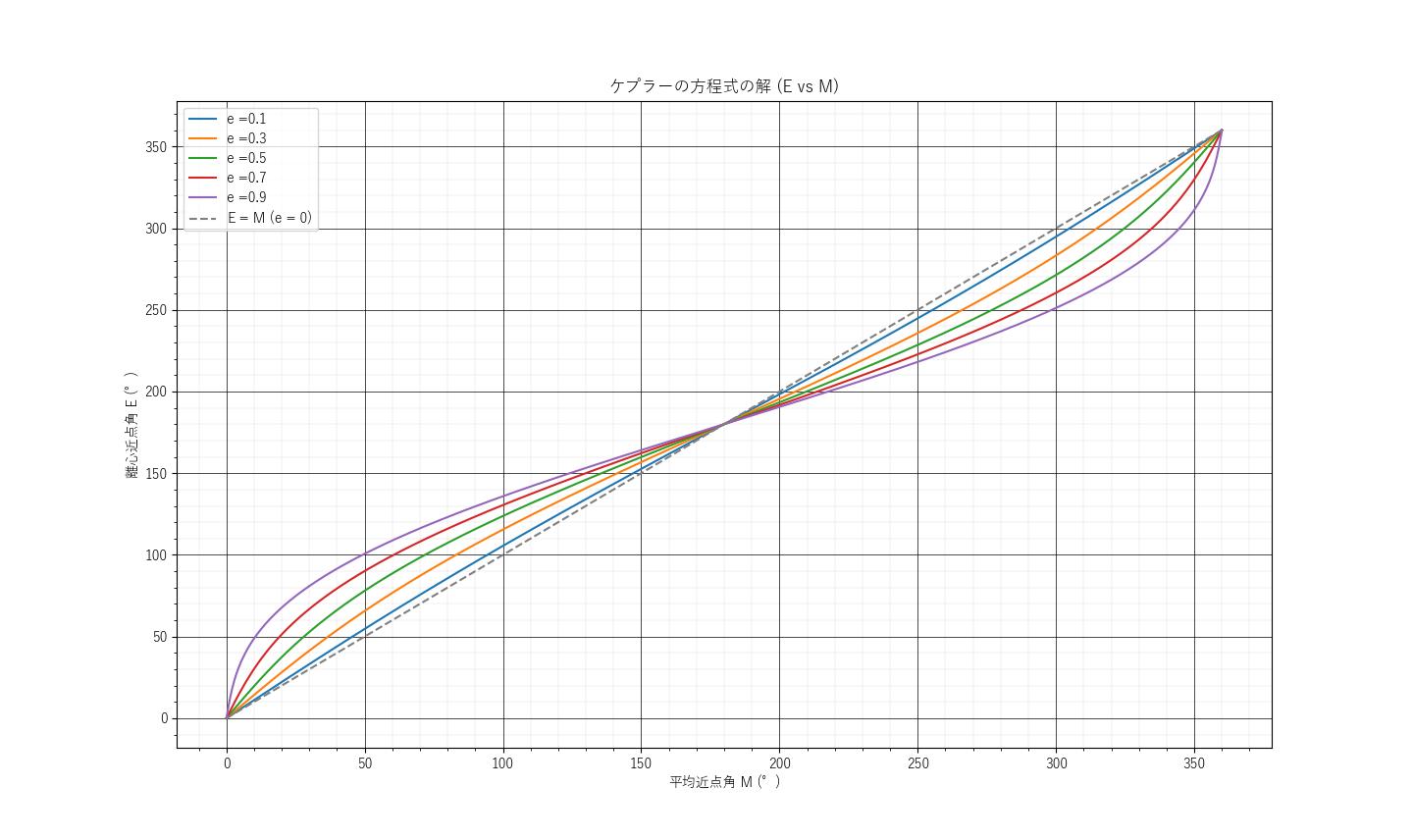
図5
0°から90°までを拡大した図 ↓
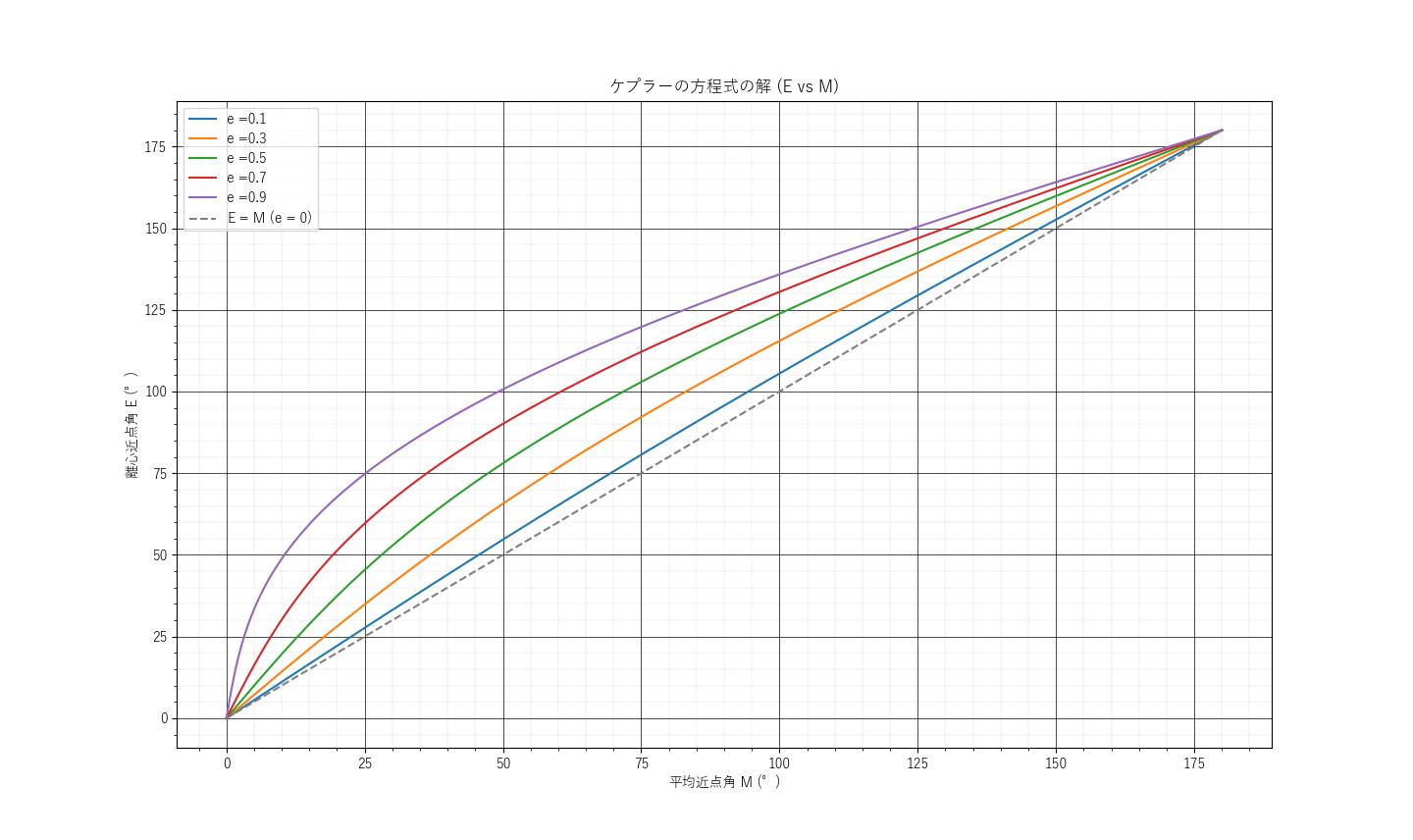
図6
4.参考文献
[1]FNの高校物理 「楕円軌道とケプラー方程式(Kepler equation)」http://fnorio.com/0158Kepler_equation/Kepler_equation.html(2025/8/14閲覧)
[2] Kiitire HURUKAWA, Fumihike IMAGAWA. (1967) "THE TABLE OF E-M IN KEPLER'S EQUATION."